Two Most Favorite Shapes Together
If p is the perimeter of an equilateral triangle inscribed in a circle, then what is the area of the circle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
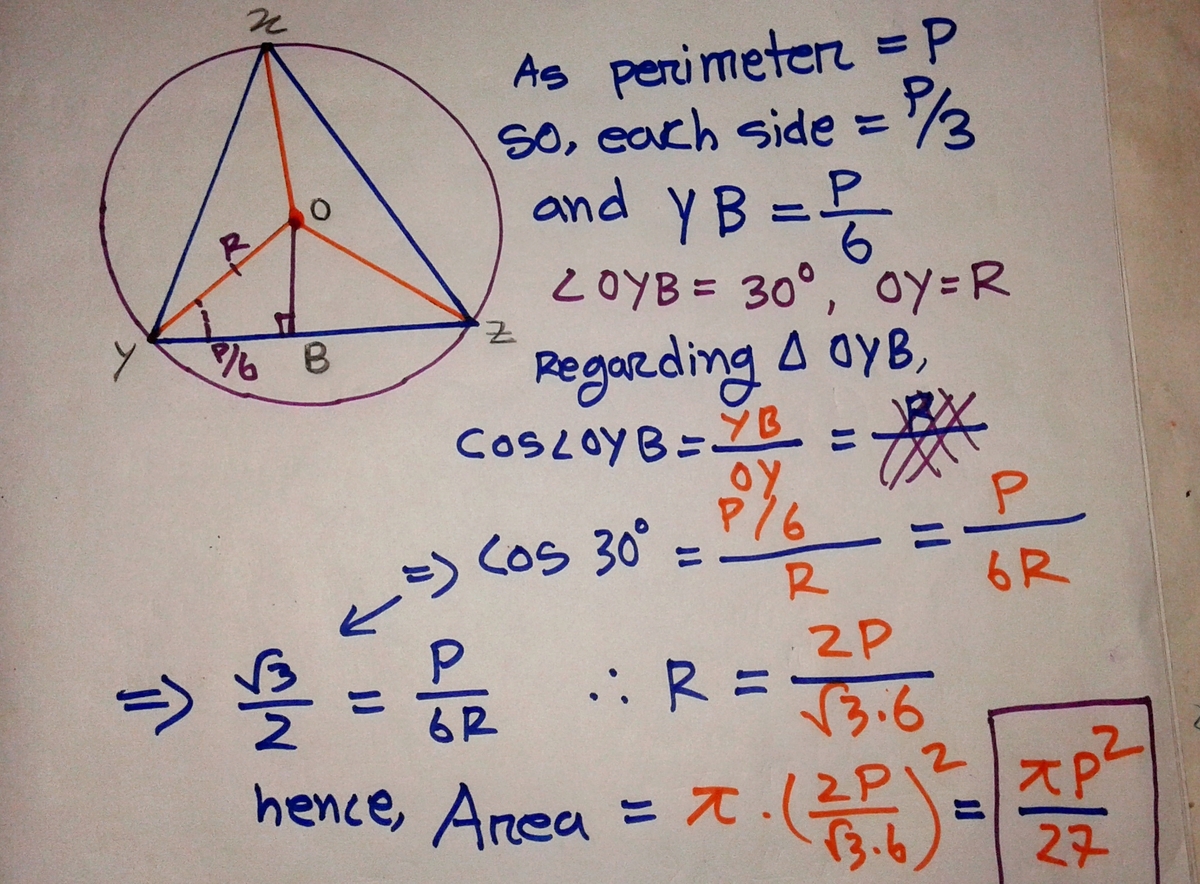
why the angle is 30 degree?
Log in to reply
He considered OY as an angle bisector
Log in to reply
So every angle bisector is 30 degree? Please explain me that.
Log in to reply
@Alex Vidal – As XYZ is an equilateral triangle.... so every angle of XYZ will be 6 0 ∘ . Thus, ∠ Y O Z will be 1 2 0 ∘ . Now consider triangle OYZ, which is an isosceles triangle, so ∠ O Y Z = ∠ O Z Y = 3 0 ∘ . Now I think, you should get it!
Why so colourful?
Log in to reply
Why not ! Isn't geometry colorful ? :)
Since, the perimeter is p , then the side of the equilateral triangle triangle is 3 p
now the altitude of the equilateral triangle is 2 3 * 3 p
the radius of the circle is 3 2 of the altitude of the equilateral triangle
i.e. 3 2 . 2 3 . 3 p = 3 3 p
area of the circle is π r 2 = 2 7 π p 2
Perimeter of the equilateral triangle =
p
.
So, its side =
3
p
Now we know that radius of the circumcircle of an equilateral triangle =
3
a
where
a
is side of the equilateral triangle.
So, for the given triangle, radius =
3
×
3
p
Now, area of a circle is
π
×
r
2
where
r
is the radius.
So, area of the required circle =
π
×
[
3
×
3
p
]
2
=
2
7
π
p
2
.
□
Moderator note:
Simple standard approach.
let M be the midpoint of XY and O be the centre of the circle.
OMX is a right angled triangle, whose hypotenuse is the radius, whose angle XOM is 60 degrees and whose longer short side is 6 P .
Easy trigonometry then gives the radius as
3 3 P
and so the area of the circle is 2 7 π P 2
If r is the radius of circle, then height h of triangle is 3r/2 as center of circle would divide height of triangle in 2:1 ratio. This can be shown by using the properties of similar triangle. If O is center and M is mid point of side YZ, then triangles OMY and XMY are similar. Therefore, OM/OY=YM/XY=1/2. OY=OX=r and h=XO+OM=3r/2. Pythagoras theorem on half triangle XMY, with sides p/3, p/6 and h, gives h^2=p^2/9 - p^2/36. As h=3r/2, we get 9r^2/4=p^2/12 or r ^2=p^2/27. Area of circle=πp^2/27.
Yes,that is correct!