Pulley on the way down
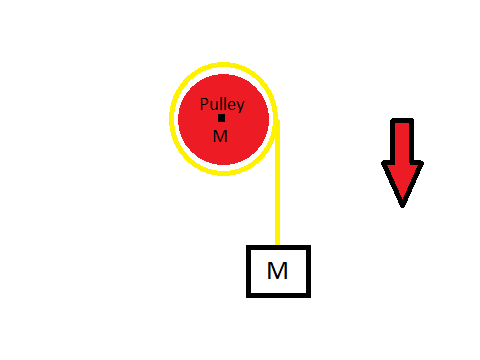
A rope is wound round a pulley of mass M and its free end is attached to a mass M which is pulled down by gravity. At time t = 0 , the block is set free and begins to drop.
Find the acceleration of the block, a .
Details and Assumptions:
- The rope does not slip and is massless.
- If your answer is in the form of B A g , where A and B are coprime positive integers, find A + B .
- g = 1 0 m / s 2 .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions

You can check out one of my other problems.. 😊 its named "I <3 pulleys"
Log in to reply
Solved that one too. Nice one
Nice application of concepts
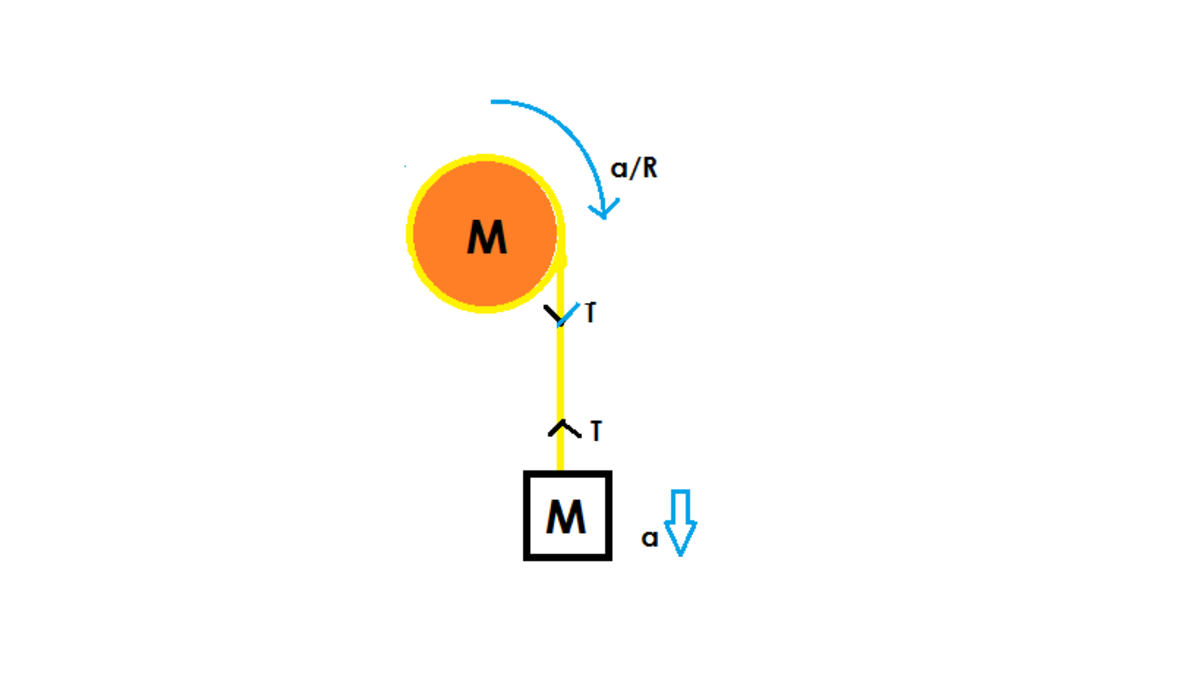 Here the rope does not slip on the pulley and hence the angular acceleration of the pulley is equal to:
\
α
=
R
a
(
1
)
Now, we write equations for the pulley and the block.
For the block we have,
M
g
−
T
=
M
a
(
2
)
For the pulley,
T
R
=
2
M
R
2
×
α
(
3
)
Substituting value of
α
from equation (1), we get
T
R
T
=
2
M
R
2
×
R
a
=
2
M
a
(
4
)
(
)
Adding equation (2) and (4), We get
M
g
−
2
M
a
a
=
3
2
g
=
M
a
Here the rope does not slip on the pulley and hence the angular acceleration of the pulley is equal to:
\
α
=
R
a
(
1
)
Now, we write equations for the pulley and the block.
For the block we have,
M
g
−
T
=
M
a
(
2
)
For the pulley,
T
R
=
2
M
R
2
×
α
(
3
)
Substituting value of
α
from equation (1), we get
T
R
T
=
2
M
R
2
×
R
a
=
2
M
a
(
4
)
(
)
Adding equation (2) and (4), We get
M
g
−
2
M
a
a
=
3
2
g
=
M
a
Very clear argument, great writeup, and a diagram!
Log in to reply
Thanks @Josh Silverman
Exactly! +1
Log in to reply
Thanks bro and for liking the solution
oye meri problem bi kar lo bhai !
sir, there was a problem posted by me called advaced ? really ?? i am not able to find it ! plz help ! @Josh Silverman
Log in to reply
it was a nice problem !
@shubham dhull This is not the place to do this.
Log in to reply
@Josh Silverman – then when should i ask you sir ? it was a nice problem ! plz tell
why is this problem level 3 it should be 1 .
The problem is very easy but the solution by Steven Chase is very conceptual.