Newtons Inverse Roots?
If r 1 , r 2 , r 3 , r 4 , r 5 are the complex roots of the equation x 5 − 3 x 4 − 1 = 0 . Find the value of r 1 9 1 + r 2 9 1 + r 3 9 1 + r 4 9 1 + r 5 9 1 .
The answer is -27.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Wow, nice solution. Didn't think that the same methods would apply here due to the differences in powers .
Log in to reply
Newton's sums still work, though!
great solution
It can be solved using Newton Sum method.
Let:
S 1 = i = 1 ∑ 5 r i 1 = 1 ∑ 5 r 1 r 2 r 3 r 4 r 5 r i r j r k r l = 0
S 2 = 1 ∑ 5 r i r j 1 = 1 ∑ 5 ( r 1 r 2 r 3 r 4 r 5 ) 2 r i r j r k = 0
S 3 = 1 ∑ 5 r i r j r k 1 = 1 ∑ 5 ( r 1 r 2 r 3 r 4 r 5 ) 3 r i r j = 0
S 4 = 1 ∑ 5 r i r j r k r l 1 = 1 ∑ 5 ( r 1 r 2 r 3 r 4 r 5 ) 4 r i = 1 3 = 3
S 5 = r 1 r 2 r 3 r 4 r 5 1 = 1 1 = 1
And let: P n = r 1 n 1 + r 2 n 1 + r 3 n 1 + r 4 n 1 + r 5 n 1
Then:
P 9 = S 1 P 8 − S 2 P 7 + S 3 P 6 − S 4 P 5 + S 5 P 4 = 0 − 0 + 0 − 3 P 5 + P 4 = − 3 ( − S 4 P 1 + 5 S 5 ) + ( − 4 S 4 ) = − 3 ( − S 4 S 1 + 5 S 5 ) − 4 S 4 = − 3 ( − S 4 ( 0 ) + 5 ( 1 ) ) − 4 ( 3 ) = − 1 5 − 1 2 = − 2 7
While the solution seems to be difficult but it can be readily calculated with a spreadsheet for any P n (see below):
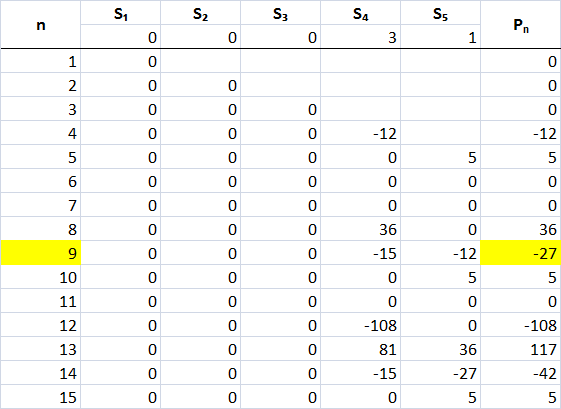
NICE ARRAY. Did you make that using Excel? and does S 4 denote the term in Newton's sums? Because S 4 and S 5 should be constant alone.
Log in to reply
Yes, it is Excel. It is easy. Yes, usually S 4 = ∑ 1 5 a i a j a k a l , here it is S 4 = ∑ 1 5 a i a j a k a l 1 . And S 5 = a 1 a 2 a 3 a 4 a 5 1 . The rest works exactly the same using Newton Sum. You can use the same array for all similar problem.
To make this simpler, we can let x = 1/ y,
We should have y^5 + 3 y - 1 = 0 and its roots shall be inverse of roots to x^5 - 3 x^4 - 1 = 0, which can save from finding inverse for sum required.
I find myself easier to solve using programmed solver rather than doing arithmetic of relating power 1 to power 9 using traditional mathematics.
0.331989029584509
0.839072433066608 + j 0.943851550132862
0.839072433066607 - j 0.943851550132862
-1.005066947858860 + j 0.937259156692892
-1.005066947858860 - j 0.937259156692892
After taking a power of 9 to each and every root,
4.89907E-05
2.077749665 + j 7.902869758
2.077749665 - j 7.902869758
-15.57777416 + j 7.939064242
-15.57777416 - j 7.939064242
Sum up to -27 + j 0 = -27
Trevor Arashiro don't you think you must correct the Language of the question? Complex roots occur in pairs!
Real numbers are also complex. For example, 5 can be written as 5 + 0 i .
Log in to reply
(no offence) i said complex ROOTS. while typing i was thinking this only. But Complex roots occurs in a pair! and no denying in 5=5+0i
Log in to reply
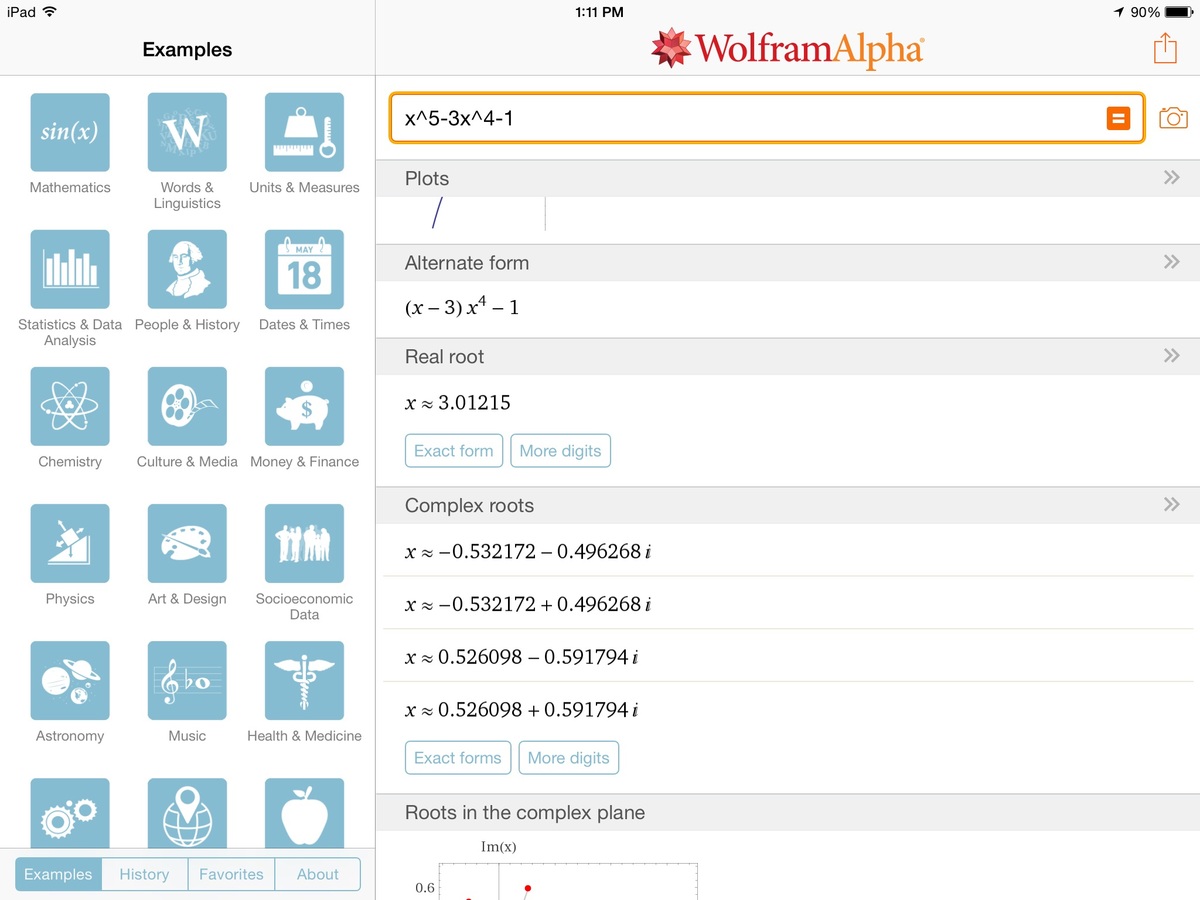
3.01 is technically a complex root. And it does have a pair. 3 . 0 1 ± 0 i
Log in to reply
@Trevor Arashiro – You saying of Wolfram Alpha? Haha... don't mind but sometimes it is damn wrong. I will tell you later (after posting my first question). Till then: complex root a+ib where b isn't zero. Now posting my question----->
@Trevor Arashiro – Solve the Integral Integration i have created! then see the answer on WolframAlpha!
Hint: find r 1 9 + r 2 9 + r 3 9 + r 4 9 + r 5 9 of the equation x 5 + 3 x − 1
This note explains why you have to reverse the coefficients of a function to get the inverse of the roots (by inverse I mean if it has a root c, the inverse is c 1 )
Ok, solution below
Let a = r 1 , b = r 2 . . . e = r 5
Define P n = a n + b n + c n + d n + e n and
S 1 = a + b + c + d + e
S 2 = a b + a c + a d + a e + b c + b d + b e + c d + c e + d e . . .
.
.
.
S 5 = a b c d e
Or more specifically, S n = the nth symmetric sum
We will be working with the equation x 5 + 3 x − 1 = 0
for reasons mentioned above
By newtons sums, we meed to find
P 9 = P 8 S 1 − P 7 S 2 + P 6 S 3 − P 5 S 4 + P 4 S 5
However, by vieta's, note that S 1 = S 2 = S 3 = 0 and S 4 = 3 and S 5 = 1 therefore (I will substitute theft values from now on), the above simplifies to
P 9 = − 3 P 5 + P 4
We need to solve for P 5 and P 4
P 4 = − 4 S 4 ⇒ − 1 2
(Note: the lack of the first few terms in the previous and the next is due to S 1 = S 2 = S 3 = 0 ).
P 5 = − P 1 S 4 + 5 S 5 ⇒ − 3 P 1 + 5
Now, P 1 = a 1 + b 1 + c 1 + d 1 + e 1 and S 1 = a + b + c + d + e = 0
Therefore, P 1 = S 1 = 0
Plugging this value in to our equation above
P 5 = − 3 P 1 + 5 = − 3 ( 0 ) + 5 = 5
We have now established
P 5 = 5 , P 4 = − 1 2 , S 4 = 3 , S 5 = 1
Plugging these into our first equation.
P 9 = − ( 3 ) ( 5 ) + ( 1 ) ( − 1 2 ) = − 2 7
I will emulate the solutions posted on the linked problem, which use Vieta's.
From the given polynomial, we have
∑ r i = 3
and
∑ r i − 1 = 0 .
The sum of the reciprocals of the roots come from the fact that the polynomial with reciprocal roots has its coefficients reversed.
x 5 − 3 x 4 − 1 x 4 ( x − 3 ) x 4 x − 9 ∑ r i − 9 = 0 = 1 = ( x − 3 ) − 1 = x ( x − 3 ) 2 = ∑ r i ( r i − 3 ) 2 = ∑ r i r i 2 − 6 r i + 9 = ∑ r i − 6 + 9 r i − 1 = ∑ r i − ∑ 6 + 9 ∑ r i − 1 = 3 − 5 ( 6 ) + 0 = − 2 7 .