A problem in honour of solving 1000 problems
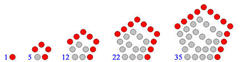 Is 1001 a pentagonal number?
Is 1001 a pentagonal number?
Note: If yes, then enter the term number of 1001 in the sequence of pentagonal numbers as your answer. For example, the term number of 12 is 3, so you will enter the answer as 3; If no, then enter the answer as 1001.
Bonus question : How will you find whether a number is a pentagonal number or not? Is there any test?
The answer is 26.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
The simplest way to test whether a positive integer x is a pentagonal number is :
n = 6 2 4 x + 1 + 1
If n is a natural number , then x is the n t h pentagonal number.
Here x = 1 0 0 1 , we get :
n = 6 2 4 ( 1 0 0 1 ) + 1 + 1 ⇒ n = 6 2 4 0 2 4 + 1 + 1 ⇒ n = 6 2 4 0 2 5 + 1 ⇒ n = 6 1 5 5 + 1 ⇒ n = 6 1 5 6 ⇒ n = 2 6
Moderator note:
This solution is incomplete. Where did you get the formula n = 6 2 4 x + 1 + 1 ?
Here's how we get this:
Note that the series for the pentagonal numbers obeys the following recurrence:
T n + 1 − T n = 4 + 3 ( n − 1 ) = 1 + 3 n ∀ n ≥ 1 ; T 1 = 1
This recurrence can be solved by "piling up the differences between terms" as follows:
T n = i = 0 ∑ n − 1 ( 1 + 3 i ) = n + 3 ⋅ i = 1 ∑ n ( i − 1 ) = n ( 1 + 2 3 ( n − 1 ) ) ∀ n ≥ 1
Now, let x ≥ 1 be a number selected for testing. We form a "testing method" using the closed form for T n obtained.
T n = x ⟹ 2 x = 2 n + 3 n 2 − 3 n = 3 n 2 − n ⟹ 3 n 2 − n − 2 x = 0
Using the quadratic formula, one gets,
n = 6 1 ± 1 + 2 4 x
But, we need value of n to be ≥ 1 to test whether it is in the sequence or not and values of n obtained that are < 1 are just extraneous solutions. So, our required "testing value" is,
n = 6 1 + 1 + 2 4 x
We have our "testing method" ready and it is now obvious from the result obtained that,
n ∈ Z + ⟺ x is a pentagonal number.
Log in to reply
I Can't understand your "piling up the differences between the terms".
Log in to reply
By "difference", I mean the f ( n ) in T n + 1 − T n = f ( n ) , i.e., the variable difference between the terms. When I say "piling up the differences", I'm just saying that we sum up these variable differences up to get the closed form. Here's a simple demonstration as to how the summing method works :
We have the base cases T 0 = 0 and T 1 = 1 by definition and the following recurrence ∀ n ≥ 1 :
T n + 1 − T n = 1 + 3 n ⟹ T n + 1 = 1 + 3 n + T n ⟹ T n + 1 = ( 1 + 3 n ) + ( 1 + 3 ( n − 1 ) ) + T n − 1 ⋮ ⟹ T n + 1 = ( 1 + 3 n ) + ( 1 + 3 ( n − 1 ) ) + … + ( 1 + 3 ( n − n ) ) + = 0 T 0 ⟹ T n + 1 = i = 0 ∑ n ( 1 + 3 i ) ⟹ T n = i = 0 ∑ n − 1 ( 1 + 3 i ) ∀ n ≥ 1
P.S - Thanks to you, I noticed a minor typo that was in my comment. Fixed it just now. :)
It can be derived easily as the nth pentagular number is sum of first n numbers of the series 1,4,7,10...........
Yes. Simple Plug and Check :3
Log in to reply
Cheers! xD
Log in to reply
Yeah! Cheers! xD
Log in to reply
@Mehul Arora – crap made a mistake of division. Hahahaha
Log in to reply
@A Former Brilliant Member – Bhai hota hai kabhi kabhi .. xD
This question works for me too.See my profile this was my 1000th question too .
Log in to reply
Then , you can post another problem...
A method my 8th grade mathcounts teacher taught me is that pentagonal, triangonal, etc. numbers can be approximated with a combination of a square and triangles.
A triangular number is n ( n − 1 ) / 2 A square is n 2
Thus a pentagonal number would be n 2 + n ( n − 1 ) / 2 . Much easier than memorizing formulas, right?!
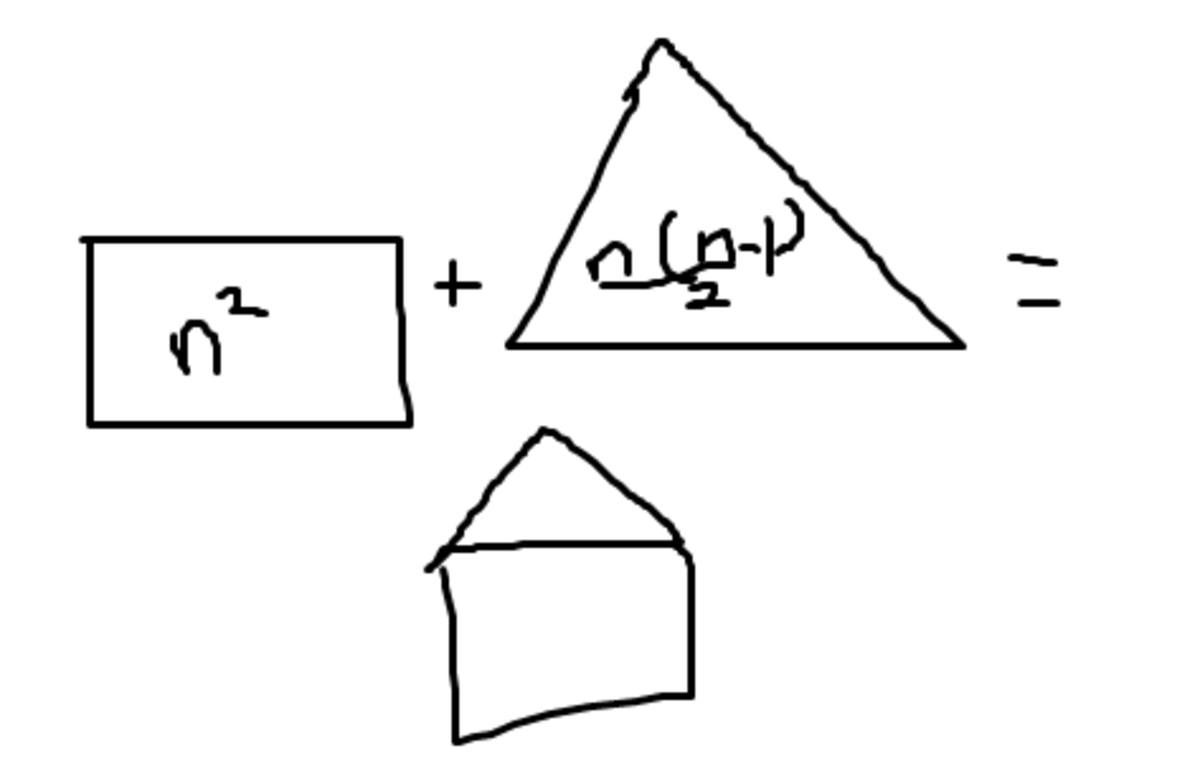
And n=26.
The Expression for the nth pentagonal number is n(3n-1)/2,
Equate n(3n-1)/2 = 1001 and this gives us the quadratic equation:
3n^2 - n - 2002 = 0
Solver for n
3n^2 - 78n + 77n - 2002 = 0
3n(n-26) + 77(n-26) = 0
(3n + 77)(n -26) = 0
The only solution permissible is n = 26
This is a pretty easy way to do it too, provided that the number is not enormous.
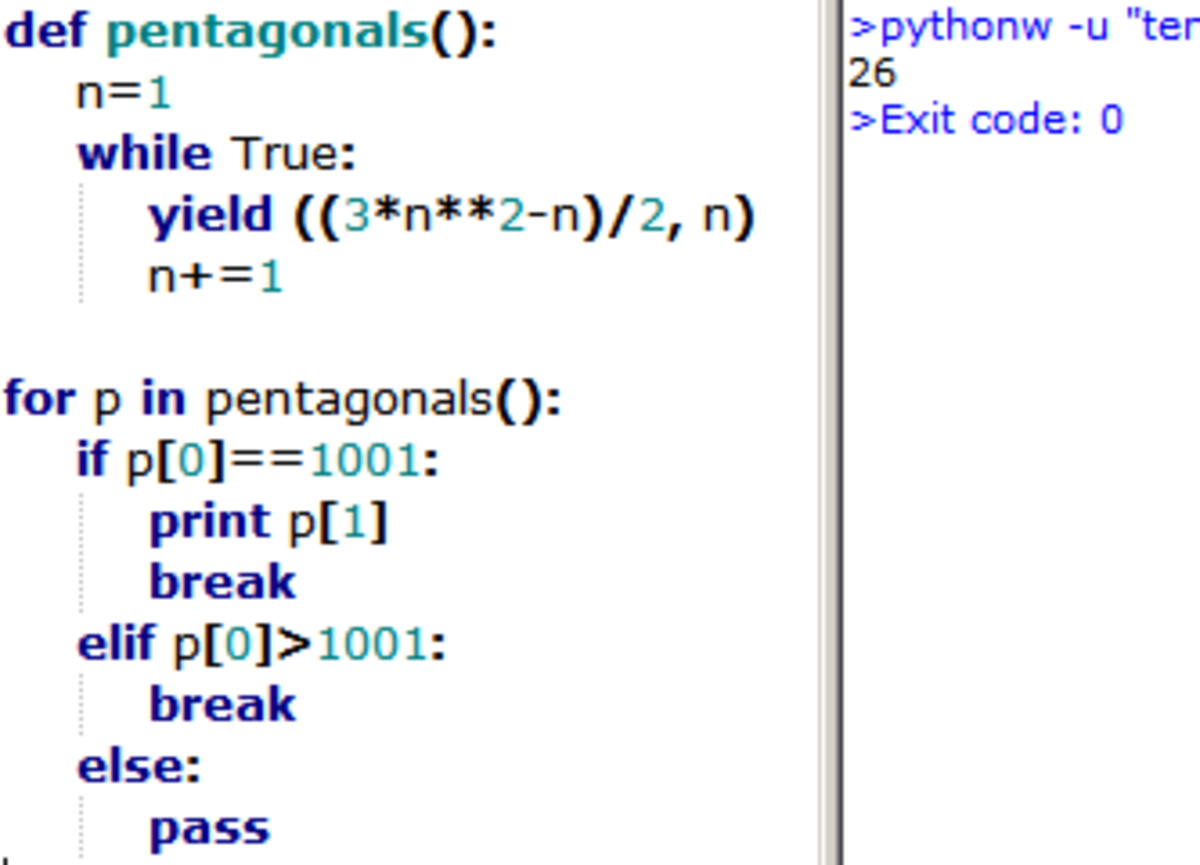
Incidentally the formula used in this script and that test are both provided in wikipedia.
Note that 1 = 1 , 5 = 1 + 4 , 1 2 = 1 + 4 + 7 etc. So these numbers are in the form of 3 n − 2 .
A sum of an arithmetic progression is the (average of the first and last number) times (number of terms)
(example 1 + 2 + 3 . . . + 9 = ( 1 + 9 ) / 2 × 9 = 4 5 )
This can be rearranged to form (first term + last term) times (number of terms divided by 2)
Therefore, since each term of a pentagonal number is 3 n − 2 , a pentagonal number is in the form of ( 1 + 3 n − 2 ) × 2 n =
= 2 n ( 3 n − 1 )
Checking, we prove by induction
Base case n = 1 : 2 1 × 2 = 1 . Therefore n=1 is true
the last term on the LHS is 3 n − 2 . Therefore the next term is 3 ( n + 1 ) − 2 = 3 n + 1 .
Using the inductive hypothesis, we add 3 n + 1 to the RHS
= 2 n ( 3 n − 1 ) + 3 n + 1
= 2 n ( 3 n − 1 ) + 2 6 n + 2 = 2 3 n 2 − n + 6 n + 2 = 2 3 n 2 + 5 n + 2
Using Null Factor Law, n = − 1 makes this expression = 0 , so we can factorise it with one of it's factors being n + 1
= 2 ( n + 1 ) ( 3 n + 2 ) = 2 ( n + 1 ) [ 3 ( n + 1 ) − 1 ]
Since n + 1 is true, and n = 1 is true, this formula works.
Solving,
2 n ( 3 n − 1 ) = 1 0 0 1
3 n 2 − n − 2 0 0 2 = 0
n = 2 a − b ± b 2 − 4 a c
n = 6 1 ± 1 + 2 4 0 2 4
n = 6 1 ± 1 5 5
= 6 1 5 6 = 2 6 (The other solution − 1 5 4 / 6 is negative and not needed)
thanks for the solution. it helped me understand this problem more. :)
It can be seen that
- term 1 -> 1+0+0
- term 2 -> 2+1+1
- term 3 -> 3+2+2
- term 4 -> 4+3+3
- term 5 -> 5+4+4
-
term 6 -> 6+5+5
So
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
|
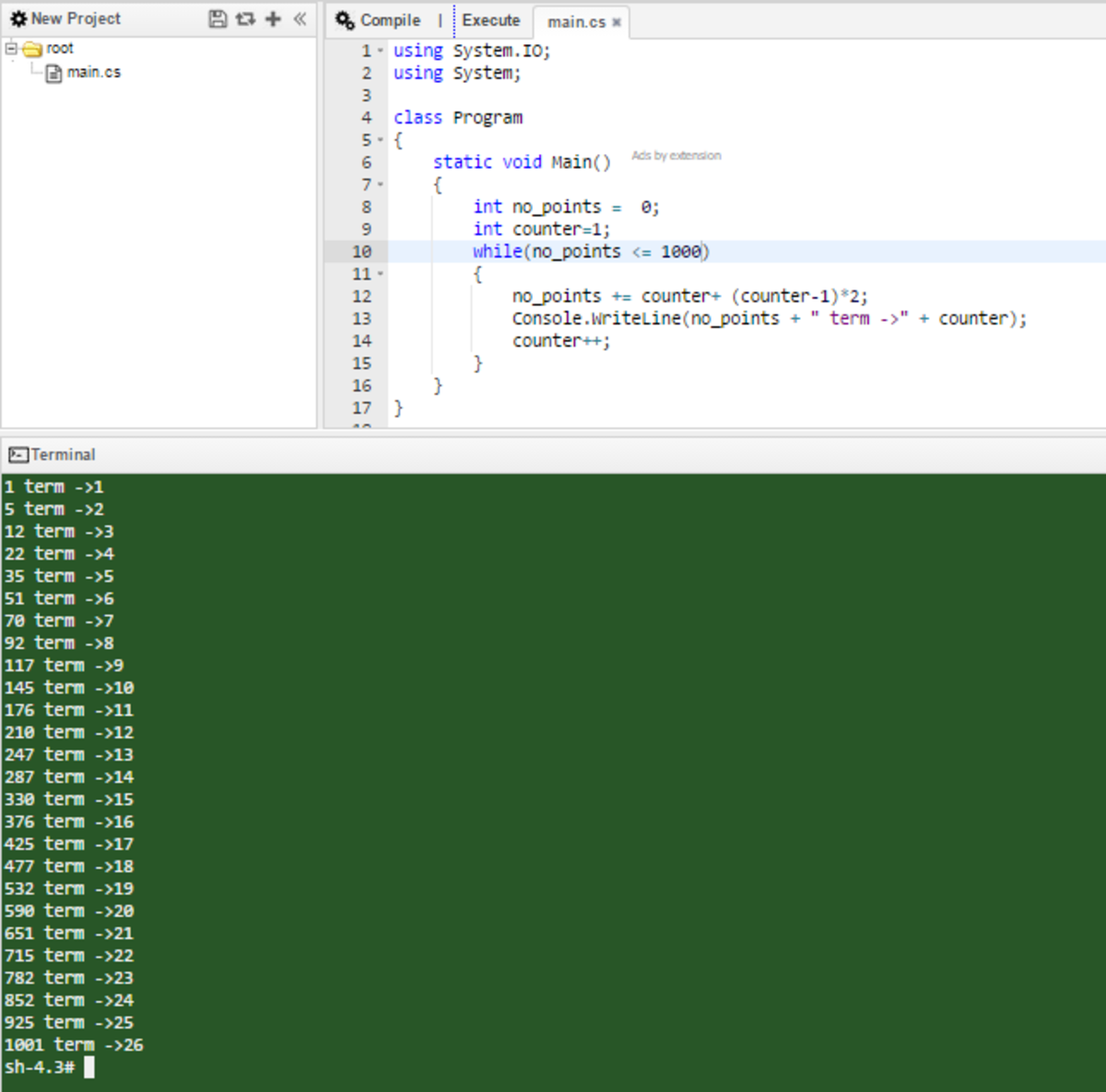
Pattern of 1, 5, 12, 22, 35, 51 -> Formula of sequence is (n*(3n-1))/2. Therefore, 3n^2-n-2002 = 1001, n = 26.
I did this by figuring out how much each pentagonal number increases each time. Assuming the first picture is n = 1
Every time, 3 new lines are added of size n, but because of corners, 2 are counted twice.
Therefore, we can say that n * 3 - 2 dots are added each time. (Ex. For the first case, 1 * 3 -2 = 1 dot is added to 0)
However, n* 3 - 2 is neither a geometric nor arithmetic sequence. However, by splitting it up, you can make it both. In other words, counting the total number of ns given by each part of the equation. (pretty proud of thinking of this) Now the problem becomes easy. First, the -2 term. At any n, the - 2 part of the equation will have taken 2n dots total.
For the 3x, it gets a bit more complex, because you can't just multiply by x, so instead, find the average of all terms. A good way of doing this is adding the first and last term, than dividing by 2. (3+3x)/2. Finally, multiply again by x (average * number of terms = total), and add it back to the other formula and you'll get
(3x+3x^2)/2-2x; or x(1.5x-3.5) if you like it that way.
Now it's simply a matter of plugging in integers (which is what I did) or setting it equal to 1001 and using algebra (which I guess is the 'smart' way), and you'll find that, for x = 26, y = 1001.
p(n) = p(n-1) + 3(n-1) + 1
=> p(n) = (3n^2 - n)/2
(3n^2 - n)/2 = 1001 (quadratic equation solved)
n = 26
x is pentagonal number if and only if
there is a positive integer n with satisfies (3n^2 - n)/2 = x
The sequence proceeds as 1, 5, 12, 22, 35, between each term the differences proceed as 4, 7, 10, 13 and the difference is permanently 3, so we can deduce this must be based around square numbers. so we take 1^2 + 0 = 1, 2^2 +1 = 5, 3^2 +3 = 12, as you can see the term added is a triangle number, so the formula we use for this is ((n-1)^2+(n-1))/2 , so the formula we get for pentagonal numbers is n^2 +((n-1)^2 +(n-1))/2, which is simplified to n ( 3n -1 ) /2. Then we can form the equation n ( 3n -1 ) /2 = 1001, then you solve the equation to get n = 26
i come to two different methods to solve this: the pentagonal number of n equals either \sum {n}^2n-1 or n^2 + \sum {i=1}^n-1
we know that any sum from 1 to any value equals half the square of n plus half the value of n, allowing us to get the formula
P= n^2 + ( (n-1)^2 + n-1) / 2
or
P=n^2 + n*(n-1)/2
therefore P= 3(n^2)/2 - n/2
Solved exactly like Prasun Biswas, except that I took P(n) - P(n-1) = 3n-2
P(n) be the 'n'th pentagon number then its easily noticed that P(n) = (3n-2) + P(n-1)
the difference d is 4+3(n-1) by putting this value in equation an=a1+(n-1)d the ans is 26
You can notice that every pentagonal number includes the privious one but you add a certan number So I wrote it as a sequence (1, 4, 7, 10...) [notice that 5=4+1 , 12=7+5] So we can concloude that any pentagonal number equals the sum off all n terms before it Using the rule sn=n/2 (2a+d (n-1)) , 1001=n/2(2+3 (n-1)), 3n^2-n-2002=0, n= 26 or n=-77/3, n=26