A Quadrilateral in a Square
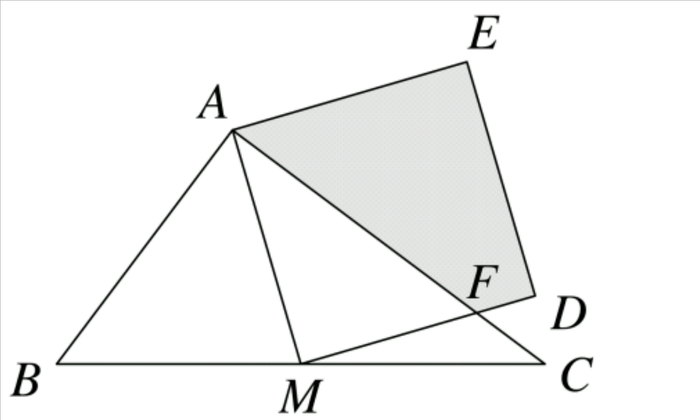 Let ABC be a triangle such that AB = 6, AC = 8 and BC = 10. Let M be the midpoint of BC. Draw Square AMDE as above, and let MD intersect AC at F.
Let ABC be a triangle such that AB = 6, AC = 8 and BC = 10. Let M be the midpoint of BC. Draw Square AMDE as above, and let MD intersect AC at F.
Find the area of quadrilateral AFDE.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
16 solutions
How can triangle ABC be a rectangle?
Log in to reply
triangle ABC has sides 6, 8, 10
if you try these in the pythagorean theorem you will see that they satisfy it…
(a^2) +(b^2)=c^2 // (6^2)+(8^2)=10^2 // 36 + 64 = 100 = TRUE
therefore ABC is a right angle
triangle ABC is a rectangle?
Elegant solution
Log in to reply
use the median property as taught in solution of triangle where 2*(median^2 + a^2/2) = c^2 + b^2
What if the triangle was not a right angle : Lengths 8, 10, 12 for example
Log in to reply
I still can solve it but the solution is not beautiful, do you have an elegant solution for this case too?
Log in to reply
This problem is posted in a competition named Knagaroo where you have to do each problem in less than 3 minutes. That's why there exist an elegant solution. If the triangle was diferent like in your example , the lenght of AM, wouldn't be that clear and such an elegant soluiton wouldn't exist.
Pythagoras theorem is does not apply in this triangle my dear Jordi
Log in to reply
deva this is height of foolishness
Triangle ABC comes out to be a right angled triangle, he has used converse of Pythagoras theorem for this.
Yes it does
yes it does along with trigonometry, with the ratio of the three sides of triangle ABC, the 3, 4, and 5 ratio is a standard right angled triangle with angle BAC as the 90 degrees;m<DFC = m<BAM = m<FAE=m<AFM; <E = <D = 90 degrees. BM =MC = 5. LOL how am I doing so far..
By the way, this problem is from the Kangaroo of this year
Log in to reply
This was an interesting problem so i decided to post it @Jordi Bosch
Log in to reply
That's fine!!! I enjoied solving it
Log in to reply
@Jordi Bosch – I am amazed nobody saw the cosine law in the question.
Nice solution
Nice solution
pythogoras! intersting
Nice solution
Awesome.... Man..... :)
nice.. So there is solution by not using cosine law
but here u find out a area of AMF NOT find out a area of aedf
Log in to reply
Thats because AEDM is a square and if we want to fins the area of AEFD we are able to do: [AEFD] =[AEDM]-[AFM]
I find it to be approximately 124/8 = 15.5
how do you get AM / MF = AC / BA ?? what is this theorem ? I am little bit out of date :P
Log in to reply
I apply Thales thorem; it says if two triangles are similar, there exist a proportion between the sides. Check it out:
Good . Nice rational thinking problem andsolved fine by Jordi.
In my idiom, (catalan), we say it this way, I think in English would be a right angled triangle.
Triangle ABC is a rectangle? Or do you mean a right triangle ?
Log in to reply
right triangle is half the rectangle.... though, it bumped me as well....
dude triangle AMB cannot be an isosceles triangle. for the simple reason that angle AMB will be 90 if u say so that it is isosceles, and angle AMC is also 90 because all sides of a square are 90 degree angles. which is not possible because angles AMB+AMD+DMC=180 and not angles AMB+AMD=180 therefore AM cannot equal to 5 cm
The correct answer is 124.7392/8 the area is 15.5924
Using Stewart's theorem
10d^2 + 25 10 = 8^2 5 + 6^2*5 10d^2 + 250 = 320 + 180 10d^2 = 320 + 180 - 250 10d^2 = 500 - 250 10d^2 = 250 d^2 = 25 d = 5
Since the triangle is a right triangle : 6 - 8 - 10
AM/MF = AC/AB 5/MF = 8/6 MF = 30/8 = 15/4
Area of Triangle [AMC] =1/2 [(15/4)(5)] = 75/8 Area of Square [AMED] = 25
Area [ AFDE] = 25 - 75/8 = 125/8 cm^2
Log in to reply
Yay but Stewarts theorem is kind of difficult to remember
We are not given that the triangle ABC is inscribed in a circle, so we cannot assume so. We could instead use the trigonometry of the right-angle triangle BAC to find the angle ABC and then cosine law to find AM.
Log in to reply
Not but every right angle can be inscribed in a semicircumference, so you can add it to the diagram without any problem
Every right angled triangle can be considered to be inscribed in a semicircle, with diagonal as the diameter.
Atlast someone saw this All other solutions inscribed the triangle in a circle
Why did you use Pythagorean theorem? Is triangle ABC a right triangle?
Log in to reply
Yes, the converse of Pytagoras theorem tells us that if we have a triplet af numbers (a,b,c) that satisy a 2 + b 2 = c 2 , the triangle with a,b,c as a sides is a right angle. In this case (6,8,10) satisfy it
Yes, because we drew a square AMDE per the problem definition.
Log in to reply
Oops, sorry, I thought you meant triangle AMF, my mistake.
we know that, In right triangle hypotenuse^2=base^2+Orthogonal^2 here,bc^2=ab^2+ac^2 so,abc right triangle
what is the formula of this?
The cosine rule can also be used to find AM cos θ = 2 ∗ a ∗ b a 2 + b 2 − c 2 1 0 6 = 2 ∗ 6 ∗ 5 6 2 + 5 2 − c 2 1 0 6 ∗ 6 0 = 3 6 + 2 5 − c 2 c 2 = 2 5 c = 5 The rest is quite simple
@Jordi Bosch great solution
I solved it in a complicated way but this solution is very simple and I believe that simplicity is the beauty
Can you do cosign without a calculator ? If so - How ?
Yay that's a good way to find AM quicly also
(I.) The angle BAC is a right angle.
Proof:
10, 8 and 6 are a Pythagorean triple (multiples of the primitive (5,4,3)) therefore the triangle ABC is a right triangle. The right angle is the one opposite from the hypotenuse.
(II.) Draw a segment MK which is perpendicular to AC (not shown). Then the triangles KMC and ABC are similar (and KM=3)
Proof:
AB and MK are both perpendicular to AC; therefore they are parallel to each other. Hence, the angles ABC and KMC are equal. The triangles ABC and KMC share three angles, therefore they are similar. As AB=2MC by definition, the ratio is 2. Therefore KM=AB/2 =3
(III.) AM=5
Proof:
The triangles KMA and KMC share a side (KM); AK=KC from the similarity of ABC and KMC; both angles MKA and MKC are right angles by construction. Therefore the triangles are equal and AM-MC=5
(IV.) 3AF = 5MF
Proof:
From the sine rule we know sin(ACB)=AB/BC=3/5. The angles AMC and ACB are equal; therefore sin(AMC)=3/5 = MF/AF.
(V.) AF = 25/4
Proof:
As the triangle AMF is a right triangle, AF^2 = AM^2 + MF^2 AM^2 = 25 and MF = 3AF/5, which yields the desired result.
One can see from the diagram that
Area(AEDF) = Area(AEDM) - Area(AMF) = AM^2 - (AF MK/2) = 25 - (25 3)/8 = 125/8
yielding the desired result.
This question takes into account principles of similarity and trigonometry.
It is easy to see that the triangle is an Right angle triangle ABC (by the cosine identity, is you want it to be quite rigorous) is in fact a right angle triangle about A. Hence it can be inscribed inside a circle of diameter BC.
Then M would the centre of the circle, by the given information in the question and consequently AM = 5cm = MD =ED = AE = BM = MC = AM.
Now, for the trigonometric and similar part.
Tri(ABM) can now be see as an isosceles triangle. Hence, Angle(ABM) = Angle(BAM) = the larger acute angle of the 345 right angle triangle. therefore, Angle(MAF) = the smaller acute angle of the 345 right angle triangle. (because, Angle(BAM) + Angle(MAF) = 90 degrees. This consequently shows that Traingle(MAF) is similar to Triangle(BCA) (which already was similar to the 345 right angle triangle). therefore the in Triangle(MAF) MA = 5cm. and then one can work out its area (which would be (1/2) (15/4) (5) ).
All that remains is to calculate the area of the Square(AMDE) and subract from that area of the Triangle(AMF) which would give:
125/8
ABC triangle ko right angle hai find AM =5 and MF=25/4 abd AMF is right angle so Area 1/2 15/4 5==75/8 so total square ka area-(75/8) = 25-75/8=125/8
Log in to reply
If AM is the side of square and MF is part of the side of the same square, how can it be greater than side itself?
AM=MC=MB = 5, so area of AMED= 5 5=25, tg ACB=6/8= tg MAF =MF/AM, thus MF= 15/4 Area of AFDE = area AMDE-area of AMF =5 5-1/2 5 15/4= 125/8
AB = 6, BC=10, AC=8...if we check by using Pythagorean Theorem, --> c2=a2+b2, this signify that triangle is a Right Triangle...
so therefore; Sin Ѳ = 4/5, Cos Ѳ = 3/5, tan Ѳ = 4/3... Area of ABM = AB x BM x sin Ѳ/2 = 6 5/2 4/5 = 12
Using Cosine Law; AM^2=AB^2+BM^2-2 AB AM cosѲ AM^2=6^2+5^2-2 6 5 3/5 AM^2=25 AM = 5 therefore Triangle ABM is Isosceles Tri., so, angle BAM = ABM, equal to Ѳ, Angle MAF =90-Ѳ, then
for Triangle AMF, since this is a Square, so angle AMF = 90, Angle MAF =90-Ѳ, then Angle AFM = Ѳ, for MF = ? for similar triangle, MF /5 = 3/4, so MF = 15/4
Area of AFM = AM MF/2 = 5 15/4/2= 75/8 Area of AEDF = Area of AEDM - Area of AFM Area of AEDF = 5*5-75/8
Area of AEDF = 25 - 75/8 ===>>>125/8..Ans..
- Given: AB=6, AC=8 and BC=10. AM=MC=5 (Since, M is the midpoint of BC). Also, AMDE is a square.
- It can be observed that: BC² =AB² +AC² . This says that ABC is right angled at A.
- By using theorem "In a right angled triangle, the median from right angle to hypotenuse is half the length of hypotenuse", MC=MB=MA=5. Also, since AMDE is a square MA=AE=ED=DM=5. ( The angles of a square are all equal to 90°).
- Now, ∠BAM+∠MAC=90°; ∠MAC+∠CAE = 90°. Thus, ∠BAM = ∠CAE---(1).
- Since AE||MD with AC as a transversal, ∠MFA = ∠CAE (alternate interior angles)---(2).
- From (1) and (2), ∠BAM=∠MFA=∠CAE---(3).
- Triangle AMC being isosceles (AM=MC); ∠MAC=∠MCA. Also, triangle ABM is isosceles (MB=MA); ∠BAM=∠MBA ---(4).
- From (3) and (4), ∠BAM=∠MFA=∠CAE=∠MBA ---(5)
- Now, ∠MBA=∠MFA (from (5)); ∠BAC=∠AMF=90° and ∠MCA=∠MAF (from isosceles triangle AMC). By AAA theorem, triangles ABC and MAF are similar triangles. Thus, (AB/MF)=(AC/MA)=(BC/FA). Or, (6/MF)=(8/5)=(10/FA).
- This gives: MF = 15/4 and FA =25/4.
- Area of quadrilateral AEDF = Area of square AEDM - Area of triangle AMF = 5²-((1/2) 5 (15/4)) = 25-(75/8) = 125/8 or 15.625 square units.
first the triangle is right angled triangle and I draw m x orthogonal AC then XF =2.25 then the area of triangle AMF=75/8 then the area of figure AEDF =25-75/8=125/8
in triangle abc <bac=90 as 8^2+6^2=10^2,so cos <acb=8/10 and sin<acb=6/10,now consider ab along x and ac along y so considering a at(0,0) c=(0,8)and b=(6,0).now since m divides bc in 1:1 so m=(3,4)by mid point formula.so am =5.now in triangle acm <acm=<mac=<acb as equal side subtend equal angle.also side of square=5.so area of square =25.now for triangle amf tan<maf(=<mac)=mf/am=6/8.mf=6 5/8=15/4.so area of traingle afm=(1 5*15)/8.subtract this area from area of square 25-75/8=125/8 which is our answer.
The solution lies in the property of triangle and specifically the right angle tri....The main idea is to prove the tri ABC and AMF identical and than need to bring out the ration of sides.........AB, AM, MC, BM, AE, DE, MD are all equal i.e. = 5. Putting the property of ratio for the 2 right angle tri ABC and AMF we get ---> AC(height)/AB(base) = AM(height)/MF(base)...........Putting the value we get MF and than subtract the Area of Triangle AMF from the Are of Square AMDE..............We are with our solution..........
The triangle ABC is clearly right angled since it followed the ratio 3:4:5. AM is the median and the quadrilateral AMDE is a square, so the triangle AMF is right angled and the triangles AMF and CAB are similar. Therefore, CA/AM=AB/MF=BC/FA(=K) => AM=8K & MF=6K =>Area of triangle AMF = 24K K & Area of Square = 64K K =>After subtraction, area of the shaded region is 40K =>only option in the choices that can be obtained for the value of K is 125/8 :)
First. Let us deduce the relationship between different sides and angles of the triangles and quadrilaterals.
We have AM being the median of a right triangle, which by Thales theorem, means that, BC is the diamater of the Circumcircle and M is the mid-point of BC and hence AM = BM = CM = BC/2 = 5
Now since AEDM is a square, AE = ED = DM = AM = 5
Now let us see ∆ ABC. Since AngleBAC = 90˚, we can deduce that AngleABC = tan^-1 (3/5) ; AngleACB = tan^-1 (4/5)
Now see ∆ABM, since AM = BM, it is an isoceles triangle. So AngleABM = AngleBAM = tan^-1(3/5) Now since AngleBAC = 90˚ = AngleBAM + AngleCAM Therefore AngleCAM = tan^-1(4/5)
Similarly if you consider ∆AMC, you will find that AngleAFM = tan^-1(3/5)
Now compare ∆BAC and ∆AMF. By virtue of angles that we found out, we have ∆BAC ~ ∆AMF. Therefore: BC/AF = AC/AM = AB/MF 10/AF = 8/5 = 6/MF Therefore: AF= 25/4 ; MF = 15/4
NOW, Area(AEDF) = Area(AEDM) - Area(AMF) Area(AEDM) = 5 X 5 = 25 Area(AMF) = 1/2 X AM X MF = 1/2 X 15/4 X 5 = 75/8
Hence, AreaAEDF = 25 - 75/8 = 125/8
Using Apollonius Theorem, AM=5=MC. So, ar(AMDE)=25. Since AMC is isosceles, angles A and C are equal. tan A=3/4=MF/AM=MF/5. So, ar(AMF)=75/8 as M=90 deg and ar(triangle)=1/2 bh=1/2 AM*MF. So, ar(AFDE)=ar(AMDE)-ar(AMF)=25-75/8=125/8
6^2 + 8^2 = 10^2 (Pitagorasz) AM=BC /2 =10/2=5...................... 5/8 = MF/6 ……… MF = 30/8.............. 5/8 = AF/10 …….. AF = 50/8............... area of quadrilateral= area of square – area of small triangle.......... area of square=25 =200/8 ....... area of small triangle= 5 30/8 /2 =75/8 ......... area of quadrilateral=200/8 -75/8 = 125/8
Used coordinate geometry with AC and BC as axes.It was fun.
A(AFDE) = As(AMDE) - At(AMF);
|AB| = 6; |AC| = 8; |BC| = 10;
As(AMDE) = |AM|^2; At(AMF) = |AM||MF|/2;
Tr(ABC) is rectangle in A, angle(A) = 90°, because
|AB|^2 + |AC|^2 = |BC|^2, 6^2 + 8^2 = 10^2;
so M, midpoint of BC is the circumcenter of Tr(ABC),
|BC| = 2|AM| = 2r, r = |AM| = |BC|/2 = 5, is the radius of the circle;
Also with formula of medians:
|AM| = (√(2(|AC|^2 + |AB|^2) - |BC|^2))/2 =
√(2|BC|^2 - |BC|^2)/2;
|AM| = √(|BC|^2)/2 = |BC|/2 = 5;
As = 5^2 = 25;
angle(AMF) = 90°;
angle(MAB) = angle(MBA),
because |AM| = |BM|, Tr(AMB) is isosceles, and also Tr(AMC); so:
angle(CAM) = angle(BCA);
Tr(MAF) is rectangle and similar to Tr(ABC):
|MF|/|AM| = |AB|/|AC|;
|MF| = |AB||AM|/|AC| = 6 x 5/8 =15/4;
At(AMF) = |AM||MF|/2 = 5 x 15/(2 x 4) =75/8;
At(AFDE) = 25 - 75/8 = 125/8 cm^2;
Given BM=MC=5 cm (Since M is the Mid point). Using the Pythagorean triplet 6-8-10 (6^2 + 8^2 = 10^2) it can be seen that angle BAC is 90 degree. Now divide AB into 2 equal parts by drawing a "perpendicular" to AB from M. and apply Pythagoras Theorem. You will get AM=5 cm. The Area of the given Square is 5 5 ( Area of a square is side side). Now let angle BAM=x degree. Since AM= BM=5 cm. angle BAM=ABM (Isoscles triangle property.) Now angle BAC is 90 deg and BAM is x deg. Therefore angle MAC = (90-x) deg and AFM is x deg ( Sum of Angles in a triangle 180). We see that Triangle AMC is "Similar" to triangle ABC ( Similarity criterion Angle AFM = Angle ABC, Angle BAC=Angle AMD.). Using Similarity it can be found that MF is 30/8. Therefore the Area of the Triangle AFM is (1/2) (5) (30/8) = 75/8. The area of the Shaded region can be found out by subtracting The Area of Square by the Area of The Triangle AFM i.e., ( 5*5 - 75/8 = 125/8).... Hope you got it....
Good Problem....enjoyed solving it
excellent solution
First of all 6 , 8 , 1 0 → 6 2 + 8 2 = 1 0 2 Thus by the converse of Pytagoras theorem △ A B C is rectangle. Since A M is the median, and we know every triangle rectangle can be inscribed in the diameter of a circumference we can see the median of the right triangle equals half the diameter. Therefore A M = 2 1 B C = 5 . That means A M = B M and △ A B M is iscoseles. Let ∠ A B M = α → ∠ B A M = α → ∠ F A M = 9 0 − α → ∠ A F M = α . This means they are similar. M F A M = B A A C M F 5 = 6 8 . M F = 4 1 5 Area quadrilater {AEFD} = Area square {AEDM} - Area triangle {AMF} = 2 5 − 8 7 5 = 8 1 2 5