A Ruled Prism
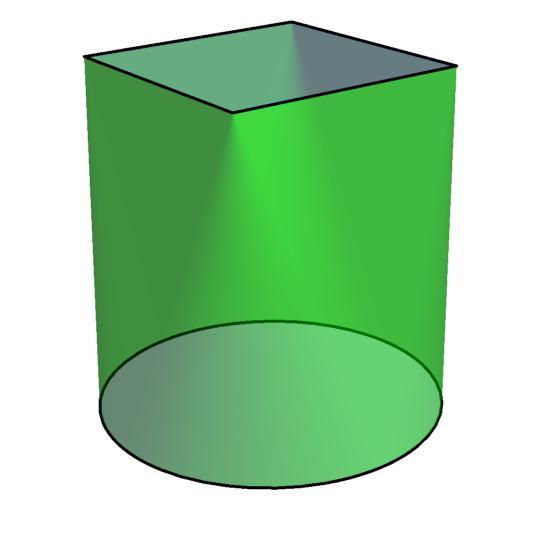
Define a ruled prism to be a solid with 2 parallel faces and a ruled surface joining the 2 parallel faces continuously and without overlap.
Given that you know the perpendicular distance between the 2 parallel faces and the areas of n cross-sections of the ruled prism, what is the minimum n such that you can know the exact volume of the ruled prism?
(You can choose which cross-sections to find the area of.)
The diagram above is an example of a ruled prism with a square and a circle as the parallel faces and a ruled surface connecting them.
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Imagine making a mat out of spaghetti pieces. Lay the pieces out in parallel. Tie the 'top' ends of all the spaghetti sequentially together loosely with a piece of thread. Similarly tie all the 'bottom' ends together. You've now made a mat. Joining the left and right hand sides together you can make a cylinder. However if you twist the top circle relative to the bottom circle you will get a hyperboloid, roughly a cylinder with a narrow waist, or hour glass shaped volume. Also consider the two end surfaces of the volume are identical very high aspect ratio rectngles but one rotated by 90 degrees from the other. If one knows the shape of the two end surfaces of the volume, height and one piece of spaghetti connecting them, then I think finding the volume is straightforward. I am sceptical whether two areas can encode this information.
Log in to reply
But the formalism of the ruled prism precisely encodes your idea of spaghetti strands. Each strand is one of the rules. Your hyperboloid will arise from choosing G j ( t ) = F j ( t − u ) for j = 1 , 2 . The parameter u is then the angle through which the top circle is rotated.
Log in to reply
True, upon rereading your answer I gather you take as known two cross-section shapes F and G, and their relative orientation. However on rereading the original question it seems you are asked for the number of cross-sectional areas (not shapes and orientations) required to define volume. I don't mean to criticise your answer in fact my understanding of the problem agrees with yours, which is quite satisfying.
Mark, are you saying that we can determine V from any two (perpendicular to the height so we don't have oblique sections) cross-sectional areas, or that only these two sections (h = 0 and h = (2/3) hmax) will work? It seems that if I flip the prism over onto the "other base", then I should get the same volume from two different sections (which correspond, in the original prism orientation, to h = hmax and h = (1/3)hmax.
So we have three options: a) only one pair of sections plus height defines volume (seems this is false by the prism flip example)
b) Any pair of sections plus the height (and plus the distance between the sections) defines the volume (is there one formula that can define this for all pairs of sections, or are there various formulae for various pairs of sections? E.g.Is there a formula for h=0 and h = (1/2)hmax?
c) Not every pair of sections plus height (and distance between) defines the volume, but there are many discrete pairs that can (just as the entire Cartesian plane does not satisfy a line equation, but an infinite number of specific x,y pairs do).
Which, if any, of a), b) or c) above can be proved?
I am usually much better at asking questions than at answering them, which is why I am a generalist rather than a specialist.
Getting really intuitive, hA0 and hAt would be the volumes of the two prisms you would get if each base was part of an "ordinary" prism (both bases identical) and A0 is area of the smaller base and At is the area of the larger (top) base. The volume of our ruled prism will be between these. So is the volume of the ruled prism just the average of these two? (hA0 + hAt)/2 = h[(A0+At)/2] = h*(average of the base areas).
This should work if it is true that for all ruled prisms, for any fraction of movement between h = 0 and h = hmax, you get the same fraction of movement between area = 0 and area = (At - A0) (where At>A0, and this is the positive difference between the base areas, or delta A).
Stated differently, if delta h is hmax - h0 = hmax, and delta A = At-A0 (At>A0, the positive base area difference), then for any perpendicular cross section at height Hi, If Hi/hmax = x, then Ai = A0 + x(delta A).
Simple example: if height of a cross section is 25% of the distance between 0 height and hmax, then Area of that section will be A0 plus 25% of the distance between A0 and At.
Does this violate our notion of area varying as square of length? I don't think so.
This particular instance is not the same as the similar polygon situation, where doubling the side of the polygon quadruples the area of the larger similar polygon. In our instance of the ruled prism, h is really quite decoupled from the areas: it is really more of a position indicator in an axis quite separate from area. So under that circumstance, we are asking if dA/dh is a constant or is some function of h.
For example, the volume of a cuboid (l w h) is a linear function of h, and dV/dh is (l*w), and the area of a triangle (bh/2) is a linear function of of h where dA/dh = b/2. It is only when the other dimensions are a function of height (such as similar polygons, or the sphere where the radius defines distance in all three dimensions) that square and inverse square rules (and similar cube rules) come into play.
So in our case it seems reasonable that the change in Area could be proportional to the change in height.
So is this rule true for ruled prisms (If Hi/hmax = x, then Ai = A0 + x(delta A)? And if it is, does that make this rule true (V = (hA0 + hAt)/2)?
Log in to reply
The formula V = h [ μ A ( h 1 ) + ( 1 − μ ) A ( h 2 ) ] holds provided that μ h 1 + ( 1 − μ ) h 2 μ h 1 2 + ( 1 − μ ) h 2 2 = 2 1 h = 3 1 h 2 and these equations are soluble for μ provided that 6 h 1 h 2 = 3 ( h 1 + h 2 ) h − 2 h 2 My solution was h 1 = 0 , h 2 = 3 2 h , μ = 4 1 , while Arjen provided h 1 = 3 1 h , h 2 = − 3 1 h , μ = 2 1 . There are clearly others.
I know that exterior derivative commutes with pullback and in this case it is clear that d(...)=dx^dy, but how can u express in (some, not necessarily basis) coordinates d (F(t) dt) if F is only a function of t? dF^dt? Can we arbitrary introduce an arbitrary one (say (dF/dj) dj^dt ) just because we know dt is not a top form?
The area of a parallel cross-section varies as a quadratic function of the parallel coordinate. Three cross-sections are sufficient to determine the precise function, and therefore the area.
However, we can optimize by choosing the cross-sections in a clever way. Let h be half of the height of the prism.
Note that if A ( z ) = a z 2 + b z + c with − h ≤ z ≤ h then V = ∫ − h h A ( z ) d z = ( 3 1 a h 2 + c ) ⋅ 2 h = : ⟨ A ⟩ ⋅ 2 h . Write the term in brackets as a linear combination of p A ( z 1 ) + q A ( z 2 ) for some z 1 , z 2 . Equating coefficients of a , b , and c separately, we find 3 1 a h 2 + c = p ( a z 1 2 + b z 1 + c ) + q ( a z 2 2 + b z 2 + c ) ⟹ ⎩ ⎪ ⎨ ⎪ ⎧ h 2 = 3 p z 1 2 + 3 q z 2 2 0 = p z 1 + q z 2 1 = p + q These are three equations with four unknowns, which therefore have some degrees of freedom. Use this freedom by choosing p = q = 2 1 so that z 1 = − z 2 . Then h 2 = 3 z 2 2 which implies z 1 , z 2 = ± 3 h .
In summary, if we calculate the average ⟨ A ⟩ = 2 1 A ( − 3 h ) + 2 1 A ( 3 h ) then the volume is ⟨ A ⟩ ⋅ 2 h . Knowing two areas of parallel cross-sections is therefore enough.
I dont think we need to add complex formulas to show that we need only two measurements. Basically, if we can take take two measurements and difference of height within those two measurements. Then we can find gradient of area per unit of height. So if we get gradients of area we can simply find volume by using integral for any height.
The gradient you are talking about isn't constant throughout the ruled prism. Besides, proving that the area varies quadratically with height requires much more than just intuition
Log in to reply
I disagree. Using MATLAB, we have corroborated the intuitive perspective of myriad ruled prisms.
Log in to reply
Disagree to what, I posit 2 claims here. What kind of ruled prisms did you use in MATLAB, because there are certainly ruled prisms whose cross-sectional area varies linearly with height (Like a cone). Besides, given your assumption that the gradient is constant, we don't need 2 cross-sections, we only need 1.
Log in to reply
@Julian Poon – The question asks for the minimum. We need the top and bottom cross section to know the two areas that require interpolation at each dz. The minimum occurs when dA/dz is a constant. For cross sectional areas A0 to A1 and height h, constant dA/dz = (A1 - A0) / h = ∆A/h . A(z) is then A0 + (∆A/h) × z . Integrating again over A(z) with respect to z gives the volume. A0 × z + ½(∆A/h) * z² on z from 0 to h gives V = A0×h + (A1 - A0) × h / 2 which simplifies to ½×(A0 + A1)×h. This is intuitively the average of the volume for two prisms with cross sectional areas A0 and A1 of equal heights, h.
We need at least two cross sections to determine the overall ∆A/∆z (giving us a constant ≥ 0, if zero we could have hypothetically gotten away with only one section but we needed to measure two before making that determination). More than 2 cross sections would be needed iff dA/dz was not constant. Since we need at least 2 , then 2 must be the minimum that can be used to calculate the volume.
Log in to reply
@Jacob Lubecki – I am very well aware that the minimum number of cross sections is 2 (I'm the author of this problem). I was responding to this solution's poster on his assumption that the area of the cross section varies linearly with height, which isn't true. Should the area of cross section vary linearly with height, we would only need the area of the middle cross section.
Suppose the area of cross section at height h is equal to a 0 + a 1 h , as followed by the linear assumption, then
A = ∫ 0 H a 0 + a 1 h d h = H ( a 0 + 2 1 a 1 H ) = H a 1 / 2
Where H is the height of the ruled prism and a 1 / 2 is the area of cross section at h = 2 1 H . Hence should the cross section vary linearly with height, we would only need 1 cross section.
However, by stokes theorem the cross sectional area varies quadratically with height, and as shown in Arjen's solution, we would need 2 cross sections
Is the area varying quadratically with height even relevant? Imagine a prism with circles of radius r and 2r as the top and bottom. When height = 0 we have the r, when height = hmax we have 2r. It seems intuitive that when height = 1.5 hmax the radius is 1.5 r and so forth for any value of height (and if we had r and 3r 1.5 hmax would be radius of 2, etc.) So intuitively we only need to know area at h = 0 and area at h = hmax to be able to infer area at any value of h. So one comes up with 2 cross sections without caring how one computes any actual area.
Log in to reply
I'm not talking about a specific case of a ruled prism here. You would need to prove that you can use 2 cross sections to find the volume of any ruled prism, hence you will need a description that can be generalised to any ruled prism. In general, the area varies quadratically with height and this property is then used to prove that 2 cross sections are necessary.
For your special case, it just so happens that the cross-sectional area varies linearly with height, and for such special cases, only 1 cross section is required (when h = 2 1 h m a x ).
The image I used in the problem as an example of a ruled prism (with a square and circle face) is an example where the cross-sectional area varies quadratically with height in general, and whose volume differs depending on how I define the ruled surface between the 2 faces. See here for further illustration.
Log in to reply
@Julian Poon – If in general area varies quadratically with height, I don't see how it is possible to create a special case where it only varies linearly with height.
In ruled prism environment I don't think that area varies quadratically with height. It doesn't even vary linearly with height, it seems. Let's expand my special case a bit to a "similar prism" where both bases are similar polygons.
Let's take squares of side s and side 2s. I can separate those two squares by h, by 2h, by 10h by 1,000h ... you get the idea. The s^2 and 4s^2 areas remain the same regardless of the h I chose to separate them by. So Area is completely independent of h in this setting (not quadratic and not even linear).
Now Area varies quadratically with height in the case where h0 corresponds to A0 = 0 (the bottom base of the similar prism is a point), where what I have is an inverted pyramid, and the radii or sides of sections at different Hi turn out to be sides of similar triangles. But our generic similar prism is a truncation of such a pyramid, and h = 0 is not the point of a pyramid but is this truncation of it where A0 is not 0. So the values of h are arbitrary, and what matters is the change in h. Not unlike dealing with Kelvin and Celsius temperature scales: values are very different but intervals are the same.
I can make the same case for two non-similar polygons as the bases of a general ruled prism.
What does vary with change in h is the difference between Ai and A0 (Ai is the area at Hi and A0 is the area at h = 0).
(Ai - A0) = (h/hmax)(At - A0) where At is the Area at hmax (the top) and At>A0. So when the height is some fraction between 0 and h max, the area is the same fraction between A0 and At.
So with two areas, we can establish dA/dh, which I think is constant regardless of position on the h axis, and knowing that and hmax, and the position on the h axis of the two known areas, it should be possible to compute A0 and At and any Ai. Integrating all Ai should be the volume.
Or maybe dA/dh is constant only for similar prisms? If the this rule has this limitation, then having dissimilar bases makes dA/dh unpredictable (or is it predictable in a more complicated way?), which if true would seem to make knowing volume from just two sections in all cases impossible.
Finally, for similar prisms (my circle and square cases), is one section at h = (1/2) max sufficient? The value of h isn't the issue, it is how interval change in h results in interval change in A. How do I learn dA/dh from a single section?
Or does symmetry come to the rescue? Does knowing that dA/dh is constant, and that I have as much h to travel in either direction from the midpoint solve the problem, regardless of the value of dA/dh?
Or in other words, is it true that "for any circle or polygon, all possible similar prisms of identical height that contain that circle or polygon as their midpoint cross section will have the same volume"? And is that volume A(at h = 1/2)*h?
I think yes for the similar prism case. If dA/dh is constant for any ruled prism, then then wouldn't knowing the midpoint section area and h also be enough for them? And if dA/dh is not constant, then how is two enough in all cases?
It took me 5 seconds to type 2. Using MATLAB, we can corroborate the intuitive perspective of myriad ruled prisms, if you are a stickler for solving in a non-intuitive way.
Log in to reply
It takes 1 second to make an intelligent guess 2. However, if you want to prove rigorously for all possible ruled prism then you'll have to get your hands dirty
Suppose that the edge of the bottom face of the ruled prism is described by the function F ( t ) = ( F 1 ( t ) , F 2 ( t ) , 0 ) 0 ≤ t ≤ 1 and that the edge of the top face of the ruled prism is described by the function G ( t ) = ( G 1 ( t ) , G 2 ( t ) , h ) 0 ≤ t ≤ 1 where, moreover, the point with coordinates F ( t ) is joined by a rule to the point G ( t ) for each 0 ≤ t ≤ 1 . Here h is the height of the ruled prism.
The cross-section of the surface at height z , where 0 ≤ z ≤ h , is defined by the function ( X z ( t ) , Y z ( t ) , z ) = h h − z F ( t ) + h z G ( t ) for 0 ≤ t ≤ 1 . The area of this cross-section is given by Stokes' Theorem as A ( z ) = = = 2 1 ∫ 0 1 [ X z ( t ) Y ˙ z ( t ) − Y z ( t ) X ˙ z ( t ) ] d t 2 1 ( h h − z ) 2 ∫ 0 1 [ F 1 ( t ) F ˙ 2 ( t ) − F 2 ( t ) F ˙ 1 ( t ) ] d t + 2 1 ( h z ) 2 ∫ 0 1 [ G 1 ( t ) G ˙ 2 ( t ) − G 2 ( t ) G ˙ 1 ( t ) ] d t + 2 h 2 z ( h − z ) ∫ 0 1 { F 1 ( t ) G ˙ 2 ( t ) + G 1 ( t ) F ˙ 2 ( t ) − F 2 ( t ) G ˙ 1 ( t ) − G 2 ( t ) F ˙ 1 ( t ) } d t α + β z + γ z 2 for some constants α , β , γ . The volume of the prism is then V = ∫ 0 h A ( z ) d z = α h + 2 1 β h 2 + 3 1 γ h 3 and it is easy to see that V = 4 1 h [ A ( 0 ) + 3 A ( 3 2 h ) ] so we need just 2 cross-section areas (plus the height of the prism) to determine V , namely the area of the base and the area two-thirds of the way to the top.