A simple integral?
Evaluate the following integral
∫ cos 3 ( x ) sin ( x ) d x
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Eyyy, how you doing. It's been quite a while :)
The main reason I made this question is because of the two ways you could integrate this. What the question is actually asking for in simplest terms is
∫ sec 2 ( x ) tan ( x ) d x
If you u-sub u = tan ( x ) or u = sec 2 ( x ) you get the two different results.
Log in to reply
Hey Trevor. Bet you're glad to be done with the school year. Spending much time on the golf course? Things seem a little slow here on Brilliant; I guess a summertime slowdown is to be expected, but it seems a little more pronounced this year compared to last.
I had figured that your objective in posting this question was to highlight the importance of the general constant and its amorphousness, (hey, that's actually a word :) ), and thus took as direct an approach as possible to evaluate the integral. I hadn't thought of the u-sub with u = sec 2 ( x ) before, but it does do the job, as well as sets up the two (supposedly) different results scenario.
Log in to reply
Yes, I've been super busy with golf. Having math withdrawals. And yes couldn't be happier to be done with school. I'm also thinking the slow down is due a lot to all the JEE participants who no longer need to practice as much.
Also correct, I posted this question to show the importance of C. Im trying to learn all of AP calc before the school year starts (I'll be in pre-calc honors next year) so I can take the exam and get a 5 in order to take Multivariable Calc, Number theory, and non-Euclidean geometry my senior year. That's another reason I haven't been on Brilliant as much, I'm learning from a text book. Starting next week however, I will have more than enough free time to spend doing math on Brilliant and from the text book.
Log in to reply
@Trevor Arashiro – Ambitious. :) There wasn't even the option of covering those topics when I was in grade 12. Is the plan to get college credit for those topics, or are you just eager to cover them, (and in the process get a leg up for when you get to college)?
Log in to reply
@Brian Charlesworth – Those courses usually have between 1-3 students per year so not many people take them. I'm taking them partially for fun, partially because I'm bored with the math I'm in now., and partially because they look good on my résumé for college.
Log in to reply
@Trevor Arashiro – Makes sense. Great student/teacher ratio. :)
may be not but good ideas
Then There should be different notations for C in both terms, right....
∫ c o s 3 ( x ) s i n ( x ) d x ∫ ( c o s ( x ) s i n ( x ) ) ( c o s 2 ( x ) 1 ) d x ∫ t a n ( x ) s e c 2 ( x ) d x Now, use U-substitution, but notice that two substitutions can be made u = t a n ( x ) d u = s e c 2 ( x ) d x Or u = s e c ( x ) d u = s e c ( x ) t a n ( x ) d x Either substitution will yield: ∫ u d u ∫ u d u = 2 1 u 2 + c Depending on what substitution you made, the answer will either be: 2 1 t a n 2 ( x ) + c Or 2 1 s e c 2 ( x ) + c
∫ cos 3 x sin x d x = ∫ tan x sec 2 x d x
Take t = tan x ⇒ d t = sec 2 x d x
∫ t d t = 2 t 2 + c = 2 tan 2 x + c = 2 sec 2 x + c − 2 1 = 2 sec 2 x + C
The actual difference here is the constant of integration, but hence we do not know what it is we can simply assume it to be some c
Moderator note:
Yes, here's a slightly condensed version of your solution.
= ∫ cos 3 ( x ) sin ( x ) d x = ∫ tan ( x ) d ( tan ( x ) ) 2 1 tan 2 ( x ) + C = 2 1 ( sec 2 ( x ) − 1 ) + C = 2 1 sec 2 ( x ) + C ′
use substitution : cos x = u ↔ − sin x d x = d u
do the integral and you will get: 2 sec 2 ( x ) + c
wait a second... remember trigonometric identity: sec 2 ( x ) = tan 2 ( x ) + 1
thus 2nd choice is also right.
that's why it's very important to reflect on your answer before submitting.
It is not the rightway
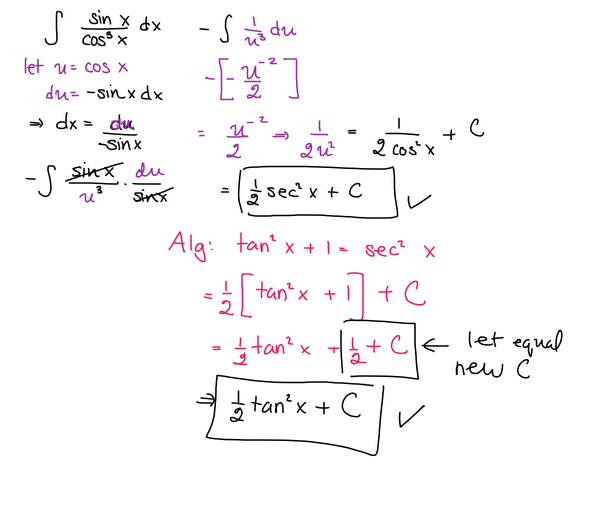
Using the substitution u = cos ( x ) , we have that d u = − sin ( x ) d x . The integral then becomes
∫ − u 3 1 d u = 2 u 2 1 + c = 2 sec 2 ( x ) + c .
This can also be written as 2 tan 2 ( x ) + 1 + c = 2 tan 2 ( x ) + c , where the "extra" 2 1 term was absorbed by the general constant c . Thus both the explicit options provided are correct, since they differ only by a constant.