A Number Line Problem
You pick two numbers
at random
between 0 and 10 inclusive, what is the probability that 5 lies between these two numbers?
Hint: note the difference between the terms 'numbers' and 'integers'.
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Marvellous solution! Everyone loves a graphical representation :)
Rehamn Amjad, Here is a new problem for you ... Can you apply Graphical representation to solve this ?
You pick two numbers at random between 0 and 10 inclusive, what is the probability that a prime number lies between these two numbers
Log in to reply
It's the same diagram but with the two red squares covering the 0-2 and 7-10 ranges.
Log in to reply
What if you pick numbers 3 and 5, the number between them is NOT prime.
The graphical representation for picking two numbers with at least one prime number in between them would like this:
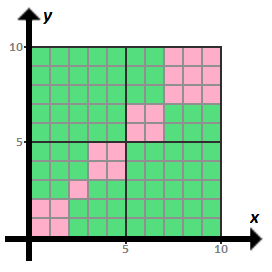
Since 7 8 out of 1 0 0 squares are green, there is a 1 0 0 7 8 = 5 0 3 9 = 0 . 7 8 probability that a prime number lies between the two numbers.
Log in to reply
I'm glad my graph matches yours. I must ask, how do you manage to make it look so much better?
Thank you for the extension. My diagram may look a bit messy but it's
1
0
0
7
8
=
0
.
7
8
.
I drew in a line of symmetry since one can quickly notice that it doesn't matter which way around the numbers are. It is interesting to note that the squares containing the red sections have 2 prime numbers on their vertices. As this is a region where you have the randomly selected numbers lying between 2 primes.
Log in to reply
That is an interesting observation. It means if you were to extend the problem from selecting two numbers in ( 0 , 1 0 ) to two numbers in ( 0 , n ) , the probability of finding a prime between them is related to the average size of the square of the prime gaps below n .
Awesome application of the principal Rehman and David.!
∫ 0 1 0 ( ∫ 0 1 0 1 d m ) d n ∫ 0 1 0 ( ∫ 0 1 0 Boole [ n ≤ 5 ≤ m ∨ m ≤ 5 ≤ n ] d m ) d n ⇒ 2 1
Boole is a function whose inputs are logical (true or false) values and which returns 0 for false and 1 for true.
There are 2 ways I would approach this problem.
1. The first random number you pick (call this A ) WILL NOT affect this probability. This is because on a continuous number line, A is definitely above or below 5 (as the probability of getting 5 itself is infinitely small).The second number you pick (call this B ) WILL affect the probability. For 5 to lie between A and B , you want a B on the other side of 5 to A , ie, if B lies to the right of 5 then A must lie to the left and vice versa. The probability of this is happening is 1 0 5 which equals 0.5.
2. Consider the probability of some random number A being less than 5 is 1 0 5 and some random number B being greater than 5 is 1 0 5 . Thus, in this case of A ≤ B , the overall probability is 1 0 0 2 5 (as the 2 probabilities are multiplied). Likewise, in the case of B ≥ A , the overall probability is 1 0 0 2 5 . These probabilities sum to 1 0 0 5 0 which equals 0.5.
Note that A and B are examples of continuous random variables . The probability of a single number such as 2.73 or 6 being chosen is infinitely small. Instead, we consider the probability of a random number lying in a range.
The total number of ways in which we can select 2 numbers such that 5 lies in between them is 25.And the total number of ways in which we can select any two numbers from the given 11 numbers is 55.Therefore is not the required probablity 25/55 ?
Log in to reply
Apologies, I should make the distinction between numbers and integers here. Since the probability of picking 0, 1, 2, 3, ... 10 is infinitely small (as you may end up with a number between 2 and 3, eg, 2.427394941 even though the probability of this number being picked is also infinitely small), you must consider ranges instead. The range here is 10 (since 10 - 0 = 10). Using this, we can say the probability of having a number between 0 and 1 would be 1/10. Likewise, the probability of picking a number between 2 and 5 would be 3/10.
yeah even i got 25/55
Log in to reply
See my reply to other comment, hopefully that clears things up :)
If the first number is an x -coordinate and the second number is a y -coordinate, then the following square represents all the possible ways to pick the two numbers, where the green regions represent coordinates that have a 5 between them and the red regions represent coordinates that do not:
Since half the diagram is shaded green, the probability is 2 1 = 0 . 5 .