A Simple Sangaku
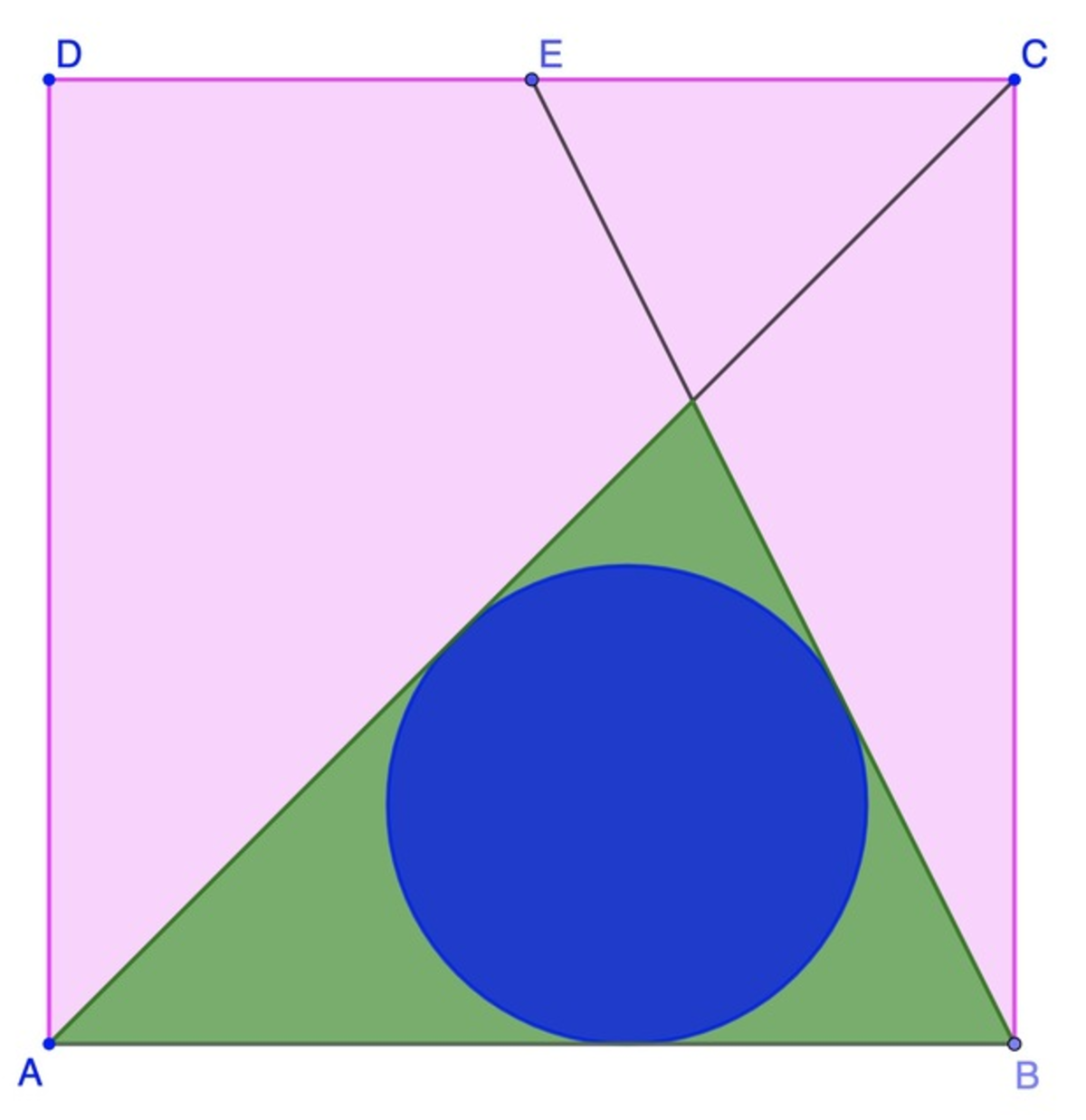
A B C D is a unit square. E is the midpoint of D C . What is the radius of the inscribed circle?
If the answer can be expressed as d 1 + a + b − c , provide a + b + c + d as the answer.
The answer is 23.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Great solution, I had a similar approach. But isn't there a negative sign in front of 1 0
Log in to reply
Sorry, fixed. Thanks
Log in to reply
@Pi Han Goh
Sir please can you help me in this problem
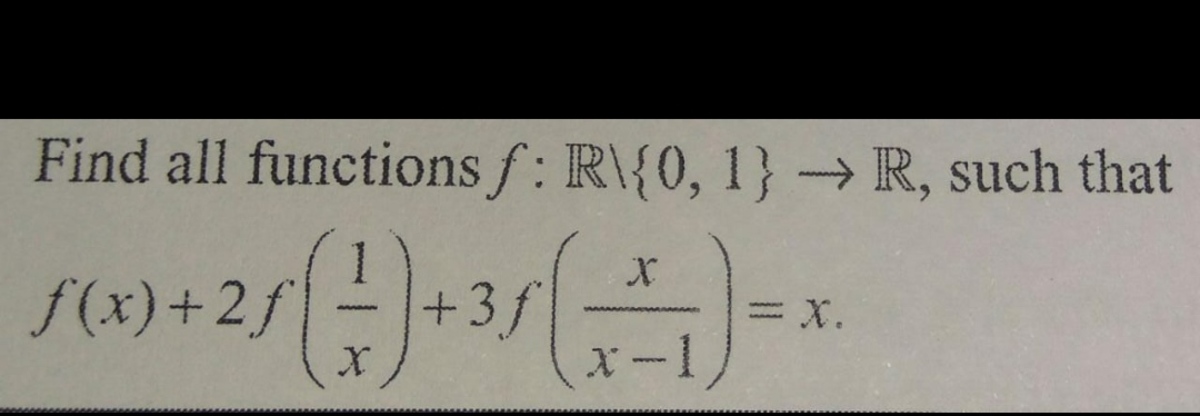
Thanks in advance
Log in to reply
@A Former Brilliant Member – What have you tried? Last time we interacted, I've suggested that you show me where you're stuck, but you didn't give me a response after that.
Log in to reply
@Pi Han Goh
–
@Pi Han Goh
Sorry, for not giving response. Because I understood what you wanted to say. You want to say that I should ask good questions of mathematics only and also show the work which i have done behind that question. Correct? I agree with you. In the above question. I am recently started solving this types of question and I have read the theory also.In this types of question first I didn't able to solve and then when I see the solution, I understood it whole That's the problem with me . For the last time give the solution of this question, Please .from next time will I will definitely show my work.
Thanks in advance
Log in to reply
@A Former Brilliant Member – Hint: You can interpret this equation with 3 variables on the left-hand side of the equation. If you replace x with x 1 or with x − 1 x , you will form another 2 equations.
Hint 2: Solve a system of linear equations.
Log in to reply
@Pi Han Goh
–
@Pi Han Goh Sir,
Original equation
f
(
x
)
+
2
f
(
x
1
)
+
3
f
(
x
−
1
x
)
=
x
When I replace
x
with
x
1
f
(
x
1
)
+
2
f
(
x
)
+
3
f
(
1
−
x
1
)
=
x
1
When I replace
x
with
1
−
x
x
f
(
x
−
1
x
)
+
2
f
(
x
x
−
1
)
+
3
f
(
x
)
=
1
−
x
x
Now, I am stucked in solving this
3
equations?
Log in to reply
@A Former Brilliant Member – You didn't adjust the right-hand side of the equation.
Assuming you have revised these equations, you may see that you (almost) got a system of equations:
a + 2 b + 3 c = x b + 2 a + ? = x 1 ⋯
Solve by elimination...
Log in to reply
@Pi Han Goh – @Pi Han Goh Now it's corrected. at you question mark in your latest comment, it is f ( 1 − x 1 ) should I assume it as d . After that there are 4 equations which would be difficult?
Log in to reply
@A Former Brilliant Member – Yes, I didn't say that you will only have to form 3 equations with 3 variables (in the left-hand side). Great creative with different substitutions and you can construct a sufficient number of systems of linear equations to be solved.
Log in to reply
@Pi Han Goh – @Pi Han Goh Give me Hint.
Log in to reply
@A Former Brilliant Member – Okay I have to admit I don't have a cleanest nor rigorous approach here, but here goes:
Try substituting x = − 1 , 2 1 , 2 into the equation, solving these equations you will get f ( − 1 ) = 2 4 − 1 1 , f ( 2 1 ) = 2 4 3 , f ( 2 ) = 2 4 2 1 .
Now try substituting other reasonably small rational numbers and see if you can solve the other new system of equations.
At the end of the day, you will know plenty of values of f ( p ) = q , where p and q are already known.
Then try to figure out if it's a polynomial function, logarithmic function, rational function, exponential function, etc.
My method here isn't completely rigorous because I don't think I know how to prove the existence of all solutions (or any solution).
You should try posting this question here to get a more comprehensive answer. My knowledge of functional equations isn't great...
Log in to reply
@Pi Han Goh – I'm not doubting the quality of this question, but did your question come from a reliable source? If it's a math Olympiad book or a renowned functional equation textbook, then I'm afraid that this is beyond my capabilities...
Log in to reply
@Pi Han Goh – @Pi Han Goh No. In India a exam is there name (IITJEE) . Function is a subtopic in this exam. This type of question generally asked in that exam. For more information you can search in the web also.
Log in to reply
@A Former Brilliant Member – Ah so it must be a quality question. Unfortunately, I do not know how to solve this rigorously. Sorry.
But I'll definitely keep you posted if I found any new insight...
@Pi Han Goh
Sir can you please help me in this integration
∫
0
2
π
1
+
α
cos
2
θ
d
θ
α
is constant
Thanks in advance
Log in to reply
Read up Elliptic integrals.
You should try posting your questions in the note , that will garner more attention quickly.
@Pi Han Goh , Have you seen the Matrix Series, because your status is "follow the white rabbit" ??I'm a fan!!
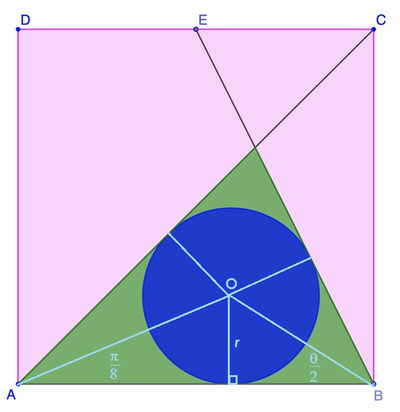
Let the center of the circle be O . Then O is also the incenter of the green triangle. Therefore, O A bisects ∠ C A B ⟹ ∠ O A B = 8 π and O B bisects ∠ E B A = θ ⟹ ∠ O B A = 2 θ . Let the radius of the circle be r . Then
tan 8 π r + tan 2 θ r 2 − 1 r + 5 − 1 2 r = 1 = 1 Since 1 − tan 2 8 π 2 tan 8 π = tan 4 π = 1 and 1 − tan 2 2 θ 2 tan 2 θ = tan θ = 2
⟹ r = 2 − 1 1 + 5 − 1 2 1 = 2 + 1 + 2 5 + 1 1 = 2 2 + 5 + 3 2 = 8 + 5 + 4 1 0 − 9 2 ( 2 2 + 5 − 3 ) = 2 + 2 1 0 2 2 + 5 − 3 = 2 ( 1 0 + 1 ) ( 1 0 − 1 ) ( 2 2 + 5 − 3 ) ( 1 0 − 1 ) = 2 ( 9 ) 4 5 + 5 2 − 3 1 0 − 2 2 − 5 + 3 = 2 ( 9 ) 3 5 + 3 2 − 3 1 0 + 3 = 6 1 + 5 + 2 − 1 0
Therefore, a + b + c + d = 5 + 2 + 1 0 + 6 = 2 3 .
Splendid approach!
looks like you got to practice some radical arithmetic, huh? :) nice presentation.
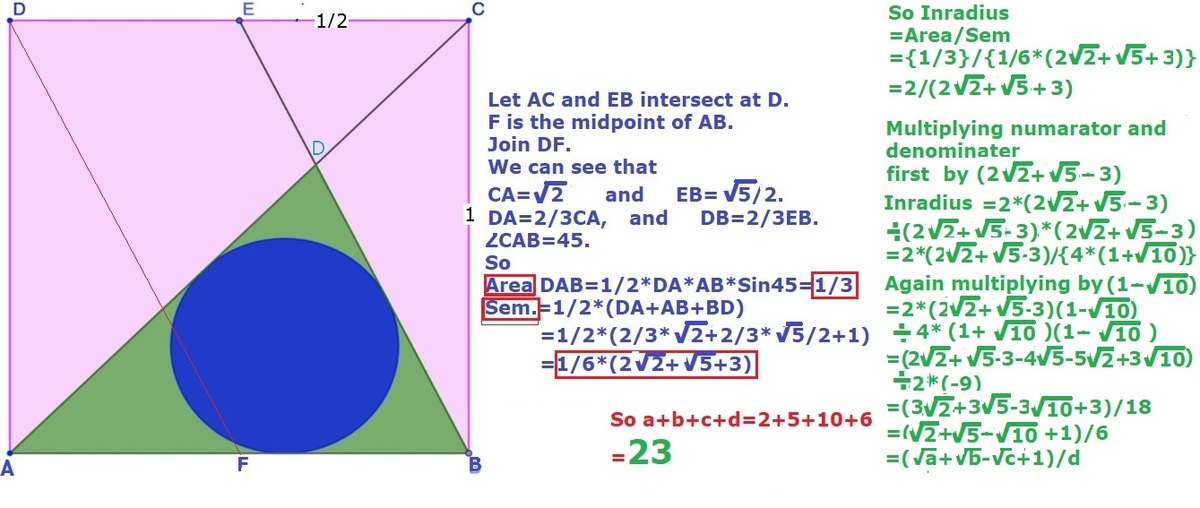

Plot this on the Cartesian plane with A ( 0 , 0 ) , B ( 1 , 0 ) , C ( 1 , 1 ) , D ( 0 , 1 ) , E ( 1 / 2 , 1 ) .
The equation of the straight line E C is x − 1 / 2 y − 1 = 1 / 2 − 1 1 − 0 . And the equation of the striaght line A C is y = x .
Solving these two equations simultaneously gives the intersection point F ( 2 / 3 , 2 / 3 ) .
So we have all the 3 coordinates of the triangles, by Pythagoras theorem, the lengths of this triangle is 1 , 3 5 , 3 2 2 .
Using the formula for the area of a triangle, A = r s , where r is the radius of the inscribed circle and s is the semiperimeter of the triangles gives r = 6 1 + 2 + 5 − 1 0 .
The answer is 2 + 5 + 1 0 + 6 = 2 3 .