A Singular Triangle

The figure shows a triangle A B C and its incircle. △ A B C has integer side lengths. If C F = F B and A G = G H = H F , what is its smallest possible perimeter of △ A B C ? The figure is not drawn to scale.
The answer is 28.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
@David Vreken What symmetry are you using to justify A P = F Q ?
Log in to reply
I rearranged the order of my solution to try and clarify things.
I would like to propose my solution to understand what is wrong with it
Let AG = GH = HF = x Let CP = CQ = y
AP = AR = sqrt(2).x FQ = sqrt(2).x
AC = AP + CP = sqrt(2).x + y
CF = CQ + FQ = sqrt(2).x + y
BC = 2.sqrt(2).x + 2.y
Since CF = FB, BQ = FB + FQ = sqrt(2).x + y + sqrt(2).x
Since BR = BQ, BR = 2.sqrt(2).x + y
AB = AR + BR = sqrt(2).x + 2.sqrt(2).x + y = 3.sqrt(2).x + y
Since each of AC, BC, AB are integers, their differences must also be integers
BC - AC = sqrt(2).x + y, say = p AB - AC = 2.sqrt(2).x, say = m AB - BC = sqrt(2).x - y, say = q
2.sqrt(2).x = m so x = m/2.sqrt(2).
p = sqrt(2).x + y = m/2 + y
q = sqrt(2).x - y = m/2 - y
So, p + q = m
If m = 1, that means, either p is 0 or q is 0. Since q < p, so q is 0 and p is 1.
Since p = m/2 + y, and m = 1, p = 1, so y = 1/2
So, x = 1/2.sqrt(2) Do note the picture says that the diagram is not drawn to scale, so I suppose, it is possible for x < y.
So, AC = sqrt (2)/2.sqrt(2) + 1/2 = 1 AB = 3.sqrt(2)/2.sqrt(2) + 1/2 = 2 BC = 2.sqrt(2)/2.sqrt(2) + 2.1/2 = 2
So, minimum perimeter, comes to 5.
Log in to reply
You also need to consider the restraint that C , F , and B are in a straight line. The sides you found for △ A C F are 1 , 1 , and 2 2 3 , and by the law of cosines ∠ A F C ≈ 5 7 . 9 7 ° , and the sides you found for △ A B F are 1 , 2 , and 2 2 3 , and by the law of cosines ∠ A F B ≈ 1 5 2 . 1 1 ° , so in your solution ∠ A F C + ∠ A F B = 1 8 0 ° .
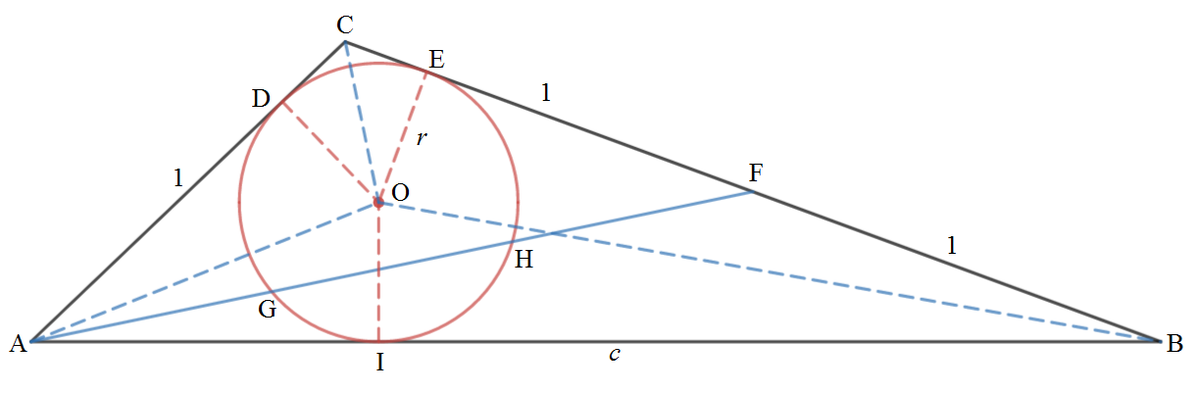
Because of symmetry, △ C A F is isosceles with C A = C F . Let C A = C F = 1 , this means that C B = 2 . Add in the inradii of length r O D , O E , and O I . Then we have:
⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ C A : C B : A B : r cot 2 A + r cot 2 C = 1 r cot 2 B + r cot 2 C = 2 r cot 2 A + r cot 2 B = c
C A + C B − A B : 2 r cot 2 C = 3 − c ⟹ c = 3 − 2 r cot 2 C .
We note that A G = G H = H F = 3 2 sin 2 C . By tangent-secant theorem of circles we have A D 2 = A G ⋅ A H = 3 8 sin 2 2 C , ⟹ A D = 3 2 2 sin 2 C . We also note that A D + D C = 3 2 2 sin 2 C + r cot 2 C = 1 , ⟹ r cot 2 C = 1 − 3 2 2 sin 2 C and c = 1 + 3 4 2 sin 2 C .
By cosine rule ,
c 2 ( 1 + 3 4 2 sin 2 C ) 2 1 + 3 8 2 sin 2 C + 9 3 2 sin 2 2 C 3 8 2 sin 2 C ⟹ 3 4 2 sin 2 C ⟹ c = 1 2 + 2 2 − 2 ( 1 ) ( 2 ) cos C = 5 − 4 ( 1 − 2 sin 2 2 C ) = 1 + 8 sin 2 2 C = 9 4 0 sin 2 2 C = 3 8 2 × 4 0 9 × 3 4 2 = 5 8 = 1 + 5 8 = 5 1 3 For sin 2 C = 0
Therefore a : b : c = 2 : 1 : 5 1 3 and the smallest integer side lengths triangle is 1 0 : 5 : 1 3 with a perimeter of 2 8 .
Clear and clean. Thank you!
Log in to reply
Thanks for the nice problem too. I told me some time but it was interesting.
Log in to reply
I was beginning to think I had finally stumped you. :)
Log in to reply
@Fletcher Mattox – Yes, almost... but I didn't want to disappoint you or I wanted to disappoint you.
Hints: Consider the power of A and F to the incircle in different ways in terms of AB,BC,CA, then the you'll find the ratio.
Solution will be posted soon
Those interested in the solution may please check this out: file:///C:/Users/Admin/Downloads/atria solve a geometry problem.pdf
@ajit athle , your file will have to be uploaded to the Brilliant web site before anyone (other than you) can see it. To do this, click on the "add image" icon.
Where do I find "add image"?
Log in to reply
Under "Add your own explanation" is a row of buttons starting with L a T e X . Click the third button from the left.
Add C D perpendicular to A F and label the points of tangency P , Q , and R , as shown below:
Let x = A G = G H = H F , y = F Q , and z = C F = F B .
By the tangent-secant theorem , F Q 2 = H F ⋅ G F = A G ⋅ G F = A P 2 , so A P = F Q = y and y 2 = x ⋅ 2 x = 2 x 2 .
Also, since the segments from a point to two tangent points on the same circle are equal, C P = C Q , which means C A = C P + A P = C Q + F Q = C F = z , and A R = A P = y and R B = Q B = F Q + F B = y + z , which makes A B = A R + R B = 2 y + z .
△ C D F ≅ △ C D A by HL congruence, so D F = 2 1 A F = 2 1 ( A G + G H + H F ) = 2 3 x .
From △ C F D , cos ∠ C F D = C F D F = 2 z 3 x , which means cos ∠ A F B = cos ( 1 8 0 ° − ∠ C F D ) = − cos ∠ C F D = − 2 z 3 x .
By the law of cosines on △ A F B , cos ∠ A F B = 2 ⋅ F B ⋅ A F F B 2 + A F 2 − A B 2 , or − 2 z 3 x = 2 ⋅ z ⋅ 3 x z 2 + ( 3 x ) 2 − ( 2 y + z ) 2 , which after substituting y 2 = 2 x 2 from above solves to y = 5 4 z .
That means the sides of the triangle have a ratio of A C : B C : A B = z : 2 z : ( 2 y + z ) = z : 2 z : 5 1 3 z , and the smallest z for all integer sides is z = 5 , making the perimeter z + 2 z + 5 1 3 z = 5 + 1 0 + 1 3 = 2 8 .