A star in a square

Let the sum of the areas of the yellow regions be $Y$ , the white areas be $W$ and the blue area be $B=12$ .

Let's add up the triangles ADF, ADE, DCG, ABG and the trapezium ECBF. This will count all the yellow areas once , as each yellow segment appears in one of the shapes listed, and it will also count all the white areas twice , as each white segment appears in two of the shapes listed. So: $\begin{aligned}Y+2W&=[ADF]+[ADE]+[DCG]+[ABG]+[ECBF]\\ &=\frac{1}{2}(12)AF+\frac{1}{2}(12)DE+\frac{1}{2}(12)CG+\frac{1}{2}(12)GB+\frac{12}{2}(EC+FB)\\ &=6(AF+DE+CG+GB+EC+FB)\end{aligned}$ But $AF+FB=12,DE+EC=12$ and $CG+GB=12$ , so $\begin{aligned}Y+2W&=6(12+12+12)\\ Y+W+W&=216\\ B+Y+W+W&=216+12=228\end{aligned}$ Now, $B+Y+W$ must equal $12^2$ , as all the areas added together make up the whole square. $\begin{aligned}144+W&=228\\ W&=84\end{aligned}$ Now we can determine the size of the yellow area: $\begin{aligned}Y+W+B&=144\\ Y+84+12&=144\\ Y&=48\end{aligned}$ So the answer is $\boxed{48}$

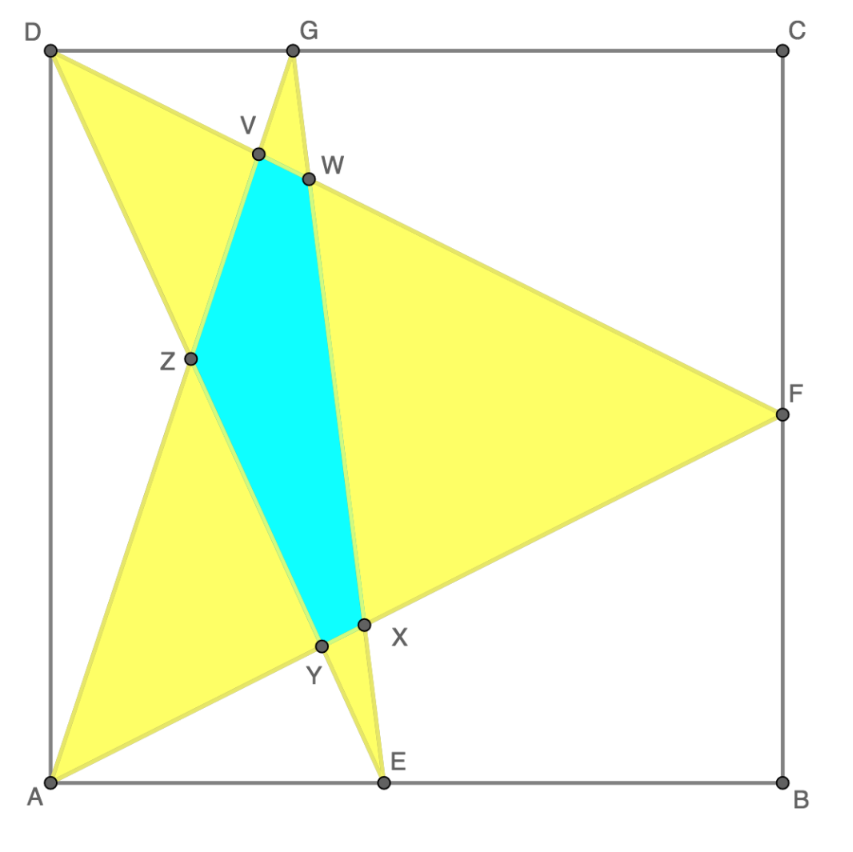
The area of the square is 144. If the yellow were a full triange (ΔAFD) then its area would be exactly half that (= 72).

Now, assume EG is vertical, so we can calculate for the symmetric case where ΔEZG is flipped into ΔAZD. The complete triangle ΔAFD (area 72) now has two chunks of blue cut out of it. So subtract 12 twice. Answer: 72 - (2 * 12) == 48

(I took a shortcut to assume symmetry here, without proof, because if asymmetry changed the answer then the problem wouldn't have a solution ... Edit: Thanks Pascal Engeler for the proof [in reply-comment])

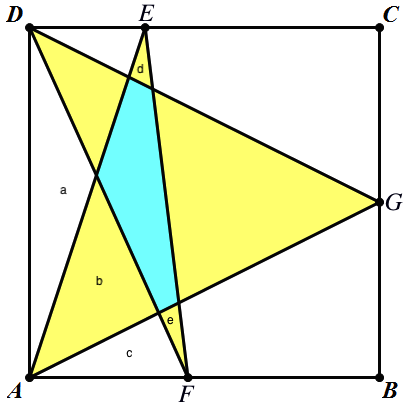First, thanks to Joseph Newton for the picture. After some dead-ends, I noted that triangles ADF and AEF have the same areas, as they share a base length and height. I've labelled the regions inside these triangles a through e.

The area of ADF is then a + b + c, and AEF is 12 + b +c + d + e.

Setting these equal, b and c cancel leaving a = 12 + d + e

The triangle ADG is half the square's area: 72, and to get the yellow area, a and 12 must be subtracted, and d and e added:

Yellow Area = 72 - (12 + d + e) - 12 + d + e = 72 - 12 -12 = $\boxed{48}$

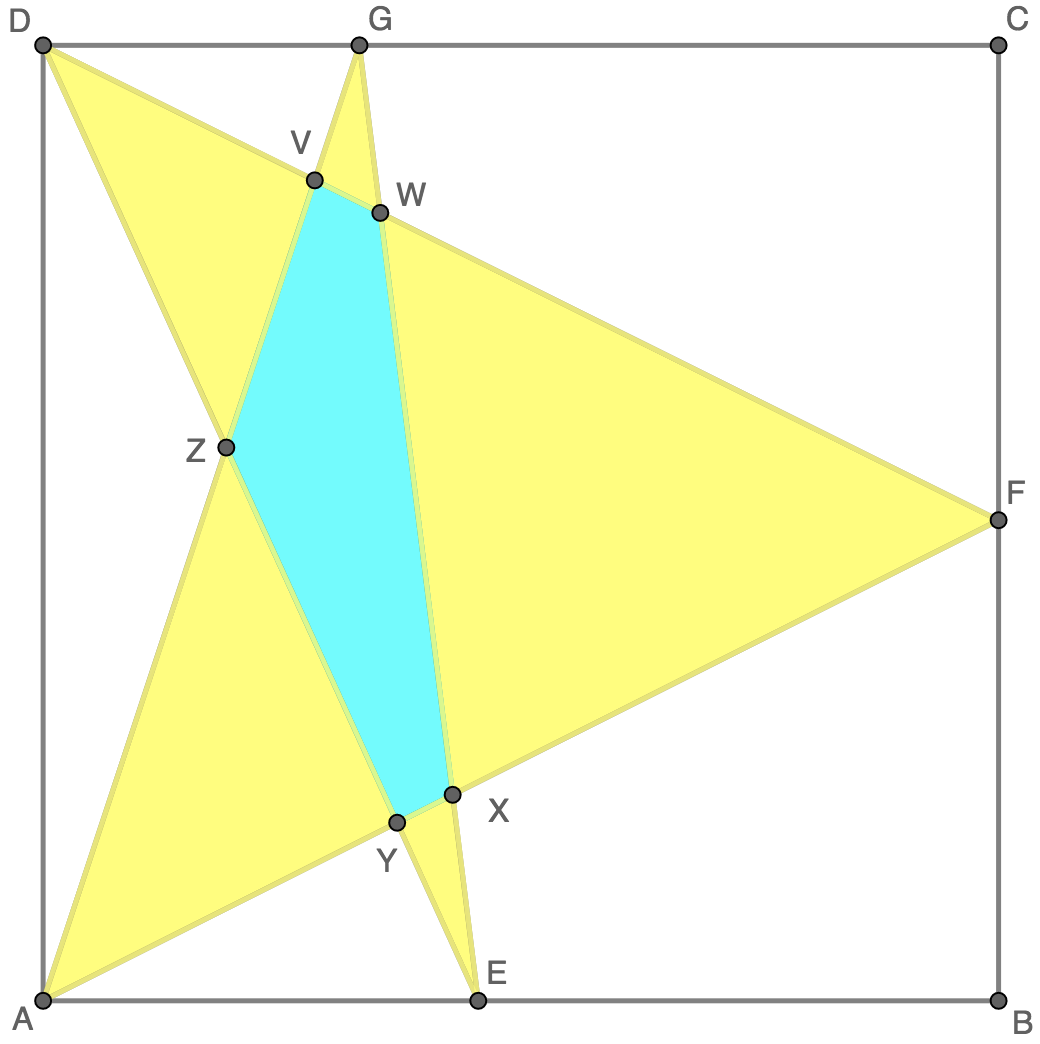
Label the points as shown above. Let $[A_1 A_2 \cdots A_n]$ denote the area of the polygon with vertices $A_1, A_2, \cdots, A_n.$ From the problem statement, we are given that $[VWXYZ] = 12$ and $[ABCD] = 12^2 = 144.$ Note that the area of $\triangle ADF$ is half of square $ABCD,$ so $[ADF] = \dfrac{1}{2}(12^2) = 72.$

Let $a = DZ, b = GZ.$ Since $\triangle AEZ \sim \triangle GZD,$ we have $EZ = rDZ = ra$ and $AZ = rGZ = rb$ for some positive real number $r.$ We can use these side lengths to find $[AZD]$ and $[EZG]$ :

$[AZD] = \dfrac{(AZ)(DZ) \sin \angle AZD}{2} = \dfrac{rab \sin \angle AZD}{2} \\ [EZG] = \dfrac{(EZ)(GZ) \sin \angle EZG}{2} = \dfrac{rab \sin \angle EZG}{2}.$

Since $\angle AZD = \angle EZG,$ we conclude that $[AZD] = [EZG].$

Let $K = [ZAY] + [YEX] + [XFW] + [WGV] + [VDZ]$ i.e. the area of the yellow region. Note that

$[AZDF] + [EZG] = ([ZAY] + [XFW] + [YEX] + [VDZ] + [VWXYZ]) + ([YEX] + [WGV] + [VWXYZ]) = K + 2(12) = K + 24.$

However, because $[EZG] = [AZD],$ we also have

$[AZDF] + [EZG] = [AZDF] + [AZD] = [ADF] = 72.$

Thus, $K + 24 = 72,$ or $K = \boxed{48},$ and we are done.

If you moved the smallest yellow triangles into the corresponding areas of the large white triangle, the resulting shape is the same as the blue pentagon so has an area of 12. (I had a diagram but it wouldn't let me insert it, sorry).

So because the yellow area plus the blue and the white version that we made in the last sentence, makes up half of the square, so overall 72.

Then minus the two lots of 12 from 72 and you get 48.

Well this is my attempt and I am not 100% sure about the first point but here it goes:

First, lets name the left vertex of the blue area $H$ It can be observed that the area of $DAH$ is equal to the area of $EHF$ . So let's shift $EHF$ into $DAH$

What we end up with is a triangle $DAG$ with a missing area in the middle which has the size of 12 (used to be the blue area). We also need to subtract the blue shifted area. So the yellow area will be the area of $DAG - 2 (12)$ Because of $[DAG] = (12 * 12)/ 2$ we end up with $(12 * 12)/ 2 - 2 * 12 = 4 * 12 = 48$