A steel ball in water
When placed on a scale, a container of water measures 2 0 kg , while a steel ball measures 2 kg . Now, the steel ball is dipped into the water, as shown in the diagram above. What will be the new reading on the scale?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
16 solutions
less than 22, because the volume is changing, not the weight.. the ball is suspended
Log in to reply
Are you suggesting that the reading will be equal to 2 0 kg ?
Log in to reply
I'd say so, Rohit. As the ball is not floating, the whole of its weight must be supported by the string.
Log in to reply
@Gabriel Colomer – What about the buoyant force? Will the water not exert a force on the steel ball?
Log in to reply
@Rohit Gupta – Oops... did not think about that! So, if the ball sinks in water and weighs 2kg, its volume must be less than 2 liters. Then, the bouyant force must be equally less than 2kg, and the rest is supported by the string.
Log in to reply
@Gabriel Colomer – Yes, some of the ball's weight is supported by the water and rest by the string.
the scale reads 0.
It reads a "steel ball in air weighs 2 kg." Doesn't that suggest the ball itself weighs 2 kg? That, of course, means the container would weigh greater than 22 kg.
Log in to reply
The ball do weigh 2 kg but how do you conclude that the container would weigh greater than 2 2 kg ?
I was thinking the ball (2 KG) + the weigh of the string/suspender. Maybe I'm looking at it wrong
Log in to reply
Why would the weight of the string add to the reading of the scale?
Log in to reply
@Pranshu Gaba As the ball is dipped in water, the weight from the string held by the suspender would add to it. However, once the ball stops moving, the force pulling the ball up would make it lighter than 22 KG.
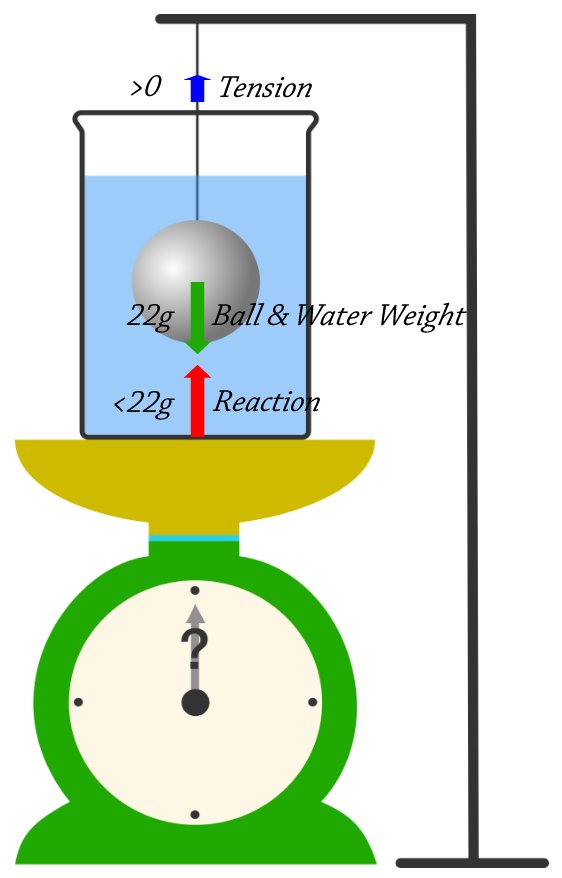Whatever the tension force is, it will reduce the reaction force from the scales to maintain equilibrium.
If you are talking of the Ball and water together as a system then Buoyant force is internal(water exerts on it so body exerts on the water as well).So then the weight recorded is 22kg(If no Tension).But a cleaner approach is that if we take the entire system then its being acted upon by Tension,Weight and Normal so the recorded weight is less than 22kg.Internal forces do not affect. From your reasoning the recorded weight is less than 22kg even if there is no string.Hope it helps.
Log in to reply
You're right, the buoyancy forces cancel out. Updated the solution:)
A more basic version is to consider water as a system.Then the forces are buoyant force.Lateral ones(nullified effect),Weight,Normal.So N = B + M g .Also B + T = m g for the ball.So B < m g .Hence you are left with N < ( M + m ) g
Log in to reply
We may also say that as the ball has a tendency to sink, the buoyant force acting on it must be smaller than its weight. According to the Newton's third law, an equal force (less than the weight of the steel ball) acts back on the water by the steel ball. Thus, the weighing machine feels a force smaller than the weight of 2 2 kg
... picture is wrong .... there is no 22g reaction on the scale ... you have the weight of the ball on the string and the buoyancy counteracts it ... resulting reaction force is on the ground ... ball could weigh 500kg and it would not make a difference.
Log in to reply
The picture says the reaction is less than 2 2 g and the tension is greater than 0. Although, you pointed out a good point that the reading won't be affected by the weight of the ball.
Log in to reply
... the 22g reaction on the scale is from the weight of the container and the water ... not the ball
Here is my simple explanation: The ball adds weight only equal to the amount of water it displaces. The ball raised the level of the water by an amount that equals its volume. So the increase in total weight is the weight of the water not the ball.
Log in to reply
I'm not sure if you are wholly right but, for me, this is the explanation that works best to my brain.
Drawing free body diagram and considering the forces
Let B be the force of buoyancy Then from equilibrium condition
N+B=22kg
Where N is normal reaction by weighting machine So N=22-B Since B>0 N<22
It seems to me that people are answering the wrong question. If the steel ball were resting on the bottom of the beaker, its weight would add to the weight of the water. But it isn't. It doesn't matter how much an ideal string weighs, but the fact is, the string is supporting the weight of the steel ball, minus the weight of the water it displaces. The displaced water weighs less than the steel ball, but it increases the height of the column of water. It increases the pressure on the bottom of the column, which is resting on the scale. So, the scale reads more than 20 kg, but less than 22 kg.
Log in to reply
I agree with you, the string carries some weight of the steel ball and hence the scale is not able to read its complete weight of 2 kg and the reading stands less than 2 2 kg and greater than 2 0 kg .
What would happen if the string wasn't because the ball was at a depth we're buoyancy equaled weight?
Log in to reply
Not sure if I understand your question. Buoyancy is the weight of the water displaced. Given the object is made of solid steel. the volume displacing the water will always be heavier than the water it displaces. Perhaps, if the sphere were hollow ...
If the steel ball floats and buoyancy equal the weight then the reading should be 2 2 kg .
If the steel is fully immersed into the beaker then the reading done by weighing pan will be 2 2 kg . as uprthrust will be zero. :)
Log in to reply
Upthrust acts even when a body is completely immersed in a liquid.
The upthrust will always be there its density×volume×g none of the quantities would be 0 Water will exert an upward force on ball which will lead to reduction in weight as g eff for it will be reduced
The upthrust will always be there its density×volume×g none of the quantities would be 0 Water will exert an upward force on ball which will lead to reduction in weight as g eff for it will be reduced
What about the weight of the wire holding the ball?
I thought mass was measured in kg not weight. Surely weight is a force and is measured in a different unit. The mass does not change.
Log in to reply
Yeah, surely the mass does not change but what about the reading of the scale?
Log in to reply
kg is incorrectly used here as synonym for 96.8kg
Log in to reply
@Avery Bentley Sollmann – I don't get you, can you elaborate more on your claim?
I agree with the solution of weight being less than 20 kg. But, cannot agree on the explanations given.
The ball is suspended by a rope and hence does not exert its weight on the scale. For example, if instead of water the fluid in the container was air.
In this case, the container + air inside would weigh say 100 gm and the ball weighs 2 kg. However, the suspended ball would not affect the scale reading.
This is not correct. The suspended ball is exerting a force in the downward direction on the water and hence on the scale. Increasing the reading beyond 2 0 kg . However, the force it exert is less than 2 kg therefore, the reading of the scale will be less than 2 2 kg .
Log in to reply
Does the string also support the water ontop of it? How would that affect the reading?
Surely it would read less to fill a bowl with some of the water and raise it above the water... how much weight is resupplied as such a bowl would be lowered by string into the water..
I would imagine the weight of the uplifted water by the suspended ball adds a similarly fractioned weight to the scale like the weight of the suspended ball does... I wonder the exact effect.
Log in to reply
The string does not exert any force on the water, the ball does. The ball applies a force equivalent to the buoyant force which does not depend on the depth at which the ball is kept unless you are considering the change in the density of water with the depth.
Log in to reply
@Rohit Gupta – Yes I mean does the water on top of the ball recieve and support from the ball below it (which is supported by the string)
Log in to reply
@Blood Blood – Yes, the ball will definitely support the water above it.
In this question, ball when is in air weighs 2kg. We know that, every fluid exerts a buoyant force. Buoyant force exerted by a fluid depends upon the density of fluid present. Water exerts more buoyant force than air because density of water is more than air. So when ball is dropped in water, water exerts a force on ball due to which weight of ball reduces. Weight of ball is now less than 2kg. Also, the weight of water container is 20 kg.
So , magnitude on weighing scale
= (20 + less than 2 kg)
=. Less than 22 kg but more
Than 20kg
What is the ball was made up of cork and floats on the surface without any string? Will the reading of the sale be 2 0 kg , 2 2 kg or in between them?
Log in to reply
Hm. I wonder if the cork resting above the water would allow air to support it, thus relieving some of the weight...
If not, by the common logic distrubited around here I would guess 22kg because the water still has to support the entire weight of the cork.
Log in to reply
Yes, the air will exert a buoyant force on the cork, we should neglect that otherwise the reading would be less than 2 2 kg .
This question is technically unanswerable by logical definition since the correct answer is greater than 20 kg and less than 22 kg since the ball is not floating. We know that the bouancy of the ball has a reaction force that is added to the weight of the system, but we don't know what it is. However, we do know that the ball is not floating so the bouancy is less than the balls mass. Please note also that the balls mass is greater than 2 kg since the ball does have a small bouancy in air.
The exact reading can be calculated if the volume of the ball and density of ball and water is given. However, with the data given we can surely say that the reading should be less than 2 2 kg .
To measure the weight of an object it must be kept on the weighing scale i.e., the surface of the object should be in contact with the surface of weighing scale, only then it will measure the weight of the object. In this case the steel ball is hung by a string and not touching the surface of the weighing scale so it will not measure it's weight and it will measure the weight of the container filled with water only which is 20kg which is less than 22kg.
I don't agree with you. The steel ball will exert some force on the water (equal to the buoyant force and less than its weight). The scale will read greater than 2 0 kg and less than 2 2 kg .
the actual ball isn't touching the surface between the scale and the container so its not added to the total weight of water
The weight of the ball is not on the scale because it is suspended by the string. Simple.
So, are you suggesting that the reading of the scale will be 2 0 kg ? If yes, then what about the buoyancy force?
According to Archemidis principles
Yes, by the Archimedes principle, the ball experiences an upthrust from the water, but by Newton's third law, the water experiences an equal downward force. Why would the reading not be 22 kg, but less than 22 kg?
Can you elaborate more on how Archimedes principle is used here to get the reading of the scale?
Not really part of the question, but isn't the actual weight simply the existing weight plus the weight of the water displaced by ball and string?
I don't understand what you're saying. Can you elaborate on what do you mean by actual weight and existing weight?
The weight of the ball is balanced by the tension in the string that is why it will not exert any force on the weighing machine because if the single weight is fully balanced by another single element than that weight will doesn't affect on remaining weights.
How can you say that the weight of the ball is fully balanced tension? What about the buoyant force of water?
The ball weighs 2kg and the water weighs 20kg so the response is at first to add the weights. But because of boyancy the ball is being pushed up, which makes it weigh less than 2kg. Thus, the answer is less than 22kg
The buoyancy force is less than 2 kg as the steel ball has a tendency of sinking. Although, the thread plays an important role as the rest of the weight of the ball is carried by it.
Bonus Question What will be the reading of the scale, if the ball is not attached to the thread and it is resting on the base of the container?
Gravitional force is 10N. 2×10.. 20 is less than 22
Can you elaborate on how the gravitational force is 1 0 N and why did you multiply it by 2?
Usually if you simply add the mass of the ball and the container..it would add upto 22kg.. but remember that the container is filled by a FLUID and therefore it will exert a bouyant force say "F" in the upward direction..
☝F
⚫
👇 mg
NET= mg - F
Therefore the net force exerted by the ball will less tham 2 kg.. hence the total weight of the system will be 20 + (<2) <22..i.e. less than 22kg
This is not clear to me. The weighing scale reads the normal force exerted by container on it. Why would the weight of the ball contribute to the normal reaction between the container and the weighing scale?
Tidal forces pay a miniscule role. The water is brought further away from the Earth via displacement and so the force of gravity on them is less and the reading on the scale is slightly almost immesurably less
The reading will be much smalIer than 2 2 kg . This question does not really ask for the tidal forces. The weight of the steel ball is not completely carried by the water, rather it is shared by the thread.
The total weight of the container, water and steel ball is 22kg. If any of this is borne by the string, the weight supported by the scales must be less than 22kg.