A strange octagon
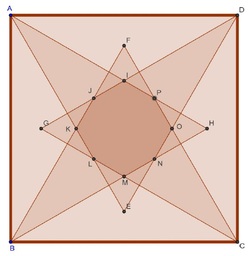 ABCD is a square with a side length of
3
3
.
AED, DGC, AHB and BFC are equilateral triangles.
ABCD is a square with a side length of
3
3
.
AED, DGC, AHB and BFC are equilateral triangles.
The area of the polygon IJKLMNOP is
a
+
b
3
, where
a
and
b
are rational numbers.
What is the value of
a
+
b
?
The answer is 36.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Mr. Munteanu, could you please check the answer of A Geometry problem by Marius Munteanu ? I've tried to answer, but the system said my answer was incorrect. Thanks...
Nice solution. when I solve it I considered the triangle FXG, X centre of the square . Then i found the area of triangles FXK, FXG, FJG andGXI. Then area of the the polygon IJKX= 2Area(FXK)+Area (FJG)-Area(FXG). Multiply that by 4 you will get the answer.
z = 2 QR = 2(BR - BQ) => z= 2 (3√3/2 - 3√3/(1+√3)) = 6√3 - 9, A=z^2 +(√3/4) z^2*(4/3) = 81 - 45√3
How to get angle MCR as 3 0 ∘ ? I got the interior angle of the polygon IJKLMNOP as 1 3 5 ∘ based on the fact it is an octagon and calculated RMC as 6 7 . 5 ∘ which lead to MCR being 2 2 . 5 ∘ . Where was I wrong? Thx. =)
Log in to reply
Δ CDG is an equilateral triangle, then it is obvious ∠ MRC = 3 0 ∘ .
It's not a regular polygon. Half the interior angles are 1 2 0 o (e.g. the angle at I ) and half are 1 5 0 o (e.g. the angle at J ).
In reply to @Patrick Corn and @Tunk-Fey Ariawan : Oops, I made some wrong assumptions. Thx guys, that was helpful. ;)
But I want to ask, how can I proof the polygon formed inside is a regular octagon?
Log in to reply
It is not a regular octagon. It has all the sides equal but not all the angles are equal. That is why I have call it a strange octagon.
Consider a coordinate system where the origin is the centre of the square. Find the equations of the following lines accordingly.

On solving them, you'll get O ( 2 3 9 − 3 3 , 0 ) , N ( 2 ( 3 + 1 ) 3 3 ( 3 − 1 ) , 2 ( 3 + 1 ) 3 3 ( 1 − 3 ) ) and M ( 0 , 2 3 3 3 − 9 ) . Due to symmetry, take the mirror image of N and M in the first quadrant as P ( 2 ( 3 + 1 ) 3 3 ( 3 − 1 ) , 2 ( 3 + 1 ) 3 3 ( 3 − 1 ) ) and I ( 0 , 2 3 9 − 3 3 ) .

Now, find the area of the shaded part for the first quadrant.
4 1 A = ( Z R × R P ) + ( 2 1 R P × R O ) + ( 2 1 W I × W P ) = ( Z R × R P ) + ( R P × R O ) = R P ( Z R + R O ) = ( R P × Z O ) ⟹ 4 1 A = 4 9 3 ( 3 3 − 5 ) ⟹ A = 8 1 − 4 5 3
So, 8 1 − 4 5 = 3 6
I also did with coordinate geometry.
If you have marked the origin Z , you could have rather found the area of Δ P Z O and multiplied it by 8, instead of the square + 2 triangles. This was what I did.
The octagon is big square s 2 = 2 7 minus 4 times yellow quadrangle, see geogebra illustration .
 illustration
illustration
Yellow quadrangle is sum of two similar blue triangles. Similarity coefficient of two blue triangles is easily calculated by dividing their black heights: 4 s 3 2 s − 4 s 3 = 3 2 − 3 . Bigger blue triangle is half of equilateral triangle: 8 s 2 3 . Adding smaller one gives their sum 8 s 2 3 ( 1 + 3 ( 2 − 3 ) 2 ) = 4 s 2 3 ⋅ 3 5 − 2 3 . 4 times yellow quadrangle is then s 2 3 ⋅ 3 5 − 2 3 = s 2 ⋅ 3 5 3 − 6 . The area of octagon is s 2 − s 2 ⋅ 3 5 3 − 6 = 9 ⋅ ( 9 − 5 3 ) = a + b 3 . The solution is a + b = 9 ⋅ ( 9 − 5 ) = 3 6 .
[ I J K L M N O P ] = 3 [ A H B ] − [ P H N ] H A H P = 2 + 3 1 = > [ A H B ] [ P H N ] = ( 2 + 3 1 ) 2 = > [ I J K L M N O P ] = [ P H N ] × ( 3 1 − 7 + 4 3 1 ) = > [ I J K L M N O P ] = 7 + 4 3 9 3 ( 1 + 3 ) = a + b 3 = > 7 a + 1 2 b = 2 7 , 4 a + 7 b = 9 = > a = 8 1 , b = − 4 5 = > a + b = 3 6 .
Let X be the centre of the square ABCD.
△
F
X
K
≡
△
G
X
I
(
∠
K
F
X
=
3
0
∘
)
Let
F
X
=
x
, then
K
X
=
F
X
/
3
=
3
x
F
G
=
2
x
J
Y
=
F
Y
⋅
tan
∠
J
F
Y
=
F
G
/
2
tan
1
5
∘
=
2
(
2
−
3
)
x
2
.
AREA(XKJI) = 2Area(FXK) + Area(FJG) - Area(FXG) = 2∙x^2/(2√3) + 1/2 ∙(x√2)/2(2-√3)∙ x√2 - x^2/2 =
=x^2 [√3/3+1/2(2-√3)-1/2]=27/4(4-2√3)(1/2-√3/6)=1/4(81-45√3)
Area(Octagon)= 4∙ AREA(XKJI)= 81-45√3→a+b=36
Isn't this the same question as strange octagon which you published some time back?
Log in to reply
Yes but I couldn't write(format) my solution for that one so I delete that one and write it again. Still the format of the solution is not as I would expected. I have written it in MsWord but it doesn't look too god. Any advice?
![]() profile pic
profile pic
Log in to reply
We are working on easier ways to share images, so that you can just take a screenshot of your work.
Currently, the simplest approach would be to take a screenshot, upload it (on Imgur or Flickr) and then use markdown code of ! [title] (link) with spaces removed. I've edited your comment, so you can look at it as an example.
Though, MsWord is not ideal for displaying equations. We use Latex, which makes the equations pretty. You can read up on it in the Math formatting guide .
Note: I've moved your solution over, and deleted the duplicate question.
Log in to reply
@Calvin Lin – Hi, I went to Latex and then I copied the equations from there, but it didn't looked too nice because it was copying the code from the bottom of the page.
Another question is how I can modify the answer to a posted question if I realize something isn't right?
Thank you for you help and patience ! Regards, Marius
Log in to reply
@Marius Munteanu – I have edited the first line of your solution, to give you an example of how Latex works. I don't fully understand what you mean in the first paragraph. Let me know if this helps.
We are working on giving members more control over the problem. In the meantime, you can send me an email ([email protected]), or reply to the clarification/dispute emails, if you want to update the answer to the question.
See the picture below.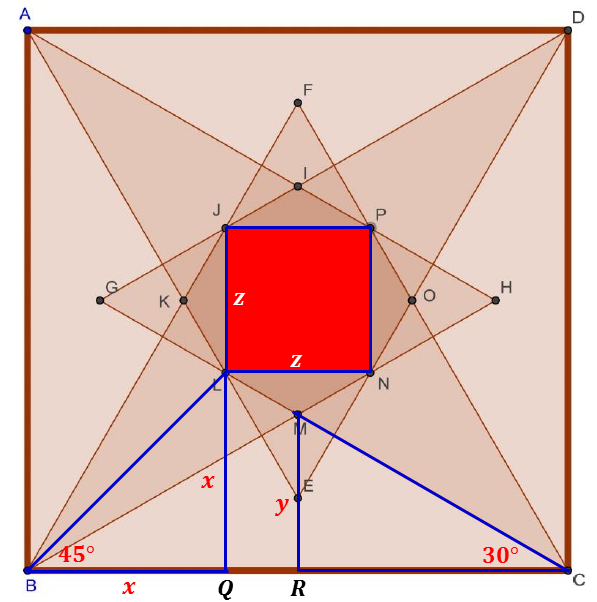 Octagon in Square
Using
Δ
MRC
:
M
R
y
=
R
C
tan
3
0
∘
=
2
3
3
⋅
3
1
=
2
3
.
Using
Δ
CQL
:
L
Q
x
x
3
+
x
x
=
Q
C
tan
3
0
∘
=
(
3
3
−
x
)
⋅
3
1
=
3
3
=
3
+
1
3
3
=
2
9
−
3
3
.
Then, we calculate length
L
N
.
L
N
z
z
=
B
C
−
2
B
Q
=
3
3
−
2
x
=
3
3
−
2
(
2
9
−
3
3
)
=
6
3
−
9
.
Therefore, area of the polygon
IJKLMNOP
is equal to the sum of the area square
JLNP
and four times area of the triangle
LMN
.
[
IJKLMNOP
]
=
[
JLNP
]
+
4
[
LMN
]
=
z
2
+
4
⋅
2
1
z
(
x
−
y
)
=
z
(
z
+
2
(
x
−
y
)
)
=
(
6
3
−
9
)
(
6
3
−
9
+
2
(
2
9
−
3
3
−
2
3
)
=
(
6
3
−
9
)
(
6
3
−
9
+
9
−
3
3
−
3
)
=
(
6
3
−
9
)
(
3
3
−
3
)
=
8
1
−
4
5
3
.
Thus,
a
+
b
=
8
1
+
(
−
4
5
)
=
3
6
.
Octagon in Square
Using
Δ
MRC
:
M
R
y
=
R
C
tan
3
0
∘
=
2
3
3
⋅
3
1
=
2
3
.
Using
Δ
CQL
:
L
Q
x
x
3
+
x
x
=
Q
C
tan
3
0
∘
=
(
3
3
−
x
)
⋅
3
1
=
3
3
=
3
+
1
3
3
=
2
9
−
3
3
.
Then, we calculate length
L
N
.
L
N
z
z
=
B
C
−
2
B
Q
=
3
3
−
2
x
=
3
3
−
2
(
2
9
−
3
3
)
=
6
3
−
9
.
Therefore, area of the polygon
IJKLMNOP
is equal to the sum of the area square
JLNP
and four times area of the triangle
LMN
.
[
IJKLMNOP
]
=
[
JLNP
]
+
4
[
LMN
]
=
z
2
+
4
⋅
2
1
z
(
x
−
y
)
=
z
(
z
+
2
(
x
−
y
)
)
=
(
6
3
−
9
)
(
6
3
−
9
+
2
(
2
9
−
3
3
−
2
3
)
=
(
6
3
−
9
)
(
6
3
−
9
+
9
−
3
3
−
3
)
=
(
6
3
−
9
)
(
3
3
−
3
)
=
8
1
−
4
5
3
.
Thus,
a
+
b
=
8
1
+
(
−
4
5
)
=
3
6
.