A 'Trap'ezium
A B C D is a trapezium with A B ∣ ∣ C D and its diagonals intersect at M such that ∠ A M D = 6 0 ∘ .
O is the centre of the circle passing through A B C D such that O M = 2 .
∣ A B − C D ∣ = m n find m + n
Note : m and n are integers and n isn't a perfect square.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice solution via coordinate geometry
As the trapezium is cyclic, it is also isosceles.
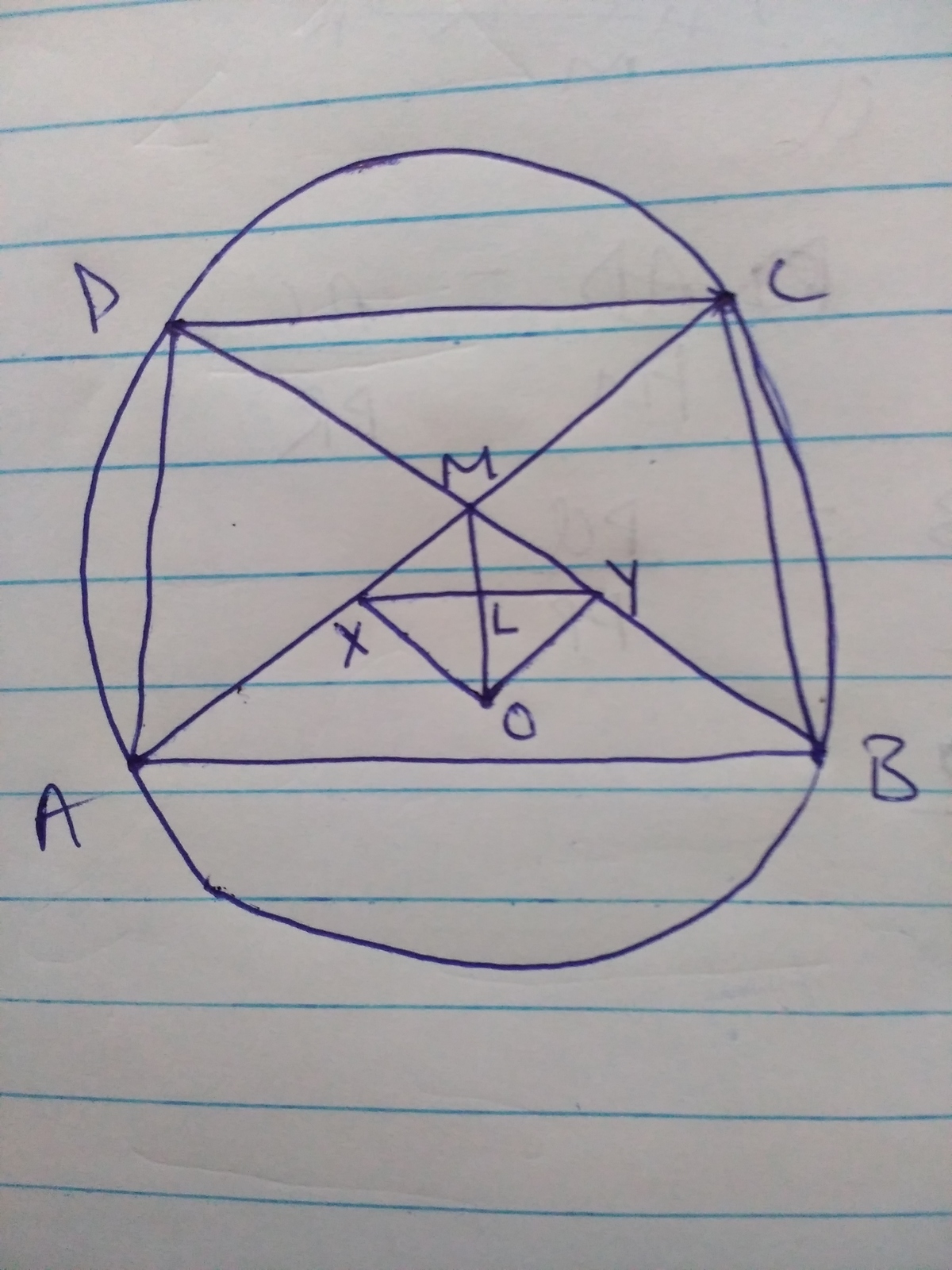
Let X and Y be midpoints of diagonals A C and B D respectively.
X Y intersects O M at L
Join O X and O Y .
O X and O Y are perpendicular to A C and B D ( Why? )
Angle X M Y = 1 2 0 ° , So angle X M O = Angle Y M O = 6 0 ° (By symmetry)
In ∆ O X M , s i n M = s i n 6 0 ° = 2 O X = 2 3
O X = 3 , so, X M = 1
O M is perpendicular to X Y (By symmetry)
So, we get X L = Y L = 2 3 , so, X Y = 3
We know that ∣ A B − C D ∣ = 2 × X Y
So, answer us 2 3
n + m = 2 + 3 = 5
This problem is from the 2007 RMO.
You have given O M as 2 and by that, the answer is coming out to be 6 thus m + n = 1 + 6 = 7 .
You should consider correcting either the value of O M or your answer.
Log in to reply
Sorry for the inconvenience, I meant OM=2. Did you clear this year's RMO?
Log in to reply
I did not give it. I don't satisfy the age criteria ;(
Log in to reply
@Vedant Saini – Aren't you 14? Class 8/9?
Log in to reply
@Mr. India – No, there wasn’t any option of my age when I set my age on brilliant. That’s why it is 14
A cyclic trapezium is also an isosceles trapezium, and by symmetry the center of the circle must be on the perpendicular bisector of the bases of the trapezium. Since O M = 2 , place the trapezium on a coordinate plane so that the center of the circumscribed circle is at the origin and M is at ( 0 , 2 ) .
Since ∠ A M D = 6 0 ° , ∠ D M C = 1 8 0 ° − 6 0 ° = 1 2 0 ° , and since △ D M C is an isosceles triangle, ∠ M D C = ∠ M C D = 2 1 8 0 ° − 1 2 0 ° = 3 0 ° . This means the slope of B D is tan 3 0 ° = 3 3 , and since its y -intercept is 2 the equation of its line is y = 3 3 x + 2 . Likewise, the slope of A C is tan 1 5 0 ° = − 3 3 , and since its y -intercept is 2 the equation of its line is y = − 3 3 x + 2 .
Let a be the x -coordinate of B . Since B is on y = 3 3 x + 2 , its coordinates are ( a , 3 3 x + 2 ) . Using the distance between B and the origin gives the radius r of the the circle, so r 2 = a 2 + ( 3 3 x + 2 ) 2 , which makes the equation of the circle x 2 + y 2 = a 2 + ( 3 3 x + 2 ) 2 .
C is on both the circle x 2 + y 2 = a 2 + ( 3 3 x + 2 ) 2 and on the line y = − 3 3 x + 2 , and combining these equations to eliminate y gives an x -coordinate of x = a + 3 .
By symmetry, if a is the x-coordinate of B , then A B = 2 a , and if a + 3 is the x -coordinate of C , then C D = 2 a + 2 3 . Therefore, ∣ A B − C D ∣ = ∣ 2 a − ( 2 a + 2 3 ) ∣ = 2 3 , so m = 2 , n = 3 , and m + n = 5 .