A Triangle and Two Regular Convex Polygons
An equilateral triangle and 2 other regular polygons share a single vertex in such a way that the three shapes completely cover the 3 6 0 ∘ of space surrounding the vertex without overlapping.
What is the largest possible number of sides that one of the regular polygons can have?
An equilateral triangle, regular 9-gon, and regular 18-gon can cover all
3
6
0
∘
around a single vertex. Is 18 the maximum number of sides one of these regular polygons can have?
The answer is 42.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
Great solution!
Can u prove that exterior angle of a regular n hon is 360/n ?.I know it is but please provide a proof
Log in to reply
Start on a side of the polygon and travel around its perimeter. At every vertex, you'll turn over an angle α . When you return at your starting point, you have turned over an angle n α . You have also turned a whole angle. Thus n α = 3 6 0 ∘ .
Or, connect each of the vertices to the center of the polygon. By symmetry, the central angle is divided into n angles of 3 6 0 ∘ / n . Each of the triangles that is formed is isosceles, with base angles 2 1 ( 1 8 0 ∘ − 3 6 0 ∘ / n ) . At each vertices two of these angles meet, making an internal angle of 1 8 0 ∘ − 3 6 0 ∘ / n .
Log in to reply
the first one proof is gold
Also for a non-regular n-agon the interior alngles sum up to 180(n-2) in a similar way :)!
But why is it that we are taking any arbitrary polygon yet after a complete rotation we come up to 360 degree??
Log in to reply
@Erica Phillips – Consider a circle with a horizontal tangent across the top. Slide the tangent completely around the circle in either direction, until you arrive back at the starting point. The tangent has rotated 360 degrees. Now take an arbitrary polygon and lay a straight line flat against one edge. “Click” the straight line around to the next flat edge, and to the next, and to the next, until you arrive back at the edge where you started. The rotation wasn’t a smooth glide as it was with the circle - rather a series of “clicks” - but the result is exactly the same. The straight line has rotated 360 degrees. For a square, there are four clicks of 90 degrees apiece; for a decagon, there are 10 clicks of 36 degrees apiece. For an irregular polygon, the magnitude of the individual clicks will vary, but they will always sum to 360 after a complete rotation around the figure.
Log in to reply
@Albert Fisher – Thanks a lot for this wonderful explanation!!!
Maybe this is only a coincidence, but the Hitchhiker's Guide to the Galaxy returns to BBC radio 4 this week!
Log in to reply
I almost titled this question, "The Answer to the Great Question Of Life, the Universe, and Everything" :-)
The factorization 3 6 = ( n 1 − 6 ) ( n 2 − 6 ) shows that there are only five such arrangements involving equilateral triangles, one for each of the five positive factor pairs of 36.
3 6 = 1 ⋅ 3 6 ⇒ n 1 = 7 , n 2 = 4 2 a heptagon and a 42-gon
3 6 = 2 ⋅ 1 8 ⇒ n 1 = 8 , n 2 = 2 4 an octagon and a 24-gon
3 6 = 3 ⋅ 1 2 ⇒ n 1 = 9 , n 2 = 1 8 a nonagon and an 18-gon
3 6 = 4 ⋅ 9 ⇒ n 1 = 1 0 , n 2 = 1 5 a decagon and a 15-gon
3 6 = 6 ⋅ 6 ⇒ n 1 = 1 2 , n 2 = 1 2 two dodecagons
If you generalize the problem to three regular polygons meeting at a point (but don't require one to be a triangle: n 0 = 3 ), there are these five arrangements and five more. They can be found similarly to Arjen's method. Just consider the additional cases of n 0 = 4 , 5 , 6 separately. One of the regular polygons must have 6 or fewer sides (otherwise all have interior angles greater than 1 2 0 ∘ ), so we can stop at n 0 = 6 .
n 0 = 4 , n 1 = 5 , n 2 = 2 0 a square, a pentagon, and a 20-gon
n 0 = 4 , n 1 = 6 , n 2 = 1 2 a square, a hexagon, and a dodecagon
n 0 = 4 , n 1 = 8 , n 2 = 8 a square and two octagons
n 0 = 5 , n 1 = 5 , n 2 = 1 0 two pentagons and a decagon
n 0 = 6 , n 1 = 6 , n 2 = 6 three hexagons
Log in to reply
A comprehensive article on tiling regular polygons can be find here .
Log in to reply
Of course, "tiling" requires that the pattern can be continued indefinitely... there has to be a global symmetry of the plane, not just internal angles that add up to 3 6 0 ∘ . That makes for a very different problem than the current question.
Log in to reply
@Arjen Vreugdenhil – The article includes a list of 3 regular polygons that can meet at 1 vertex, including the one given in the current question, but as an "unusable" tiling.
Log in to reply
@David Vreken – Very interesting. It looks like there is a pretty easy test to determine if a vertex is usable for a tiling. The vertex must have either a) three even polygons, or b) one odd polygon and two identical even polygons.
a) 4-6-12, 4-8-8, 6-6-6
b) 3-12-12
Ok I’m new to this, so can someone explain what is wrong with my solution? As the number of sides increases on a polygon, the closer the angles get to 180degrees. If we say we have an infinity-gon with exactly 180degrees, and add that to the 60deg of our equilateral triangle, there are 120deg left, which is exactly the angle of a hexagon. Is this just a problem with using infinity or...?
Log in to reply
The "infinity-gon" is not a regular polygon, so you have to find the next solution, which happens to be a heptagon (one more side than the hexagon you found) and a 42-gon.
If a regular hexagon is tangent to a circle in one its vertices, one can indeed precisely wedge in an equilateral triangle. In that sense your approach corresponds to a real geometric configuration. However, a circle is not a polygon.
Your approach corresponds to a "factoring" of 3 6 = ( n 1 − 6 ) ( n 2 − 6 ) = 0 ⋅ ∞ . But ∞ is not a number and an ∞ -gon is not a polygon.
I tried the same way but by taking the interior angles as [(n-2)*180]/n. In the end I got the equation 3n+3n'-5nn'=12 Can you help me with it. Thanks!
Log in to reply
n ( n − 2 ) 1 8 0 = n 1 8 0 n − 3 6 0 = 1 8 0 − n 3 6 0 (after distributing). Now you have the starting terms of @Arjen Vreugdenhil 's solution, and hopefully you are able to follow it from there.
Log in to reply
Yeah I figured that much but I was just curious that is there any way to solve the equation I got??
Log in to reply
@Shanu Jindal – To solve 3 n + 3 n ′ − 5 n n ′ = 1 2 , note that − 5 ( n − 5 3 ) ( n ′ − 5 3 ) = − 5 n n ′ + 3 n + 3 n ′ − 5 9 . Therefore your equation becomes − 5 ( n − 5 3 ) ( n ′ − 5 3 ) = 1 2 − 5 9 = 5 5 1 . This equation has infinitely many solutions. The real solutions form an orthogonal hyperbola in the ( n , n ′ ) plane, with asymptotes at n , n ′ = 5 3 .
If you only want integer solutions, multiply both sides by − 5 to obtain ( 5 n − 3 ) ( 5 n ′ − 3 ) = − 5 1 . Factoring gives − 5 1 = − 5 1 ⋅ 1 = − 1 7 ⋅ 3 = − 3 ⋅ 1 7 = − 1 ⋅ 5 1 . Only − 3 and 1 7 are of the form 5 k − 3 for some integer k ; thus we find { 5 n − 3 = − 3 5 n ′ − 3 = 1 7 ∴ { n = 0 n ′ = 4
When n2 is infinite (polygon is a circle), n1 =6 a hexagon. My answer was that an infinite number of sides is the maximum that meets the criterion ...
Log in to reply
A circle is not a polygon, though. It is only the limit of a series of polygons.
i think the number is infinite....
Log in to reply
Infinity is not a number, an an ∞ -gon is no longer a polygon.
The polygon with fewer sides must have an exterior angle less than 60 degrees (the angle of the equilateral triangle), and the closer it is to 60 the smaller the contribution from the second polygon, and so the more sides it will have.
A hexagon has an external angle of exactly 60 degrees, so the first polygon must have seven sides with external angle 3 6 0 / 7 (about 51.4...)
The second polygon has an external angle of 6 0 − 3 6 0 / 7 (8.57...) so the number of sides is 3 6 0 / ( 6 0 − 3 6 0 / 7 ) = 42
Excellent solution!
Log in to reply
Thank you. Excellent question — possibly the Ultimate Question of Life, the Universe and Everything?
Let m be the number of sides of one of the regular convex polygons, and n be the number of sides of the other regular convex polygon. Then each of their interior angles are m π ( m − 2 ) and n π ( n − 2 ) , respectively, and the interior angle of the equilateral triangle is 3 π . In the given problem, all three of these interior angles must add exactly to the space surrounding a point, which is 2 π , and so m π ( m − 2 ) + n π ( n − 2 ) + 3 π = 2 π , and this simplifies to m = n − 6 6 n .
Since m = n − 6 6 n , m > 0 only when n > 6 . Therefore, since m > 3 (since m represents a side of a regular convex polygon), n > 6 . Also, since m ’ = ( n − 6 ) 2 − 3 6 < 0 , it is always decreasing, which means that the maximum possible m value occurs at the first possible n value after n > 6 , and since n is an integer (since n represents a side of a regular convex polygon), this is when n = 7 . Therefore, the largest number of sides is m = 7 − 6 6 ⋅ 7 = 4 2 .
Good problem! My approach was almost identical, except for the last part:
m = n − 6 6 n
There is a very simple (but maybe not obvious?) way of finding integer solutions to this type of equation:
m = n − 6 6 n − 3 6 + 3 6 = n − 6 6 ( n − 6 ) + 3 6 = 6 + n − 6 3 6
It is now easy to see that the maximum value for n which gives us an integer solution for m is when n − 6 = 3 6 , i.e. n = 4 2
Log in to reply
Nice! @Max Patrick had a similar solution to yours.
Sorry, probably it's that I'm not specialy farmiliarized with english lenguage but i didn't undertanded the problem well. I think the final question is not very specific. I thought that it was asking for a much more general question, the maximum number of sides a polygon could be so that there were some other polygons (any number or size of them) that could be arranged as such.
I don't if know I've explained well my confusion but the fact is that after a non-proportional effort to an intermediate problem I end up with the same solution! And I'm pretty sure that it's correct I mean n 1 = 3, n 2 = 7, n_3 = 42 is the optimal arrangement for any set of polygons! Maybe 42 is definitely the solution to the Ultimate Question of Life, the Universe and Everything:).
Anyway I think changing only "What is the largest possible number of sides that one of the regular polygons can have?" for "What is the largest possible number of sides that one (of the other two) regular polygons can have?" would be enough for a better understanding. Or maybe you could add a bonus question to the generalization I've tryed to explain a bit here. Thanks and nice problem.
The 3 internal angles sum to 360deg. The two unknown polygons are an m-gon and an n-gon.
(180m-360)/m + (180n-360)/n + 60 = 360 in degrees.
Boils down to mn - 6m = 6n m = 6 + 36/(n-6) The highest n such that m is an integer is n=42. m=7.
Answer is 42 sides.
Another good solution!
Consider the following implications :-
-
The sum of interior angles of the two polygons is 360 -60 = 300 degrees.
-
No interior angle can be greater than or even equal to 180, as minimum possible exterior angle for a polygon (with infinite sides) is 0 degrees, as i n f i n i t e n o . o f s i d e s 3 6 0 = 0
Therefore, The two conditions for two respective interior angles A and B are
A + B = 300 degrees
A , B < 180 degrees
Let us suppose one of them is 180 degrees, ie A = 180 degrees, then B = 300 - 180 = 120 degrees.
Interior angle for a polygon with n no. of sides = n 1 8 0 ∗ ( n − 2 ) = 120 , which yields n = 6 Therefore, when no of sides of one polygon is maximum, the minimum no. of sides for another polygon can only be 6. But we cannot have infinite sides on any polygon, so
Let us take the next minimum number of sides on the other polygon , 7; Interior angle of a polygon with 7 sides = 7 1 8 0 ∗ 5 , hence the interior angle for the second maximum no of sides of a polygon would be = 300 - 180 7 5
= 7 2 1 0 0 − 9 0 0
= 7 1 2 0 0
Now, n 1 8 0 ∗ ( n − 2 ) = 7 1 2 0 0
Therefore, n n − 2 = 2 1 2 0 , which yields n = 42
Nicely done!
Log in to reply
Thanks :) .... I didn't know the formula, so tried to solve it some way or the other.
Let n be a side of the orange regular polygon and m a side of the green regular polygon.
6 0 + n n − 2 1 8 0 + m m − 2 1 8 0 = 3 6 0 ⟹ n n − 2 + m m − 2 = 3 5 ⟹ n m n + m = 6 1 ⟹ 6 n = m ( n − 6 )
⟹ m = n − 6 6 n ,where n > 6 .
For n > 6 , the sequence m ( n ) = n − 6 6 n is monotonic decreasing ∴ the maximum occurs when n = 7 and m ( 7 ) = 4 2
As the interior angles of a regular polygon (the interior angle represented by a) must fit: a < 180 Then we must find the largest interior angle shape. We look through what it can be, and the first polygon that fits is a heptagon, with its interior angles being 7 ( 7 − 2 ) ∗ 1 8 0
From here, we know that the current angle total we have is about 188.57142 degrees.
We subtract this from 360, giving 171.42857 degrees per each interior angle of this shape.
To find the number of sides this shape has, we first figure out the exterior angles, by doing 180-171.42857=8.57143
Since exterior angles add up to 360, we can figure out how many exterior angles there are, by doing 8 . 5 7 1 4 3 3 6 0
This gives us 42 exterior angles, which is by extension 42 sides.
Good solution!
The external angles (i.e. 180 - internal angle) of the polygons have to sum to 60 degrees i.e. internal angle of the triangle. The external angle of an n sided polygon is 360/n degrees. Hence
n
3
6
0
+
m
3
6
0
=60 where n and m are integers representing the number of sides of the two polygons. Thus
n
1
+
m
1
=
6
1
. Clearly n and m MUST both be larger than 6 for this equation to hold. So if n=7 then m=42. If n=8 then m=24 all the way to n=42 and m=7. So as one number increases, the other decreases. Hence the largest polygon will have n or m =42 sides.
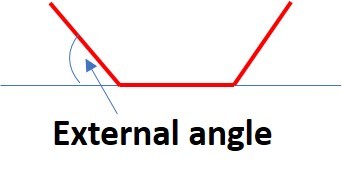
Great solution!
Log in to reply
I am trying to figure out how to include a diagram to show exactly how I define an "external" angle just in case some people don't understand what I mean by that term. But for some reason the system is not showing my diagrams...........Ahh. Got it to work!!!
N1 = 6 and N2 = infinity works too.
If the number of sides approaches infinity, then the shape would be a circle, not a regular polygon, and can be ruled out as an option.
Log in to reply
Does the definition of a regular polygon have a limit on the number of sides it can have?
Log in to reply
Yes - "in elementary geometry, a polygon is a plane figure that is bounded by a finite chain of straight line segments closing in a loop to form a closed polygonal chain or circuit".
We have two regular polygones and a triangle, where the contribution of their angles are
6 0 ∘ + ( 1 8 0 ∘ − 3 6 0 ∘ / n 1 ) + ( 1 8 0 ∘ − 3 6 0 ∘ / n 2 ) = 3 6 0 ∘ .
It is clear that, when n 1 increases, then n 2 decreases. Moreover, they follow
n 1 = 6 1 n 2 − 1 n 2 .
The limiting case is when n 1 → ∞ , i.e. a circle, in that case, the sum of the angles would be 6 0 ∘ + 1 8 0 ∘ + 2 4 0 ∘ = 3 6 0 ∘ , where 2 4 0 ∘ corresponds to n 2 = 6 . Therefore, the solution is the pair corresponding to the next integer, i.e. n 2 = 7 and n 1 = 4 2 ; the sum of the angles would be 6 0 ∘ + 1 7 1 . 4 3 ∘ + 1 2 8 . 5 7 ∘ = 3 6 0 ∘ .
Good solution!
The total angle of the two remaining polygons must be 300. No shape can have an angle greater than or equal to 180 (without having an infinite number sides which is impossible). Therefore we can deduce that the shape with the fewest number of sides must have more than 6 sides (as a shape with 6 sides has angles of 120 degrees which would leave 180 degrees remaining)
We have already been shown that an 8 side shape will work so we only have to test with a 7 sided shape.
The angle in a heptagon is roughly 128.5. Therefore the other shape must have angles of 300-128.5= 171.5 degrees The total angle of this shape is therefore the number of sides (n) multiplied by 171.5 However we also know that the total interior angle of a polygon is 180(n-2)
Set these equations as equal to each other and solve 171.5n = 180(n-2)
171.5n = 180n - 360
360 = 8.5n
42.3...= n
Therefore the larger number of sides is 42
Nice thinking! It would be better to express the interior angle of the heptagon as a fraction ( 1 2 8 7 4 ) so that later on you get the exact answer of 42, instead of an approximate answer of 42.3.
Consider the regular triangle, n 1 -gon, and n 2 -gon. The sum of their internal angles is ( 1 8 0 ∘ − 3 3 6 0 ∘ ) + ( 1 8 0 ∘ − n 1 3 6 0 ∘ ) + ( 1 8 0 ∘ − n 2 3 6 0 ∘ ) = 4 2 0 ∘ − n 1 3 6 0 ∘ − n 2 3 6 0 ∘ . This must be equal to 3 6 0 ∘ ; thus we have n 1 3 6 0 ∘ + n 2 3 6 0 ∘ = 6 0 ∘ . Divide by 6 0 ∘ and multiply by n 1 n 2 to find 6 ( n 1 + n 2 ) = n 1 n 2 ∴ n 1 n 2 − 6 ( n 1 + n 2 ) = 0 . Complete the product: ( n 1 − 6 ) ( n 2 − 6 ) = 3 6 . The factoring of 36 with the highest factor is 1 ⋅ 3 6 = 3 6 , so that n 1 − 6 = 1 and n 2 − 6 = 3 6 . This shows that n 1 = 7 and n 2 = 4 2 .