A Triangle's Stars Align
The vertices of a triangle are reflected about the opposite sides, and the resulting three points are collinear, also one of these three points is the midpoint of the other two.
The tangent of the smallest angle of this triangle is r p − q , for positive coprime integers p , q , r .
Submit p + q + r .
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Its interesting to note that one of the angles of the triangle is 4 5 ∘
Log in to reply
I knew that from the paper, but did not just want to quote it... I have added another calculation.
I also found out the fact that if a certain triangle's reflection triangle is degenerate, then the nine-point centre of the original triangle lies on the circumcircle of the original triangle.
And in this particular problem, one of the reflection vertex (the one in the middle) also lies on the nine point circle.
Log in to reply
The pedal triangle of a point is degenerate precisely when the point is on the circumcircle of the triangle (Wallace-Simpson Theorem).
Note that cos 2 θ = 4 1 ( 1 + 7 ) and sin 2 θ = 4 1 ( 7 − 1 ) , so that cos 2 θ = sin 2 θ + 2 1 . If we set the circumcentre O as the origin, the position vectors of A , B , C all have length R , the circumradius. Since the angle C is 4 1 π , we deduce that ∠ A O B = 2 1 π , so that a ⋅ b = 0 . Similarly we can show that a ⋅ c = − R 2 sin 2 θ and b ⋅ c = R 2 cos 2 θ .
Consider the point X with position vector x = 4 1 ( a + b ) + c = 4 1 ( h + 3 c ) , where h = a + b + c is the position vector of the orthocentre of A B C . Note that X lies on C H , with H X : X C = 3 : 1 . We calculate that ( x − a ) ⋅ ( x − c ) = 1 6 1 ( − 3 a + b + 4 c ) ⋅ ( a + b ) = 4 1 R 2 ( cos 2 θ − sin 2 θ − 2 1 ) = 0 so that X is the position vector of H C , the foot of the altitude from C . Thus the midpoint of H C is the reflection of C in A B , namely the point C ′ . But the nine-point circle passes through the midpoints of A H A , B H B and C H C , so (in particular) passes through the relection point C ′ .
Other points are noteworthy. Again, the fact that C = 4 1 π tells us that the triangle H A H B H C is right-angled, with the right angle at the vertex H C . This means that the nine-point centre (with is the circumcentre of H A H B H C ) is the midpoint of H A H B . Moreover the diameter of the nine-point circle passing through C ′ is perpendicular to the diameter H A H B .
Log in to reply
Wow, this triangle has some remarkable properties. It would be nice if you incorporate this into your solution and add a corresponding figure, so that everyone can see this.
Let △ A B C be the triangle and let it be scaled so A C = 1 . Place A at ( 0 , 0 ) , C at ( 1 , 0 ) , and B in the first quadrant, and let m = tan A and n = tan B .
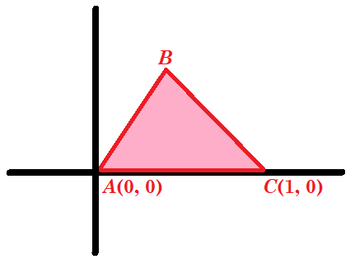
Then A B is on y = m x and B C is on y = − n ( x − 1 ) , and the intersection of these two lines is at B ( m + n n , m + n m n ) , which makes the reflection of B in side A C is at B ′ ( m + n n , − m + n m n ) .
Let the reflection of C in side A B be C ′ . Then A C = A C ′ = 1 , so that C ′ is on x 2 + y 2 = 1 , and C ′ is also on y = − m 1 ( x − 1 ) , the line perpendicular to A B through C . These equations solve to C ′ ( m 2 + 1 1 − m 2 , m 2 + 1 2 m ) .
Let the reflection of A in side B C be A ′ . Then C A = C A ′ = 1 , so that A ′ is on ( x − 1 ) 2 + y 2 = 1 , and C ′ is also on y = n 1 x , the line perpendicular to B C through A . These equations solve to A ′ ( n 2 + 1 2 n 2 , n 2 + 1 2 n ) .
If the reflected points are collinear and one point is the midpoint of the other two, then either:
A ′ is the midpoint of B ′ and C ′ :
Then m + n n + m 2 + 1 1 − m 2 = n 2 + 1 4 n 2 and m + n − m n + m 2 + 1 2 m = n 2 + 1 4 n , which has solutions ( m , n ) of ( 0 , 0 ) , ( − 1 , 3 ± 7 + 2 ) , and ( 1 , 3 ± 7 − 2 ) .
B ′ is the midpoint of A ′ and C ′ :
Then n 2 + 1 2 n 2 + m 2 + 1 1 − m 2 = m + n 2 n and n 2 + 1 2 n + m 2 + 1 2 m = m + n − 2 m n , which has solutions ( m , n ) of ( 0 , 0 ) , ( 3 − 7 − 2 , 3 7 − 2 ) , ( 3 − 7 + 2 , 3 7 + 2 ) , ( 3 7 − 2 , 3 − 7 − 2 ) , and ( 3 7 + 2 , 3 − 7 + 2 ) .
C ′ is the midpoint of A ′ and B ′ :
Then n 2 + 1 2 n 2 + m + n n = m 2 + 1 2 ( 1 − m 2 ) and n 2 + 1 2 n + m + n − m n = m 2 + 1 4 m , which has solutions ( m , n ) of ( 0 , 0 ) , ( 3 ± 7 − 2 , 1 ) , and ( 3 ± 7 + 2 , − 1 ) .
All cases result in either a degenerate triangle ( ( m , n ) = ( 0 , 0 ) ) or a reflection/rotation of a triangle with angles of approximately 1 2 . 1 5 ° , 4 5 ° , and 1 2 2 . 8 5 ° , the smallest of which has a tangent of m = 3 7 − 2 . Therefore, p = 7 , q = 2 , r = 3 , and p + q + r = 1 2 .
As in my solution to the previous problem concerning the reflection triangle, the reflection triangle A ′ B ′ C ′ is homothetic to the pedal circle N A N B N C of the nine-point circle, and this latter triangle has edge lengths U , V , W , where U V W = = = 1 6 v w P 1 6 u v Q 1 6 u v R P Q R = = = ( u − v ) 3 + ( u − w ) 3 + v w ( 3 u + v + w ) − u 3 ( v − u ) 3 + ( v − w ) 3 + u w ( u + 3 v + w ) − v 3 ( w − u ) 3 + ( w − v ) 3 + u v ( u + v + 3 w ) − w 3 where a = u , b = v , c = w are the sides of the original triangle. We want to find triangles A B C such that N C is the midpoint of N A N B , and hence such that 4 U = 4 V = W , so we want 4 u P = 4 v Q = w R . Define (scaling the calculations with u = 1 ) A 1 ( v , w ) = ( w R − 4 u P ) ∣ ∣ ∣ u = 1 A 2 ( v , w ) = ( w R − 4 v Q ) ∣ ∣ ∣ u = 1 Then we have A 1 ( v , w ) = A 2 ( v , w ) = 0 . We can write A 1 ( v , w ) − A 2 ( v , 2 ) = ( v − 1 ) A 3 ( v , w ) A 3 ( v , w ) = − w 3 + 3 ( v + 1 ) w 2 − ( 3 v 2 + v + 3 ) w + v 3 − v 2 − v + 1 The only positive solutions to the equation A 2 ( 1 , w ) = 0 are w = 0 and w = 4 , both of which lead to degenerate triangles A B C . Thus we can assume that v = 1 , and hence that A 3 ( v , w ) = 0 . We can now write A 2 ( v , w ) + ( w + 4 v ) A 3 ( v , w ) = 2 v A 4 ( v , w ) A 4 ( v , w ) = 5 w 2 − 8 ( v + 1 ) w + 4 ( v − 1 ) 2 and we see that A 4 ( v , w ) = 0 . Continuing, we write 2 5 A 3 ( v , w ) + ( 5 w − 7 v − 7 ) A 4 ( v , w ) = A 5 ( v , w ) = ( v 2 + 4 7 v + 1 ) w − 3 ( v − 1 ) 2 ( v + 1 ) and hence deduce that A 5 ( v , w ) = 0 . Since v 2 + 4 7 v + 1 = 0 for positive v , we deduce that w = v 2 + 4 7 v + 1 3 ( v − 1 ) 2 ( v + 1 ) and hence 0 = A 4 ( v , v 2 + 4 7 v + 1 3 ( v − 1 ) 2 ( v + 1 ) ) ( v 2 + 4 7 v + 1 ) 2 = 2 5 ( v − 1 ) 2 ( v 2 − 1 6 v + 1 ) 2 so we deduce that v 2 − 1 6 v + 1 = 0 , so that v = 8 ± 3 7 , and hence w = 6 ± 2 7 . The triple ( 8 − 3 7 , 1 , 6 − 2 7 ) is just a rescaled copy of ( 1 , 8 + 3 7 , 6 + 2 7 ) , so we restrict attention to the case of the triple ( u , v , w ) = ( 1 , 8 + 3 7 , 6 + 2 7 ) .
The smallest angle of this triangle is the angle at the vertex N A . If θ is this angle, then cos θ = 2 ( 6 + 2 7 ) ( 8 + 3 7 ) ( 6 + 2 7 ) + ( 8 + 3 7 ) − 1 = 8 5 + 7 But then sin θ = 8 3 − 7 and hence tan θ = 5 + 7 3 − 7 = 9 1 1 − 4 7 = 3 7 − 2 making the answer 7 + 2 + 3 = 1 2 .
It is worth noting that the next smallest angle of this triangle is the angle at the vertex C , which has cosine 2 8 + 3 7 1 + ( 8 + 3 7 ) − ( 6 + 2 7 ) = 2 ( 1 6 + 6 7 ) 3 + 7 = 2 1 and so the angles of the triangle are θ , 4 1 π and 4 3 π − θ .
Since the pedal triangle of the nine-point centre is degenerate, it follows from the Wallace-Simpson Theorem that the nine-point centre N lies on the circumcircle of A B C .
Note that cos 2 θ = 4 1 ( 1 + 7 ) and sin 2 θ = 4 1 ( 7 − 1 ) , so that cos 2 θ = sin 2 θ + 2 1 . If we set the circumcentre O as the origin, the position vectors of A , B , C all have length R , the circumradius. Since the angle C is 4 1 π , we deduce that ∠ A O B = 2 1 π , so that a ⋅ b = 0 . Similarly we can show that a ⋅ c = − R 2 sin 2 θ and b ⋅ c = R 2 cos 2 θ .
Consider the point X with position vector x = 4 1 ( a + b ) + c = 4 1 ( h + 3 c ) , where h = a + b + c is the position vector of the orthocentre of A B C . Note that X lies on C H , with H X : X C = 3 : 1 . We calculate that ( x − a ) ⋅ ( x − c ) = 1 6 1 ( − 3 a + b + 4 c ) ⋅ ( a + b ) = 4 1 R 2 ( cos 2 θ − sin 2 θ − 2 1 ) = 0 so that X is the position vector of H C , the foot of the altitude from C . Thus the midpoint of H C is the reflection of C in A B , namely the point C ′ . But the nine-point circle passes through the midpoints of A H A , B H B and C H C , so (in particular) passes through the relection point C ′ .
Other points are noteworthy. Again, the fact that C = 4 1 π tells us that the triangle H A H B H C is right-angled, with the right angle at the vertex H C . This means that the nine-point centre (with is the circumcentre of H A H B H C ) is the midpoint of H A H B . Moreover the diameter of the nine-point circle passing through C ′ is perpendicular to the diameter H A H B . We can prove this by calculating the length A H B = A B cos θ , and hence obtaining the position vector of H B as a linear combination of a and c . It is then a matter of calculation to show that c and N H B are perpendicular. The result now follows because O C ′ = n + 2 1 c .