A Tricky Coin
 Zeb's coin box contains 8 fair, standard coins (heads and tails) and 1 coin which has heads on both sides. He selects a coin randomly and flips it 4 times, getting all heads. If he flips this coin again, what is the probability it will be heads? (The answer value will be from 0 to 1, not as a percentage.)
Zeb's coin box contains 8 fair, standard coins (heads and tails) and 1 coin which has heads on both sides. He selects a coin randomly and flips it 4 times, getting all heads. If he flips this coin again, what is the probability it will be heads? (The answer value will be from 0 to 1, not as a percentage.)
The answer is 0.8333.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
No it is just 5/9 = 0.55555. The fact that he already picked 4 heads is IRRELEVANT because it ALREADY HAPPENED with a 100% certainty. The question is really asking "With 8 50% chances and 1 100% chance coins, what is the probability of getting "heads" on this one particular toss?" So the answer should be (50% 8 + 100% 1) / (9 total coins) = 5/9. This whole probability quiz is all screwed up, I don't know who you got to write these questions but they don't know how to word their problems correctly for the answer they want to expect.
Log in to reply
My answer was 5/9 until i saw explanation too , but that would make me answer the following 2 questions as
Q1. Same setting .. He selects a coin randomly and flips it 1 time, getting HEADS. If he flips this coin again, what is the probability it will be heads?
Ans1. The toss is unrelated (it occured with 100% certanity) so : (50%8 + 100%1) / (9 total coins) = 5/9
So far So fine..but
Q2. Again same setting .. He selects a coin randomly and flips it 1 time, getting TAILS. If he flips this coin again, what is the probability it will be heads?
Ans2. The toss is unrelated (it occured with 100% certanity) so : (50%8 + 100%1) / (9 total coins) = 5/9. Well but I knew it was a fair coin since it gave me a tails ... but I will have to ignore it since it was SUPPOSEDLY UNRELATED TOSS
Regards..
Log in to reply
Q3. Again same setting .. He selects a coin randomly and flips it 4 times, getting HEADS. What is the probability he uses the duble head coin?
Ans3. The toss are unrelated 1/9. Same if he had 1,000 flips with head result. And it's 0/9 if he had even one tail result out of 1,000,000 flips.
i thought the same thing until I sat and really thought about it. consider this: your response of 5/9 or .5555 stands true if you picked a random coin from the same above example and flipped the coin only once. Surely the odds must be greater if the coin was flipped 4 times prior and was heads all times. In the same above question it becomes clear if you are told the coin was flipped heads 1000 times prior, what is the probability it would be flipped heads again, it would easily be seen not be .55
You are quite incorrect, sir. The 4 previous heads are irrelevant to the next flip in the sense that they won't affect it. But they are very useful in determining which coin you are holding in your hand.
The 4 heads we observe are not irrelevant. Think about it this way: if you would pick a coin at random and then flipped it 100 times, and all of them came up heads, you'd be pretty certain that this is the unfair coin. So if somebody asked you what is the probability that the next flip of this particular coin was heads, you'd answer something very close to 1.
Same situation here. You are in essence required to answer: what is the probability that I picked the unfair coin given that I have observed 4 heads in a row?
Log in to reply
With apologies, I responded the same without having read your response
I find your question missleading. I calculated it as the probability of getting the dud coin or getting a "proper" coin and then the probability of getting heads (as each through is indipendant of the last) the probability of getting heads with the "proper" coin is (chance of getting the proper coin 8/9 * the chance of getting heads 1/2 ) the chance of getting it multiple times is irrelevant and the chance of getting heads with the dud coin is (chance of getting the dud coin 1/9 * chance of getting heads 1). 8/9 1/2 = 4/9 1/9 1 = 1/9 4/9+1/9 = 5/9 = 0.55555555555...
Log in to reply
The key word that makes your interpretation right is "randomly". I don't think the given answer fits because "randomly" implies to me that the probability of the given coin turning up 4 heads initially is irrelevant to the solution.
Log in to reply
No, it's not irrelevant because he is flipping the same coin, not a new coin every time. If it shows heads four times in a row, it is very probably to be the unfair coin. So the next flip must collect all that higher likelihood to show a head than a tail. Yes, 5/9 (55.55%) is higher than 1/2, but the real probability is much higher than that if you take correctly into account the four heads in a row. My calculation renders 5/6 (83.33%).
Imagine the question this way. If you conduct this exercise, but in 1000 flips your coin has revealed heads in every flip, it is apparent that it is far more likely that you are flipping the unfair coin. In this case, the certainty that you have the unfair coin is near 1, which means you would be very surprised if the 1001st flip was your first tails. This question poses the question when it is more likely that the unfair coin is being flipped, but is less certain.
hi, can you please help me in understanding the question better. I'snt the question same as five tosses and the probability of finding all heads. in which case the probability will be : sum (probablity of choosing 4 fair coins,1 unfair coin * probability of heads) + (probability of choosing 5 fair coins * probabilty of finding heads)
I'm surprised at all the people saying the previous 4 heads is irrelevant... It's totally intuitive that the more times you flip a head, the more likely it is an unfair coin? Maybe the question has been reworded? Haha. Meanwhile, I got it wrong because I didn't think through the whole P(F) • P(H|F) on the bottom and just called that probability 1/16 as well
The key point is that the same coin is flipped 5x. Therefore, each flip is providing information about the coin, and so the answer works out to 5/6 as described. For those who think the answer is 5/9 - that is what it would be if, for each flip, the coin was selected anew from the box -- ie that is what would make the flips independent (which in the problem, they are not).
My answer is 0.1388, if no miscalculation. Coming from 8 (1/32) 1/9+1 1/9. The reasoning I've conducted is the following: if you only had one fair coin the result to get five heads in a row would be 1/32=0.03125. If you now add an unfair coin the result to get five heads in a row chosing randomly a coin would be 1/32 1/2+1*1/2 equal to 0.515; at that step, increasing the number of fair coins in respect with the dud one implies that the probability should decrease. That means the max prob should be 0.515 and the min likelihood 0.03125. In any case I understand the result could never be higher than 0.515, so not 0.833. Thanks for reading me.
Log in to reply
The correct answer is 0.8333. Have you read the other comments in this comments section to try to understand why? Your reasoning is a bit hard to follow because the number expressions you include do not render well. But one crucial mistake I can point out is that you are confusing these two probabilities/events: A) probability of getting five heads in a row, and B) probability of getting heads with one roll, AFTER we have observed 4 rolls that resulted in 4 heads.
I had the same reasoning too but it is wrong unfortunately
i too worked out like @David Moyer
I haven't read the other comments but I want to pose this question. a. If there are 99 fair and 1 unfair coin then given 100 successive head flips what are the odds that a fair coin was selected? b. What is the probability of flipping a head on 101st flip given the above?
Following this logic, P(F | H3) would be 1/2 and P(F | H5) would be 1/5, correct? So could you help me understand why after flipping 5 heads in a row the probability of Zeb having the HH coin is less than after flipping just 2 coins?
Also, why isn't it equal to the probability of flipping 5 heads in a row, which AFAIK is 5/36?
Thank you!
The question is: What is the probability of 5 Heads being flipped given 4 Heads have already been flipped and you started with 8 Fair coins and 1 double headed coin. There are 8 fair coins with a 1/2 probability of Heads, and 1 double headed coin with a probability of heads being 1
Bayes' theorem: P(5H/4H) = P(5H) x [P(4H/5H)/P(4H)].
P5H is the prior probability of 5 heads coming up, which is [(1/2)^5 x 8/9] + 1/9]. The last term, 1/9, is being multiplied by (1)^5 which is 1
P(4H/5H) is probability of the evidence, which is that four consecutive heads have already turned up, so that's equal to 1
P(4H) is the probability of the evidence (4 consecutive heads) without any flipping is [(1/2)^4 x 8/9] + 1/9] where again the 1/9 is multiplied by (1)^4
if you work that out it comes out to 5/6.
I'll be damned I screwed that up forever before figuring it out.
The next flip is independent on the previous flips. The solution should be P ( H ) = P ( H ∣ F ) + P ( H ∣ D ) = 9 8 ⋅ 2 1 + 9 1 ⋅ 1 = 9 5 = 0 . 5 5 6
Log in to reply
The next flip is indeed independent of the previous flips. But you are wrong in your calculations for the probabilities of having a fair coin or having the unfair coin. You assume that the probability of having a fair coin is 8/9, while having the unfair one is 1/9. This is true only as priori probabilities (if we know nothing else). But we have observed the 4 heads in our first 4 flips. This changes the probability of having a fair coin. You are essentially asked to calculate this new probability, and using it you can calculate the probability for the next flip to be heads.
Log in to reply
The prior probability of flipping 5 heads, P(5H), is 8/9 x (1/2)^5 + 1/9. The Probability of the evidence, flipping 4 Heads in a row, is 1 since you have already flipped 4 Heads in a row. However, the prior probability of having flipped 4 Heads in a row is 8/9 x (1/2)^4 + 1/9. Since P(5H/4H) = P(5H) x [(P4H/5H)/P4H], the probability of flipping a 5th Head after 4 have ALREADY been flipped is 5/6.
Log in to reply
@Joe Blow – I think your solution is more illustrative than author of the question's solution could you please solve the last part which is P(5H/4H) = P(5H) X [(P4H/5H)/P4H]. By typing the numbers Thank you.
You can even divide it all by 9. it's the same process I used 😆.
(Trying to avoid relying on Bayes Theorem)
For the first four coin tosses there are 9x16 possible outcomes. (9 for the choice of coin and 16 for the outcome of 4 tosses.) But we can ignore most of these. Only 8 of the outcomes will produce four heads from a fair coin. 16 outcomes will produce four heads from the fake coin. Each of these 24 outcomes is equally likely and hence the probability that Zeb has picked a fair coin is only 8/24 = 1/3.
Now it is simply a matter of calculating the probability of a head as 1/3 x 1/2 plus 2/3 x 1 = 5/6.
8 coins are fair so getting a heads on the 5th toss is 1/2 the 9th coin being double headed gives 1 for getting a head on the 5th toss. This alters the probability of getting heads on the 5th toss from 1/2 to slightly more...… The total possible combinations on the 5th toss is 18 ….. two from each of the nine coins The number of combinations with 5 heads is 10 So P( 5th toss is a head) = 10/18=5/9
There's a 9 8 chance that one of the fair coins is chosen. 9 8 ⋅ ( 2 1 ) 4 = 1 8 1 .
There's a 9 1 chance that the coin with 2 heads is chosen.
The probability that 4 heads is tossed in a row is 1 8 1 + 9 1 = 6 1 .
Given that 4 heads was chosen, the probability that one of the fair coins is chosen is 6 1 1 8 1 = 3 1 .
The probability that the unfair coin was chosen is 6 1 9 1 = 3 2 .
So the probability of the next toss being heads is 3 1 ⋅ 2 1 + 3 2 = 6 5
P(Picked biased | 4 heads in a row) = 4 heads in a row P(4 heads in a row | Picked biased) × P(Picked biased) ( by Bayes’ Theorem ) = 9 8 × ( 2 1 ) 4 + 9 1 1 × 9 1 = 3 2
Picking the biased coin and picking an unbiased coin are exhaustive events since we are given that Zeb picks a coin. ∴ P(Picked unbiased | 4 heads in a row) = 1 − 3 2 = 3 1
P(Next flip is a head | 4 heads in a row) = P(Picked biased | 4 heads in a row) × 1 + P(Picked unbiased | 4 heads in a row) × 2 1 = 3 2 × 1 + 3 1 × 2 1 = 6 5 ≈ 0 . 8 3 3 (3 s.f.)
I am surprised how you got noone's attention so far, yet you presented an effective explanation
P(Real and 4 heads)=8/9 * 1/16 = 1/18 P(Fake and 4 heads) = 1/9 P(Real and 4 heads and then a fifth head) = 8/9 * 1/16 * 1/2 = 1/36 P(Fake and 5 heads) = 1/9
(1/36 + 1/9)/(1/18 + 1/9) = 5/6
I'm not sure if this is a real solution or whether it is just an accident, but that's how I got the answer. I built the entire probability model first and this was what applied to the problem.
He selects a coin randomly and flips it 4 times, getting all heads. If he flips this coin again ...
Is this coin toss about the same coin? ...
If not, each toss should be independent
Log in to reply
«Is this coin toss about the same coin? ... » Answer: yes, it is.
Let f be the number of fair coins.
Let u be the number of unfair coins.
Formula for calculating the probability of Head for any given nth flip would be.
2 × f + u × 2 n f + u × 2 n
So, to answer the original question.
f = 8
u = 1
n = 5
Probability for Head in the fifth flip would be: 2 × 8 + 1 × 2 5 8 + 1 × 2 5
: 6 5
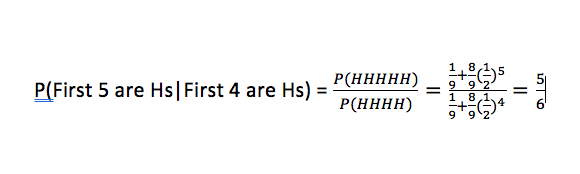
Let F and H 4 be the events of having the fair coin and flipping 4 heads, respectively, and denote the event of having the unfair coin as D .
Via Bayes' Theorem , P ( F ∣ H 4 ) = P ( H 4 ) P ( F ) ⋅ P ( H 4 ∣ F ) = P ( F ) ⋅ P ( H 4 ∣ F ) + P ( F ) ⋅ P ( H 4 ∣ F ) P ( F ) ⋅ P ( H 4 ∣ F ) = 9 8 ⋅ 1 6 1 + 9 1 ⋅ 1 9 8 ⋅ 1 6 1 = 3 1 .
Since there is a 3 1 probability of having chosen the fair coin given that 4 heads were flipped, the probability that the next flip is heads is 3 1 ⋅ P ( H ∣ F ) 2 1 + 3 2 ⋅ P ( H ∣ F ) 1 = 6 5 .