A Unique Set of Cevians (almost)
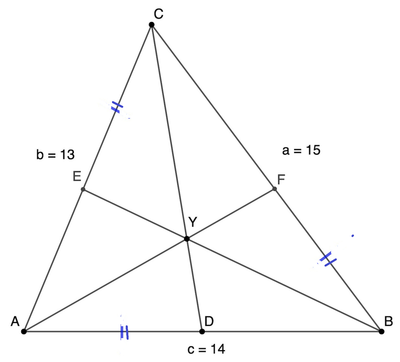
As shown in the figure, △ A B C has side lengths 1 3 , 1 4 and 1 5 , and A D = B F = C E . Find ⌊ 1 0 0 0 0 ⋅ A Y ⌋ .
The answer is 73379.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Thank you for your solution. It's quite clear. I would like to improve my math typesetting skills. Is there a way for me to look at your (or anyone else's) LaTeX code?
Log in to reply
Log in to reply
yes, that's useful, but. I guess this means there is no general mechanism provided by Brilliant?
Just summon me (by tagging me). Like Chew-Seong, I can edit other people's solution as well.
Not to be too persistent, but I ask because someone was apparently able to see my LaTeX here
Log in to reply
I don't understand your question. Care to rephrase this?
Log in to reply
In the solution section of the link I provided, someone (helpfully) corrected by LaTeX by quoting it exactly as I typed it. So I was wondering how that person was able to see my code. Does this make sense?
Log in to reply
Just highlight then paste into a notepad or equivalent, you will get the raw text.
Fletcher, some of us are moderators including Pi Han Goh and I. We can edit the problems and solutions of others.
Log in to reply
Aha. Thank you!
Log in to reply
@Fletcher Mattox – In fact I touched up the figure of this problem. I find that the blue lines for equal lengths were too long. I changed it to equal signs which are easier to understand. I cropped the extra space around to figure. Limit the figure to width=400. Shortened to "Find ⌊ 1 0 0 0 0 ⋅ A Y ⌋ " instead of "Find the length of A Y . Submit ⌊ 1 0 0 0 0 A Y ⌋ . Added ⋅ to avoid people read it as 1 0 0 0 0 × A × Y .
You can leave the substitution of x at the very end. With
A Y A F − 1 = 1 5 x ( 1 4 − x ) ( 1 5 − x ) = 1 5 x 1 ⋅ 1 3 − x x 3 = 1 5 ( 1 3 − x ) x 2
You also wrote A F 2 = 1 3 2 + ( 1 5 − x ) 2 − 2 ( 1 3 ) ( 1 5 − x ) ⋅ = 3 3 / 6 5 cos C . Simplifying this gives A F = ( 5 4 2 − x ) 2 + ( 5 5 6 ) 2
Hence, A Y is equal to 1 5 ( 1 3 − x ) x 2 + 1 ( 5 4 2 − x ) 2 + ( 5 5 6 ) 2 = 3 ( 1 3 − x ) x 2 + 5 ( 4 2 − 5 x ) 2 + 5 6 2
With x ≈ 6 . 9 7 6 , you get the answer.
The cevians are concurrent at Y, the (first) Yff point for △ A B C . They are constructed by marking off a distance x , counter-clockwise from each vertex, where x is the solution to the cubic equation ( a − x ) ( b − x ) ( c − x ) = x 3 . A second Yff point (named for Peter Yff) can be found by measuring clockwise. x is then used to compute trilinear coordinates , α : β : γ for Y .
α = a 1 3 b − x c − x , β = b 1 3 c − x a − x , γ = c 1 3 a − x b − x
Solving the cubic , x ≈ 6 . 9 7 7 6 1 1
And the trilinears are ≈ 0 . 0 7 0 1 6 9 : 0 . 0 8 0 4 1 3 : 0 . 0 6 4 9 1 9
I converted to cartesian coordinates to compute A Y , assigning A = ( 0 , 0 ) , B = ( 1 4 , 0 ) , C = ( 5 , 1 2 ) which results in Y ≈ ( 6 . 3 7 8 7 9 , 3 . 6 2 7 2 7 )
So by Pythagoras, A Y = 6 . 3 7 8 7 9 2 + 3 . 6 2 7 2 7 2 ≈ 7 3 3 7 9 . 8 and 1 0 0 0 0 A Y = 7 3 3 7 9
More information on the Yff triangle here.
Thank you for teaching me something new today.
Log in to reply
You are welcome. I have learned so much from your posts!
Nice problem and solution! I believe your question should say AD = BF = CE (it currently says AD = DB = CE).
Three steps – three theorems: Ceva’s , Stewart’s , Menelaus’s .
Step 1
: to find
x
=
A
D
=
B
F
=
C
E
By Ceva’s theorem on
△
A
B
C
we have
D
B
A
D
⋅
F
C
B
F
⋅
E
A
C
E
=
1
⇒
1
4
−
x
x
⋅
1
5
−
x
x
⋅
1
3
−
x
x
=
1
⇒
x
3
=
(
1
3
−
x
)
(
1
4
−
x
)
(
1
5
−
x
)
⇒
2
x
3
−
4
2
x
2
+
5
8
7
x
−
2
7
3
0
=
0
which solves to
x
=
7
+
3
3
6
3
−
6
3
+
1
5
0
9
2
6
5
1
1
−
3
6
(
−
6
3
+
1
5
0
9
2
6
5
1
1
)
2
9
3
⇒
x
≈
6
.9761093080953896
Step 2
: to express
A
F
in terms of
x
By Stewart’s theorem on
△
A
B
C
we have
A
F
2
=
B
F
+
F
C
A
C
2
⋅
B
F
+
A
B
2
⋅
F
C
−
B
F
⋅
F
C
=
1
5
1
3
2
⋅
x
+
1
4
2
⋅
(
1
5
−
x
)
−
x
⋅
(
1
5
−
x
)
=
x
2
−
5
8
4
x
+
1
9
6
Thus,
A
F
=
x
2
−
5
8
4
x
+
1
9
6
Step 3
: to find
A
Y
By Menelaus’s theorem on
△
A
B
C
intersected by a line at points
Y
,
C
and
D
we have
Y
F
A
Y
⋅
C
B
F
C
⋅
D
A
B
D
=
1
⇒
Y
F
A
Y
=
F
C
C
B
⋅
D
A
D
A
⇒
Y
F
A
Y
=
(
1
5
−
x
)
(
1
4
−
x
)
1
5
x
⇒
Y
F
A
Y
=
x
2
1
5
(
1
3
−
x
)
from the equation in step 1
⇒
A
Y
=
x
2
1
5
(
1
3
−
x
)
(
A
F
−
A
Y
)
⇒
A
Y
⋅
(
1
+
x
2
1
5
(
1
3
−
x
)
)
=
x
2
1
5
(
1
3
−
x
)
⋅
x
2
−
5
8
4
x
+
1
9
6
⇒
A
Y
=
x
2
−
1
5
x
+
1
9
5
3
5
(
1
3
−
x
)
5
x
2
−
8
4
x
+
9
8
0
Substituting the value of x we found in step 1 we get A Y ≈ 7 . 3 3 7 9 8 4 5 7 0 6 2 4 6 3 4 6 8 .
For the answer, ⌊ 1 0 0 0 0 ⋅ A Y ⌋ = 7 3 3 7 9 .
Nicely organised. You should teach this stuff!

Let A D = D B = C E = x . By generalized angle bisector theorem , we have:
A D B D x 1 4 − x ⟹ sin ∠ A C D sin ∠ B C D = C A ⋅ sin ∠ A C D B C ⋅ sin ∠ B C D = 1 3 sin ∠ A C D 1 5 sin ∠ B C D = 1 5 x 1 3 ( 1 4 − x )
Similarly,
A F Y F A Y A F − A Y A Y A F − 1 ⟹ A Y = C A ⋅ sin ∠ A C D C F ⋅ sin ∠ B C D = 1 3 ⋅ 1 5 x ( 1 5 − x ) ⋅ 1 3 ( 1 4 − x ) = 1 5 x ( 1 4 − x ) ( 1 5 − x ) = ( 1 4 − x ) ( 1 5 − x ) + 1 5 x 1 5 x ⋅ A F
We need to find A F and x to find A Y . To find A F , we need to first find x and we can use Ceva's theorem as follows.
E A C E ⋅ D B A D ⋅ F C B F 1 3 − x x ⋅ 1 4 − x x ⋅ 1 5 − x x x 3 − ( 1 3 − x ) ( 1 4 − x ) ( 1 5 − x ) ⟹ x = 1 = 1 = 0 ≈ 6 . 9 7 6 1 0 9 3 0 8
To find A F , we use cosine rule . First 1 4 2 = 1 3 2 + 1 5 2 − 2 ( 1 3 ) ( 1 5 ) cos C ⟹ cos C = 2 ( 1 3 ) ( 1 5 ) 1 3 2 + 1 5 2 − 1 4 2 = 6 5 3 3 and
A F 2 ⟹ A F = 1 3 2 + ( 1 5 − x ) 2 − 2 ( 1 3 ) ( 1 5 − x ) cos C ≈ 1 2 7 . 4 6 7 4 6 4 7 ≈ 1 1 . 2 9 0 1 4 9 0 1
Therefore, A Y = ( 1 4 − x ) ( 1 5 − x ) + 1 5 x 1 5 x ⋅ A F ≈ 7 . 3 3 7 9 8 4 5 7 1 ⟹ ⌊ 1 0 0 0 0 ⋅ A Y ⌋ = 7 3 3 7 9 .