Particle Flying Through A Ramp
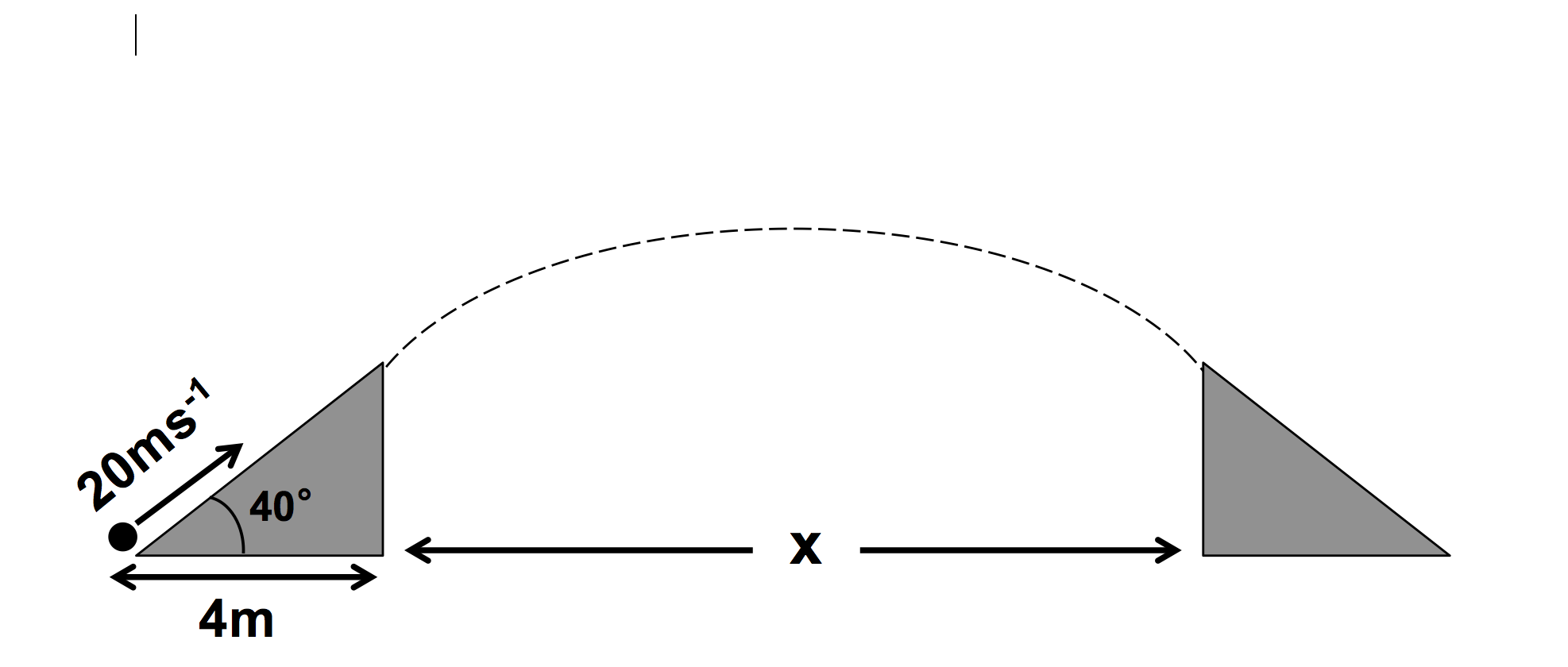
A particle of mass 1 kg , is projected with speed 2 0 m/s , over a ramp set at 4 0 ∘ to the horizontal. The length of the ramp is 4 m , and the coefficient of friction between the particle and ramp is 0.8. The particle lands perfectly on another identical ramp x metres away. Assuming g = 1 0 m/s 2 , what is x to 2 decimal places?
The answer is 26.47.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Brilliant and a very detailed solution!
We can use energy method also as follows.
E
n
e
r
g
y
l
e
f
t
f
o
r
f
l
y
−
o
v
e
r
=
K
E
−
P
E
−
f
r
i
c
t
i
o
n
w
o
r
k
=
2
1
∗
1
∗
2
0
2
−
1
∗
1
0
∗
4
T
a
n
4
0
−
.
8
∗
1
∗
1
0
∗
4
=
2
1
∗
1
∗
v
2
,
v
=
v
e
l
o
c
i
t
y
l
e
f
t
t
o
\
f
l
y
.
∴
x
=
r
a
n
g
e
=
1
0
2
(
2
1
∗
1
∗
2
0
2
−
1
∗
1
0
∗
4
T
a
n
4
0
−
.
8
∗
1
∗
1
0
∗
4
)
∗
S
i
n
8
0
=
2
6
.
4
7
8
7
.
First, find the deceleration as the particle moves along the ramp..
Flim
=
u
R
=
0
.
8
⋅
1
0
⋅
cos
(
4
0
∘
)
=
8
cos
4
0
∘
Horizontal Component of weight is
1
0
sin
(
4
0
∘
)
Therefore..
a
=
−
1
8
cos
4
0
∘
+
1
0
sin
4
0
∘
=
−
(
8
cos
4
0
∘
+
1
0
sin
4
0
∘
)
From here we can simply use
SUVAT
equations..
u
=
2
0
m/s
,
v
=
?
,
s
=
cos
4
0
∘
4
,
a
=
−
(
8
cos
4
0
∘
+
1
0
sin
4
0
∘
)
v=\sqrt{20^{2}+(2\cdot-(8\cos40^\circ+10\sin40^\circ)\cdot \frac{4}{\cos40^\circ}
v = 1 6 . 4 0 m/s (by the top of the ramp)
Now it's a normal projectile question:
u
=
1
6
.
4
0
sin
4
0
∘
,
v
=
0
,
t
=
?
,
a
=
−
1
0
t
=
−
1
0
−
1
6
.
4
0
sin
4
0
∘
=
1
.
0
5
4
seconds for half the time
Therefore total time is
1
.
0
5
4
×
2
=
2
.
1
0
8
s
=
x
=
u
t
x
=
1
6
.
4
0
cos
(
4
0
∘
)
⋅
2
.
1
0
8
x
=
2
6
.
4
7
The actual answer comes out to be 26.47 which is nearer to 26 than 27. I dont get that if the answer is decimal, why does the author ask for an integer without any specifications...?
Log in to reply
Due to the large amount of trig involved there is a large area for error in rounding, I asked for it in integer form as I was hoping this error would be lost through doing this.
Log in to reply
You kinda created an error, instead of removing it. You should have asked about something more appropriate like the floor function or the ceiling function.
Log in to reply
@A Former Brilliant Member – Thanks. Those who answered 26 have been marked correct.
I have updated the answer to 26.47.
The forces acting on the body is given in the free body diagram.
f k represents the kinetic frictional force acting on the body.
Now, The net acceleration of the body,
a = − [ m g sin 4 0 0 + μ k N ] , where μ k is the coefficient of kinetic friction.
Let v be the velocity of particle at B and u be the velocity of particle at A ,
Now, using Newton's equations,
v 2 = u 2 + 2 a s , where s is the distance between A and B .
⇒ v 2 = u 2 − 2 [ m g sin 4 0 0 + μ k N ] s Substituting values,
⇒ v 2 = 2 0 2 − 2 . [ 1 × 1 0 sin 4 0 0 + 0 . 8 × 1 × 1 0 × cos 4 0 0 ] . cos 4 0 0 4 = 2 6 8 . 8 7 2 0 2 9 m / s
{Note: N = m g cos 4 0 0 }
At B , the body leaves the ramp and undergo projectile motion. The body will be projected at an angle 4 0 0 with the horizontal.
Since both both ramps are at same level, the projectile lands perfectly on other ramp when the range of projectile is maximum.
Now we could use the equation for range of projectile,
R = g ( u 1 ) 2 s i n 2 θ , where
u 1 ⟶ Velocity with which the projectile is projected
θ ⟶ Angle made by projectile with horizontal at time of projection.
Now we have ( u 1 ) 2 = v 2 = 2 6 8 . 8 7 2 0 2 9 m / s and θ = 4 0 0
∴ x = R = 1 0 2 6 8 . 8 7 2 0 2 9 × s i n 8 0 0 = 2 6 . 4 7 8 7 m
PS: If you have doubt about how the equation of "Range of projectile" came through, let me know. I'll give the explanation.