AB Split
Cutting only along the grid lines, we can divide this figure into two congruent parts such that all the As are in one part and all the Bs are in the other.
Will the star end up with the As or Bs?
Note: "Congruent" means "of the same shape and size".
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
I still don't get it
Log in to reply
Could you be more specific? (To be honest, the answer is overkill for practical circumstance, I was just trying to show the steps can be logical - if you can get that the left must all be As and the right must be all Bs, then play around enough to realize the pieces must be 180 degrees rotations of each other, the rest can be worked out brute force.)
Log in to reply
After the fillings of the two opposing vertical collumns, I didn't understand the eliminating of the symmetries.
Log in to reply
@Giovanna Andrade – Take the B in row 4, column 2. We know the corresponding A is a 180 degree rotation. So we rotate 180 degrees and find the position at row 2, column 5, and put an A at it.
Log in to reply
@Jason Dyer
–
I get that,I get that the 180 degrees works. What I don't get is the fourth and fifth grids with those red spots eliminating the symmetries that are not the 180 degrees rotation, this one part: "There isn't enough room on the grid for the congruent parts to be made by translation, so we'd like to think about what sort of symmetry relates the two congruent parts. It can't be a horizontal reflection or diagonal reflection, as shown:
[4th grid] [5th grid]
Can't be horizontal reflection Can't be horizontal reflection
90 degree rotations also are quickly eliminated in a similar fashion."
I should've been more clear, sorry.
Log in to reply
@Giovanna Andrade – In the horizontal, you can't connect A to the As or B to the Bs without the paths crossing.
In the diagonal reflection, the Bs would need another B overlapping a space that already has an A to match the picture of As already drawn.
Log in to reply
@Jason Dyer – Alright, I understood it. Thank you!!
Just one more, if you will: I was just wondering if the diagonal reflection wouldn't be just a special case of the 180 degrees rotation for a rectangle like this, and in that case we could dismiss it, is that true? if it isn't what would be a case where the diagonal reflection works and the 180 rotation don't for this grid?
Log in to reply
@Giovanna Andrade – You're on the right track - you could eliminate the diagonal for a couple reasons based on the shape of the grid. This isn't true for every single puzzle of this type, and I was trying to give a "general approach". (For an example, try drawing an asymmetrical triangular piece, then make a diagonal reflection and draw that. You'll get a figure other than the rectangle given, but you'll also get a situation where you can reflect but not rotate 180 degrees to get the match.)
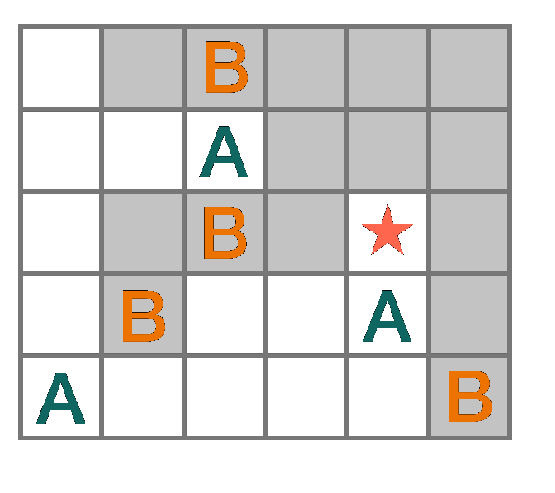
Look at the next standard answer, by David Vreken, & notice that if you print that image and cut out the single strip of blue boxes (which happen to contain all of the As and the star) you can swing it around to exactly cover (=congruent) the complementary (all of the rest of the boxes in the original 5x6 rectangle) strip of white boxes containing all of the Bs.
I did not understand that I was supposed to add A's and B's to fill the square. I thought I was supposed to cut the square in such a way that the two pieces were congruent, and one piece had only A's and the other piece had only B's. And I was to say which of the two congruent pieces had the star.
Log in to reply
Indeed, if you now use the picture shown as a pattern, you can cut to get the two congruent pieces. It's just a more convenient way to notate by filling in the squares. (Note this notation method fails if you're allowed arbitrary cuts not just on the grid lines - we had a puzzle like that a few months ago.)
You don't have to put in those As & Bs, that is just to indicate where to cut: to separate the As from the Bs.
How was I supposed to get from this problem description that the parts were attached?
Log in to reply
It does say, "divide this figure into two congruent parts". if there are more than 2 parts; A & B, then that requirement is not met. My solution for answer "B" depends on his accepting that a single point can act as an isthmus between continents of As or of Bs. IE: https://drive.google.com/file/d/1IihsHbzqXklKBwvZ6g_61QY5uPYswBxD
It can't also be A, because that would cut off the B in the top row. Therefore it must be B.
Could you explain why this is the case. I do not see why we can tell what the cutting cannot seperate this point from the B's
Log in to reply
Oh, you could choose to cut off the B on the bottom instead. I rephrased to be clear about this.
Since lines intersect at a point, does a point join or separate opposite quadrants? If the answer is arbitrary, I have drawn a cut-line similar to [Aaa -Laura GaoGao], that shows perfectly congruent shapes that put the star in B (as implied by your color usage). I cannot seem to paste the image here, so here is a cryptic link to the image. https://drive.google.com/file/d/1IihsHbzqXklKBwvZ6g_61QY5uPYswBxD/view?usp=sharing (Note that the line connecting the two big pieces of As (same for Bs) consists of a single point isthmus, indicated imprecisely by the hand drawn line. I have not looked into the hairball of additional solutions this might generate.
I understand that it can't be diagonal reflection because it would necessitate overlapping sections, but I can't figure out what the diagram for the diagonal case is indicating. Would you mind explaining what the arrows mean in that case?
Log in to reply
For the B to match the A piece, it would have to overlap where there is already some A. (The two arrows are on identical spots, if you are using that particular transformation).
Here is one way to split the figure into two congruent parts:
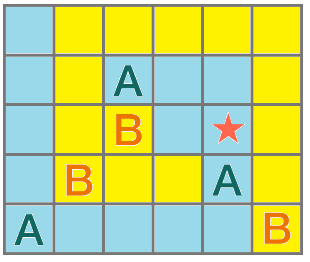
The star ends up with the As.
This is what I found as the solution
What if instead of coloring the Star square blue, you color in blue the square left of the rightmost A?
I believe that this is not only one way, but in fact the only way.
This is one way to cut the grid, but is this the only way?
Log in to reply
Since the question lacks a "not enough information" option, we can deduce that finding one way to cut the grid is sufficient. That is, either there is no other way to cut the grid, or any other ways to cut the grid also put the star in the A group.
I don't understand why this is not a valid cut.

Have I misunderstood the problem statement?
Moderator note:
As explained in the comments, the pieces need to be "congruent" (the same size and shape).
The key word is "congruent" which means that the two parts must be the same size and shape (albeit reflected or rotated).
Log in to reply
I didn't know that, thanks for taking the time to explain.
Not congruent
It would be nice if someone could make a note in the problem clarifying the meaning of congruent, as it can be confusing
Hmm, but I think congruent exactly means CONGRUENT, not SIMILAR. It means that the shapes shall be same, not just the no of boxes.
I initially had the same idea- I thought only the area had to be congruent
Congruent in this case means the black area needs to be the same shape and size (count of boxes), but (not necesarily the same orientation) as the red area.
Is there a better way to phrase this problem?, it doesn't really click.
The incongruency is that you have a row of B across the top, so you need a row of A across the bottom, although to be fair (but not quite satisfying the requirements), you could make a perfectly symmetrical cut if you made one additional cut across the bottom of the bottom right five boxes! (without the shown cuts on the left and bottom!) ... Because I discarded this option, I have another tricky cutline-based answer.
Those regions do not have equal areas. The areas are 12 and 18 instead of 15 and 15. Congruence implies equal areas.
I had to Google 'congruent' 😂😂
Can't it be in the B's with something like this?
oops never mind I didn't see the "congruent" part
This is actually close to one of my answers that chooses 'B', if I can figure out how to insert a picture of my solution.
Log in to reply
how to insert a picture:
https://lh3.googleusercontent.com/-QyoWxIoCHNs/Wr2FnwD8rsI/AAAAAAAAAgg/Az6FcMRoWlYvwBy_pahIx5Cy7iBQtNVwACL0BGAYYCw/h800/2018-03-29.png

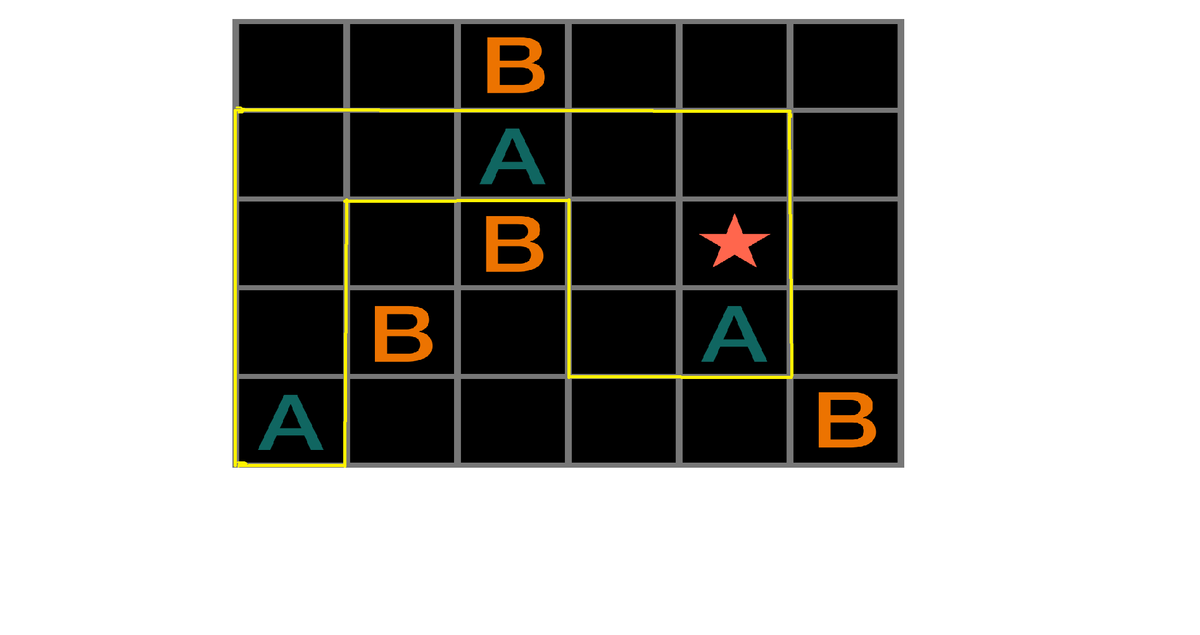
First consider the corner opposite to A.
It can't also be A, because if it is connected with the As on the left it would cut off at least one B from the remaining Bs. Therefore it must be B.
Additionally, if B was in the upper left corner, then there wouldn't be enough room to form a congruent shape of As in the remaining part of rectangle. So A must be the upper left corner.
Therefore, the far left must then be all As and the far right must be all Bs (otherwise, again, there will be a portion of one letter "cut off" from another). This leads to filling in the grid as shown:
There isn't enough room on the grid for the congruent parts to be made by translation, so we'd like to think about what sort of symmetry relates the two congruent parts. It can't be a horizontal reflection or diagonal reflection, as shown:
90 degree rotations also are quickly eliminated in a similar fashion.
Therefore, the two parts must be related by a 180 degree rotation. Knowing this, we can rotate the known squares by 180 degrees and fill in their opposites (that is, we take a given A square, rotate it 180 degrees on the grid, and fill it in with B; we take any Bs and fill in their corresponding rotated squares with As).
With these squares filled in, the remainder of the connections to make two congruent parts are forced.