Accelerated Mirrors!

Classical Mechanics Level 2

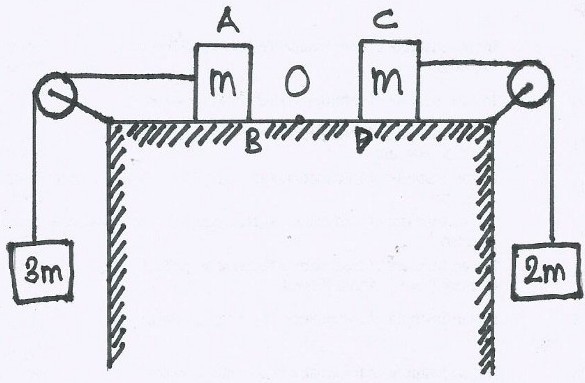
Two blocks each of mass $m$ lie on a smooth table. They are attached to two other masses as shown in the figure. The pulleys and strings are light. An object O is kept at rest on the table. The sides AB & CD of the two blocks are made reflecting. The acceleration of two images formed (of the object O) in those two reflecting surfaces with respect to each other is :

\frac{g}{3}

\frac{5g}{3}

\frac{17g}{6}

\frac{5g}{6}

1 solution

Plinio Sd
Jul 17, 2015

Using the second Newton's law, $F=ma$ , we can find that the acceleration of the right-side system is given by $2mg = (m+2m)a_R \Rightarrow a_R = \dfrac{2g}{3}.$ Analogously, for the left-side system, we find $a_L = \dfrac{3g}{4}$ . Note that when an image is reflected, if the distance between the mirror and the object is $\Delta s$ , then the distance between the reflected image and the object is $2\Delta s$ , which implies that the acceleration is multiplied by $2$ too. Then, the two reflected images separates themselves with an acceleration of $2 a_R + 2 a_L = \boxed{ \dfrac{17g}{6} }.$

Could you please explain in brief why you multiplied your answer by 2.
Thanks!

Akhil Bansal - 5 years, 9 months ago

If the distance between a plane mirror and an object is given by $\Delta s(t)$ , then the distance between the object and its reflexion is given by $2\Delta s(t)$ . Using this, we know that the distance between the reflected images will be $2\Delta s_R(t) +2\Delta s_L(t)$ . As we know that the acceleration is the second derivative of space in respect to time, then $\begin{aligned} a(t) &= \frac{d^2}{dt^2} [2\Delta s_R(t) +2\Delta s_L(t)] \\ &= 2 \frac{d^2}{dt^2}\Delta s_R(t) + 2 \frac{d^2}{dt^2} \Delta s_L(t) \\ &= 2 a_R(t) + 2 a_L(t). \end{aligned}$ .

Plinio SD - 5 years, 7 months ago

I still don't understood....😥😥

Abhimanyu Gehlot - 3 years, 4 months ago

@Abhimanyu Gehlot – Which part you didn't understand? Did you understand why the distance is doubled?

Plinio SD - 3 years, 4 months ago

@Plinio Sd – So relieved! My book did not multiply by 2 and gave the final answer as 17g/12. I was so worried. Huh!

Ujjwal Rawat - 3 years, 4 months ago

Listen the distance of object form mirror is x then its Image distance form mirror is also x so the distance btwn Image and object is 2x

Ankit Mishra - 1 year, 11 months ago

So if distance is increasing by 2 acceleration should also increase by two

Ankit Mishra - 1 year, 11 months ago

Accelerated Mirrors!

1 solution

0 pending reports