Accelerating train

Constant acceleration means that speed increments by the same amount per unit time. Because it is accelerating, it takes the train more time to pass the pole between the front and the middle than between the middle and the end. Therefore, more time spent means the speed increase must be greater, and so when the middle of the train passes the pole it must be moving faster than 60 km/h

If the train's acceleration is $a$ , and the train's length is $2s$ , and if its speed at the half-way mark is $v$ , then $80^2 - 40^2 \; = \; 2a \times 2s \; = \; 4as \hspace{2cm} v^2 - 40^2 \; = \; 2a \times s \; = \; 2as$ so that $80^2 - 40^2 = 2(v^2 - 40^2)$ , and hence $v^2 = \tfrac12(80^2 + 40^2) = 4000$ , so that $v = 20\sqrt{10} > 60$ . Note that we are using kilometres as the unit of distance, and hours as the unit of time.

Constant acceleration means the amount of energy used to make the train go faster is the same the whole time the train is speeding up. However we know that resistance becomes higher (from wind and wheels against the track) at higher speeds. So the train must be going faster than 60 km/h at the halfway point to be able to reach 80 km/h in the the remainder of the time.

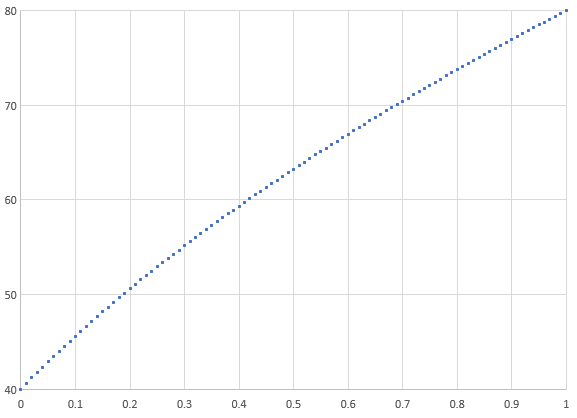
Here is a solution which is not original.

Because the train is accelerating constantly, it must be under the action of constant force. But this means the work done by the train grows in proportion with the distance traveled, since it is simply the product of the force applied with the distance. This work is converted to kinetic energy. So, that means the kinetic energy halfway through is exactly halfway between the initial and final kinetic energies.

Cancelling masses on both sides, we have $v= \sqrt{\frac{1}{2}(40^2 + 80^2)}$ , which by power mean inequality , is larger than 60.

In the accelerated train, the speed at middle point is given by

√[(u^2+v^2)/2] > [(u+v)/2]

i.e. 63.245 > 60.0

Where u=40.0 and v=80.0 are initial and final speeds, respectively.

it's just a trick question relying on people to confuse velocity and acceleration. we don't really know what speed is or how a 'filmstrip' view of relativistic objects works, only that it more or less works in our day to day reality.

Since the question isn't strictly asking for a specific speed ( only a comparison to the average speed ), we don't need to calculate.

Over the first half of the journey the train will experience an acceleration over some time $t$ and will achieve a change in velocity of $\Delta v$ . Over the second half of the journey, the train will accelerate over some time less than $t$ because of:

1) It has a higher average velocity than the first leg

2) traveling over the same distance.

Thus, the train will experience a change in velocity of $\Delta v - \epsilon$ over the second half of the journey. Adding up the total change in velocity to the initail velocity and equating it to the final velocity we have:

$\displaystyle v_o + \Delta v + ( \Delta v - \epsilon ) = v_f$

Where,

$\displaystyle \Delta v = v_{\frac{L}{2}} - v_o$

$\displaystyle v_o + (v_{\frac{L}{2}} - v_o) + (v_{\frac{L}{2}} - v_o - \epsilon) = v_f$

Combining like terms and solving for $v_{\frac{L}{2}}$ ( absorbing the factor of 1/2 into $\epsilon$ in the second term fro simplicity )

$\displaystyle v_{\frac{L}{2}} = \frac{v_f + v_o}{2} + \epsilon$

The first term is the average velocity, and we can see the speed of the train at position $\frac{L}{2}$ is greater than it by some amount $\epsilon > 0$

Let length of train be 2l. Let midpoint of train passes by speed v. Then,applying equations of motion , v^2-40^2=2al(for first half) And 80^2-v^2=2al(2nd half) So, 2v^2=6400+1600 V^2=4000 V=20√10. -Biswaranjan