Acceleration With Constraint
A block of mass m can slide freely in a slot made in a bigger block of mass M , as shown in the diagram above. There is no friction anywhere in the system.
The block m is connected to one end of a string whose other end is fixed at point P . The system is released from rest when the string at P makes an angle θ with horizontal.
What is the acceleration of the smaller block with respect to the bigger block, as soon as the system is released?
Details and Assumptions:
- m = 3 1 kg
- M = 2 1 kg
- θ = 4 5 ∘
- g = 1 0 ms − 2
The answer is 1.666.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Is there a way to intuitively explain why the projection of l onto x is wrong? Must it be concluded from calculations alone?
Log in to reply
I would try to nail down what is being projected onto what. What ground is there for projecting ℓ onto x ? How about the other way around?
When you differentiate x 2 + H 2 = l 2 , may you explain to me where H goes? What were you differentiating with respect to?
Log in to reply
It is differentiated wrt time... So H is constant wrt to time
Log in to reply
How do you know H is constant wrt time? (When they are falling, wouldn't H increase...?)
Log in to reply
@John Frank – No, the vertical distance between the bigger block and the point P is 'H'. You see, the dimensions of bigger block aren't changing wrt time, so the H remains same
Log in to reply
@Sparsh Sarode – @Sparsh Sarode explained it well. The height of the block below the ceiling isn't changing so H ˙ = 0 .
To solve the problem, I considered the energy over a short time interval d t . I believe it is simpler than the other solutions, because it bypasses the equations of general motion.
Let a v and a h be the vertical and horizontal accelerations respectively. (Only m moves vertically, while both m and M move together horizontally, so there is no ambiguity.) The relative acceleration, which is what we are asked for, is simply a v .
I will not go into detail about this part, but by analyzing the forces on the two bodies we arrive at the following equations (where T is tension).
m a v = m g − T
( m + M ) a h = T cos θ
Which combine (by eliminating the unknown tension) to give ( m + M ) a h = m ( g − a v ) cos θ .
To solve the problem, we still must find another relationship between a h and a v . To do this I used conservation of energy.
In the limit of short time intervals, the acceleration approaches linearity (in exactly the same way that curves become straight lines when looking at smaller domain-intervals). This means that if we take an infinitesimal time interval to have occurred, we can treat the accelerations a v and a h as constants.
The idea is, as usual, that the potential energy released in this time interval d t (from m moving with gravity) is equal to the kinetic energy gained (through acceleration). If a h is constant over d t , then the vertical height that m moves down will be 0 . 5 a h ( d t ) 2 which makes the energy equation:
0 . 5 m g a h ( d t ) 2 = 0 . 5 m ( a v d t ) 2 + 0 . 5 ( m + M ) ( a h d t ) 2
Now we see, as we might have hoped, that the d t 2 factor cancels from both sides. We are left with the other relationship between a v and a h which we needed. (Two unknowns, a v and a h , require two (non-redundant) equations to be determined.) The problem is essentially solved, all that is left is to eliminate a h and simplify the resulting quadratic. The quadratic has two solutions, one of which leads to the answer. The other solution is a v = g , which represents the same situation but without the rope.
So you see, we do not need to delve into the general motion and then use the initial conditions in order to solve the problem. There is nothing wrong with that approach, it's just that it can be more difficult to do it that way in other problems.
Let the acceleration of M1 be ' a 1 ' ms^-2 towards left,in a frame coinciding with m 1
l 2 = x 2 + y 2
where l is the length of the string above m 1 ,and x the horizontal distance between the moving pulley and m 1 ,
l ′ 2 +l(l")= x ′ 2 +x(x")
At the initial moment both l' and x' are zero,so l(l")=x(x") l"=cos€*x" By definition,l"=a2,€=45° and x"=a
So a 2 = a 1 c o s 4 5 °
Tcos45°=(m1+m2)a1
m2g-T=(m2)(a1cos45°)
a1=(m2gcos45°)/(m1+m2(1+(cos45°)^2)) Now the magnitude of acceleration of m2 is
a1√(1+(cos45°)^2) Now a1=√2 m2g/(2m1+3m2) So a=√3 m2g/(2m1+3m2) So 3a comes to be 3√3*m2g/(2m1+3m2) m1=0.5kg and m2=(1/3)kg
So,3a=(√3g/2)=(5√3)ms^-2 So since the expected ans is a number,could you explicitly state whether you were asking for absolute acceleration of m or only vertical acceleration
If you are asking for only relative acceleration of m2 at the initial moment then
a=a1cos45°
Now a1=(5√2/3) So a1cos45°=5/3,therefore 3a=5ms^-2,which is the expected ans,so you have to ask for relative acceleration which is vertical of m2 at the initial moment,if you are expecting above ans,if you ask for absolute it is the one which I earlier enumerated Thanks for bearing with unformatted comment
A bigger thanks to you @Sparsh Sarode for bearing with my horrible looking,non-latex comment,hope I made my point clear though,you have actually asked for relative acceleration😀
Log in to reply
Yea.. I have changed the question.. :)
Log in to reply
congrats ...another good ques ! can u post some more like this (or even tougher??) ,i'll be glad if u did that ! @Sparsh Sarode
Log in to reply
@A Former Brilliant Member – K.. I will surely post one... :) thx..
The question clearly states tht the acceleration is wrt ground(absolute acclerarion).. Due to time constraints I ain't finding time to post solution.. I am working on it.. Shortly I will post the solution.. U can see it for urself what went wrong
Please use Latex to post the solutions.
I think Chirag is correct ans is 5 relative to bigger block
I am sorry.. It should be wrt bigger block.. Thanks for pointing out
First, we label the diagram with some variables to describe the various quantities.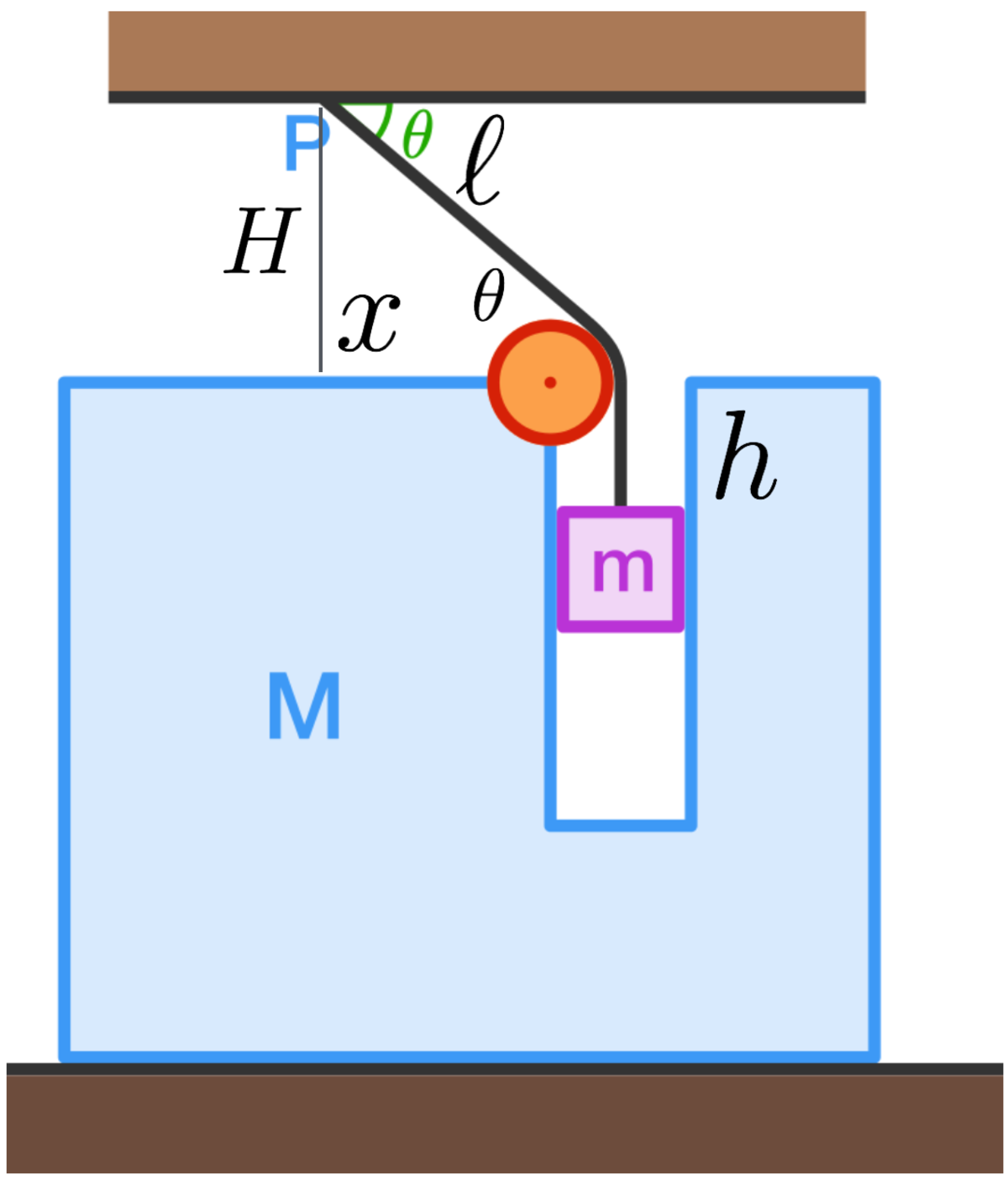 ℓ
and
h
describe the length of wire above and below the pulley, respectively.
H
is the distance from the top of
M
to the ceiling.
x
describes the horizontal position of
M
relative to the gray line through the point
P
.
ℓ
and
h
describe the length of wire above and below the pulley, respectively.
H
is the distance from the top of
M
to the ceiling.
x
describes the horizontal position of
M
relative to the gray line through the point
P
.
Notice that m and M move with the same acceleration toward the left, so the relative acceleration between m and M is given by m 's vertical motion.
The force on m in the y ^ -direction is a contest between the pull of gravity, and the tension from the wire T , so that the vertical motion of m is given by m h ¨ = T − m g . As M and m move together toward the left, the equation of motion in the x ^ -direction is given by ( M + m ) x ¨ = T cos θ . Now, we have two equations in three unknowns ( T , x , and h ). First, notice that ℓ + h = const. , and so h ¨ = − ℓ ¨ .
We can also establish a constraint between ℓ and x via the right triangle between ℓ , H , and x : ℓ 2 = x 2 + H 2 . Taking derivatives, we have ℓ ˙ 2 + ℓ ℓ ¨ = x ˙ 2 + x x ¨ . As we're interested in the initial motion, we have ℓ ˙ = x ˙ = 0 and thus ℓ ¨ = x ¨ ℓ x = x ¨ cos θ . Note that this is different from what might feel natural, an erroneous projection of ℓ ¨ onto x ¨ , which would yield ℓ ¨ cos θ = x ¨ .
Making the replacements in the second equation above, we have m h ¨ = m g − T . Dividing the second through by cos θ , we have cos 2 θ m + M h ¨ = T .
Adding the equations together, we eliminate T and isolate h ¨ to find a = m + cos 2 θ m + M m g . Plugging in the values for m , M , and θ , we find h ¨ = 3 5 m / s 2 .