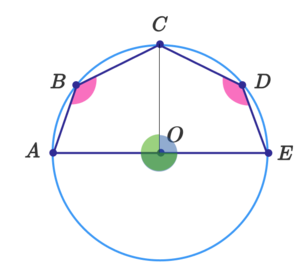
Sum of Opposite Angles

Relevant wiki: Cyclic Quadrilaterals

Join $BE.\angle ABE =90^\circ$ since angle subtended by a semicircle is always a right angle.
Let $\angle CBE=x.$ So, $\angle CDE=180-x$ since $CBED$ is a cyclic quadrilateral .
Therefore $\angle ABC+\angle CDE=90+x+180-x=\boxed{270}.$

Here's the solution that was hinted at by Chung Kevin's comment of "Relate $\angle ABC$ to $\angle AOC$ .".

Since angle at center is twice angle at circumference, $2 \times \angle ABC = \angle AOC$ . However, note that we're taking the reflex angle.

Similarly, $2 \times \angle CDE = \angle COE$ , where we're measuring the reflex angle.

If we sum $\angle AOC + \angle COE$ , it is tempting to conclude that we get $\angle AOE = 180 ^ \circ$ . However, we have to bear in mind what values we're summing. If you look at the image on the right, it's clear that the sum should instead be $540 ^ \circ$ .

Hence, $\angle ABC + \angle CDE = \frac{ 540 ^ \circ } { 2} = 270 ^ \circ$ .

When two chords intersect on the circumference and subtend an arc, the angle formed is half of the angle formed by the two radii that subtend the same arc.

Since the figure is half an octagon, the two radii are $OC$ and $OE$ , so the angle of the arc is $270^{\circ}$ and this makes each of the marked angles is $135^{\circ}$ . Their sum is $\boxed{270^{\circ}}$

Figure is 1/2 an octagon. Angles at center of an octagon (<AOB,<BOC, etc) are 45° (360°/8). Triangles formed with the origin are Isosceles with a 45° and two 67.5° angles [(180°- 45°)/2]. Angles ABC and CDE each contain two 67.5° angles, equaling 135°, times two = 270°

Chords above the diameter and their reflections below the diameter form a regular octagon.

∠ABC and ∠CDE intercept 3/4 of the circumference to form arcs of 3/4 * 360° = 270°

Each inscribed angle of a circle is measured by 1/2 its intercepted arc.

∠ABC = ∠CDE = 1/2 * 270° = 135°

∠ABC + ∠CDE = 270°