Adding Powers of 9
9 0 + 9 1 9 1 + 9 2 9 2 + 9 3 = = = 1 + 9 9 + 8 1 8 1 + 7 2 9 = = = 1 0 9 0 8 1 0
Is the following true for any positive integer n ? 9 n + 9 n + 1 = 9 n × 1 0
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
16 solutions
Moderator note:
Since some comments asked for more detail:
At the first line, 9 n is written as 9 n × 1 (this makes the factoring on the next line easier to see).
Also on the first line, 9 n + 1 is the same thing as 9 n × 9 . If you're having trouble seeing this, consider the meaning of 9 n + 1 : you have 9 being multiplied n times, and then multiplied 1 extra time.
For the second line, 9 n is factored out from both terms. This leaves 1 behind from the first term and 9 behind from the second term.
Damn, it Was so simple to prove
Log in to reply
I know, right? And still I didn't know how to prove it.
Log in to reply
Same here, maybe we should have tried..
Log in to reply
@Alan Laifer – I just don't understand so.......
Can we get a more verbose explanation?
can someone explain this to me?
I'm very lost here. Could someone explain this to me?
ehm, ain't it obvious enough what he did? O_o
9^(a+b)=9^a*9^b is on of the most basic rules of potences. in this case we have a=n, b=1. then we pull 9^n out of everything
9 n + 9 n + 1 = 9 n + 9 n × 9 = 9 n × ( 1 + 9 ) = 9 n × 1 0
For any positive integer n :
-
9 n ends with 9 if n is an odd integer
-
9 n ends with 1 if n is an even number.
Now, take any two consecutive integers. In that two definitely one is an even number and one is an odd number.
So, here we will take 9 n and 9 n + 1 . If 9 n is odd then 9 n + 1 is even. So the last digit of first one will be 1 and the last digit second one will be 9 . And there sum will give 1 + 9 = 1 0 . If 9 n is even then 9 n + 1 will be odd and the last digits will get interchanged. So there sum will be 9 + 1 = 1 0 .
So, in any case 9 n + 9 n + 1 will be a multiple of 1 0 as it will end up with digit 0 .
Your explanation is not as per the problem creator supposed us to do.
Log in to reply
If you can tell where my solution lacks explanation I will try to improve my solution
Log in to reply
You can see Brian Moehring solution which is pretty clear.
So, in any case 9 n + 9 n + 1 will be a multiple of 10 as it will end up with digit 0 .
This is not intended (I guess) to be explained. Yeah, the numbers are the multiple of 10 however, of what
You proved only that it is a multiple of 1 0 , not that it is specifically 1 0 × 9 n
You go off track when you confuse the even/odd parity of n, n+1 with even/odd parity of 9^n, 9^(n+1). That's a fixable error.
If fixed, you would have proven that 9^n + 9^(n+1) is a multiple of 10.
That's a weaker statement than the statement of the question.
Log in to reply
No it makes perfect sense, the same parity would apply in both instances.
Log in to reply
This is an odd hill to die on, but no, it's not true that the parity is the same. No matter what non-negative integer value of n you choose, the final digit of 9 n will either be 1 or 9 (quoting Ram's solution here), which means it'll be odd, never even.
That is, "If 9 n is odd, then 9 n + 1 is even" is false, but a reading of the rest of the problem shows he meant "If n is odd, then n + 1 is even", and the next two sentences follow.
9 n + 9 n + 1 = 9 n × 1 0 9 n 9 n + 9 n 9 n + 1 = 9 n 9 n × 1 0 1 + 9 = 1 0
Therefore, this statement is always true for any positive integer n .
Thats the solución thats majes more sensei ti me
Using mathematical induction,
Let P(n) be the case that 9^n + 9^(n+1) = 9^n x 10 , n is positive integer
when n = 1, as shown in the question, is true
Therefore the base case is true
Assume true for n=k, i.e. 9^k + 9^(k+1) = 9^k x 10 -- (1) , k is positive integer
To prove true for n=k+1, i.e. need to show that 9^(k+1) + 9^(k+2) = 9^(k+1) x 10
LHS = 9^(k+1) + 9^(k+2) = 9(9^k) + 9(9^(k+1)) = 9(9^k + 9^(k+1))
Substituting (1) into LHS,
LHS = 9(9^k x 10) = 9^(k+1) x 10 = RHS
Hence, the (k+1)th case in true.
Therefore since P(0) is true, and P(k+1) is true => P(k) is true, by Mathematical Induction, the above equation is true for any positive integer n
9 n + 9 n + 1 = 9 n ( 1 + 9 ) = 9 n × 1 0
For any x, it is true that x + 9x = 10x. If x = 9^n, then 9x = 9^n * 9, or 9^{n+1}. This means that the original equation is in the form of “x + 9x” making the result 10x.
Divide both sides by 9 n and you will see that this leads to a correct statement.
9 n + 9 n + 1 = 9 n ∗ 1 0 ⟺ 1 + 9 = 1 0
9 n + 9 n + 1 = 1 × 9 n + 9 × 9 n = 9 n ( 1 + 9 ) = 1 0 × 9 n
9 n + 9 n + 1 = 9 n × 1 0 9 n 9 n + 9 n + 1 = 9 n × 1 0 1 + 9 n + 1 − n = 1 0 1 + 9 = 1 0
The expression is indexed by a natural number n, thus we can use mathematical induction to show the result holds for all natural numbers.
First, let P(n) denote the statement given.
Basis Step: P(0) LHS: 9^0 + 9^1 = 10 RHS: (9^0) x 10 = 10 LHS = RHS thus P(n) holds true for n = 0.
Inductive Step: P(K), P(K + 1) Assume the statement holds true for some natural number K, that is,
9^K + 9^(K + 1) = (9^K) x 10. (I)
Now, we want to show the statement P(K +1) holds, that is,
9^[(K) +1] + 9^[(K + 1) + 1] = (9^[(K) + 1]) x 10.
If we multiply equation (I) by 9, we get
9.(9^K) + 9.[9^(K + 1)] = 9.(9^K) x 10
Now, if we utilise laws of indices from elementary algebra in secondary school
“(a^b).(a^c) = (a^[b + c]) for all real numbers a, b and c”
we obtain
9^[(K) +1] + 9^[(K + 1) + 1] = (9^[(K) + 1]) x 10.
Conclusion: Thus, we have shown for all natural numbers K and K + 1 (including zero in this instance) that the statement P(n) holds true. And so, it has been proven by mathematical induction.
By the Induction Principle:
We probe 9 n + 9 n + 1 = 9 n ∗ 1 0 for n = 0:
9 0 + 9 0 + 1 = 9 0 ∗ 1 0 ⟹ 1 + 9 = 1 0
Then we assume (1) 9 n + 9 n + 1 = 9 n ∗ 1 0 true and probe for (n+1): 9 n + 1 + 9 n + 2 = 9 n + 1 ∗ 1 0
9 n + 1 + 9 n + 2 = 9 ∗ 9 n + 9 ∗ 9 n + 1 = 9 ∗ ( 9 n + 9 n + 1 ) ⟹ b y ( 1 ) = 9 ∗ ( 9 n ∗ 1 0 ) = 9 ∗ 9 n ∗ 1 0 = 9 n + 1 ∗ 1 0
And QED.
If you like mods then here's the solution...
9 is congruent to -1 mod 10... Consider to cases... i) n is even ii) n is odd
i)If n is even... then 9^n is congruent to (-1)^an even number which is 1 If n is even.. it implies n+1 is odd.. which implies 9^n+1 is congruent to (-1)^an odd number which is -1 Hence 9^n + 9^n+1 = 1-1 = o mod 10
ii) Through similar arguments we find that 9^n + 9^n+1 = -1 + 1 = 0 mod 10
Therefore 9^n + 9^n+1 is always divisible by 10
10 = 9 + 1
Substituting this into the equation provided yields:
9^n + 9^{n + 1} = 9^n \times (9 + 1) 9^n + 9^{n + 1} = 9^{n + 1} + 9^n
Apologies, the markdown syntax doesn't seem to work on mobile.
Theoretically we can prove it by principle of mathematical induction.
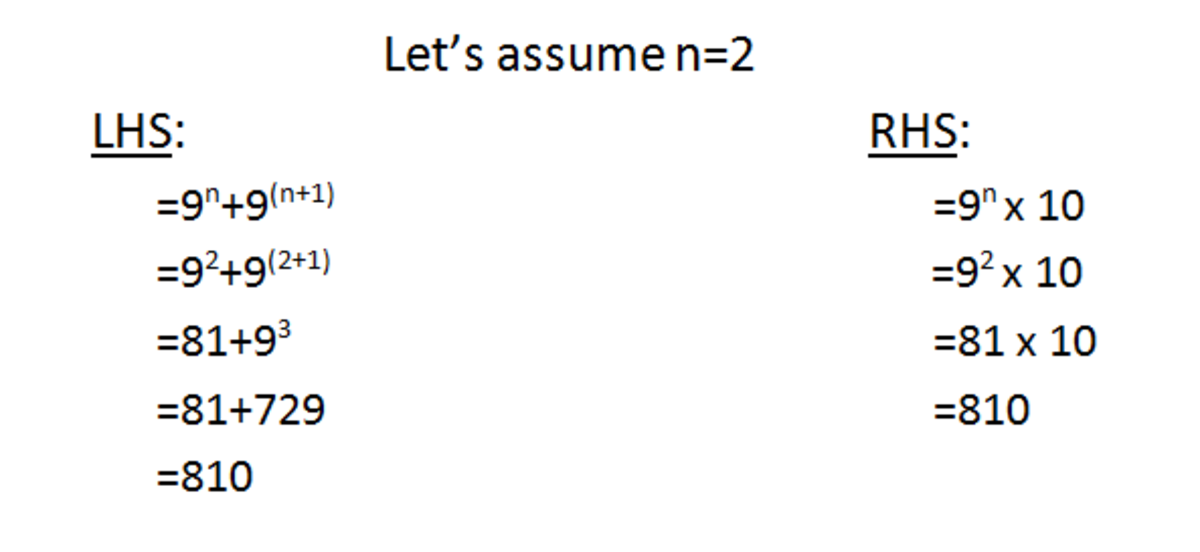
9 n + 9 n + 1 = ( 9 n × 1 ) + ( 9 n × 9 ) = 9 n × ( 1 + 9 ) = 9 n × 1 0