Aditya's Challenges In Number Theory

Assume that $m+n=4k$ for a positive integer $k$ . Therefore, we have $m^2+mn+n^2=49k$ .

Now, $m^2+2mn+n^2=\left(m+n\right)^2=16k^2$ .

Hence, $mn=16k^2-49k$

Since, $mn>0$ , we can say that $k>3$ .

$mn=\left(\frac{m+n}{2}\right)^2-\left(\frac{m-n}{2}\right)^2$

We have: ${ \left( \frac { m-n }{ 2 } \right) }^{ 2 }\ge 0$ .

By AM-GM, we have: ${ \left( \frac { m+n }{ 2 } \right) }^{ 2 }-mn={ \left( \frac { 4k }{ 2 } \right) }^{ 2 }-\left( { 16k }^{ 2 }-49k \right) \ge 0$

From this, we get: $k\le 4$

Hence, $k=4$ .

Hence $\boxed{m+n=16}$ .

The equality occurs when $m=10,n=6$ or vice versa.

Let $x=\gcd(m,n)$ . We can rewrite using $m=ax$ and $n=bx$ for some relatively prime integers $a$ and $b$ .

The fraction becomes:

$\dfrac{ax+bx}{(ax)^2+(ax)(bx)+(bx)^2} = \dfrac{4}{49}$

$\dfrac{a+b}{x*(a^2+ab+b^2)} = \dfrac{4}{49}$

Now, since $a$ and $b$ are relatively prime, $\gcd(a+b,a^2+ab+b^2)=\gcd(a+b,(a+b)^2-ab)=\gcd(a+b,ab)=1$ .

Thus $4|(a+b)$ and $(a^2+ab+b^2)|49$ .

Clearly, since $a$ and $b$ are positive integers, $a^2+ab+b^2 \neq 1$ . Furthermore, $a^2+ab+b^2=7$ gives $a=1$ and $b=2$ (or vice versa), which does not satisfy $4|(a+b)$ . So $a^2+ab+b^2=49$ . In turn, we must have $a+b=8$ .

Plugging back into the original fraction gives $\dfrac{8}{49x} = \dfrac{4}{49}$ and $x=2$ .

Finally, the question asks for $m+n=(a+b)*x=8*2=\boxed{16}$ .

I used Python to solve this question:

Once the program was ran it yielded:

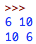
$6 + 10$ is $16$ therefore, the answer is $16$