This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
18 solutions
Sorry I’m trying to write a solution but when I enter the special code to make square roots it just shows the code in preview not a square root sign how am I supposed to do it
Log in to reply
If you're trying to use LaTeX:
Backslash followed by ( to start.
Then type your code, like \sqrt{27}
finish with backslash followed by )
2 7
Jason -- You and all the staff at Brilliant ROCK. :-) JLO
So, I guess what you're saying is that you simply assumed that figure ABC was, in fact, a triangle and thus, AC was a straight line? It would have been better to state that.
Log in to reply
True, the problem had that assumption, without which there is no unique answer... And it'd be better to state it. You can try adding a report, so that Aidan (or one of the Staffs) will be made aware and hopefully fix that.
<ABD=<ADB=60.<DBC=<DCB=30. SO,<BAC=60. so,abd is a equilateral triangle. so,ad=3. then comes sir pythagoras. is this way okay?
Let's complete the illustration in the following way:
We rotated, the original triangle around point
D
, with
1
8
0
degrees. Rotation keeps the lengths and angles, therefore there is a right angle at
B
′
. The angles at
A
and
C
are equal and add up to
1
8
0
degrees, so they are both
9
0
degrees. This makes
A
B
C
B
′
a rectangle.
The diagonals of a rectangle cut each other in half, so
A
D
=
D
C
=
3
. We know that
A
B
=
A
D
=
3
.
For ABC we use the Pythogorean Theorem:
A
B
2
+
B
C
2
=
A
C
2
3
2
+
B
C
2
=
6
2
, therefore
B
C
=
2
7
I'm curious how we can determine that D is the mid point of AC such that the rotated triangle lines up perfectly to become a rectangle, specifically so before any calculations have been done.
Log in to reply
For the record, i did it like this: BCD being an isosceles triangle, angles BCD and CBD are equal. ABD = 180° - BDC = BCD + CBD. But BDA is also an isosceles triangle, so ABD = ADB = 2 * DBC. So ABC = 90° = 3 * DBC, which means DBC = 30°, ABD = 60°, so ABD is an equilateral triangle, so AD = BD = 3.
But yeah, Icarus' solution is missing this part.
But you didn't show that the diagonals would intersect at D ...
Let CBD = x. Then ADB = CBD+BCD = 2x. ADB = ABD = 2x.
ABC = ABD + CBD = 3x, Hence, x = 30.
Hence, triangle ABD is an equilateral triangle. Hence, AD = DC = 3, meaning that D is the mid point of AC
Let x = ∠ B A D . By angle sum of △ A B C , ∠ B C D = 9 0 ° − x . As base angles of isosceles triangle △ B C D , ∠ C B D = 9 0 ° − x . Since ∠ A B C = 9 0 ° , ∠ A B D = x . As base angles of isosceles triangle △ A B D , ∠ A D B = x .
All three angles of △ A B D are x , so it is an equilateral triangle, which means A B = A D = B D = 3 . This means A C = 6 , and by Pythagorean's Theorem on △ A B C , B C = 6 2 − 3 2 = 2 7 .
Did the same. Short and Simple. Upvoted !
I can understand that the angle CBD=90-ABD. But why angle CBD=90-x?
Log in to reply
First you have to see that ∠ B C D = 9 0 ° − x . This is because ∠ B A D + ∠ B C D + ∠ A B C = 1 8 0 ° from the angle sum of △ A B C , and since ∠ B A D = x and ∠ A B C = 9 0 ° , we have x + ∠ B C D + 9 0 ° = 1 8 0 ° , which simplifies to ∠ B C D = 9 0 ° − x .
Then since B D = C D , then as base angles of an isosceles triangle, ∠ B C D = ∠ C B D . Since ∠ B C D = 9 0 ° − x , ∠ C B D = 9 0 ° − x as well.
by geometric mean theorem BD^2= AD x DC
THEN
AD=3=BA
BY PGT
BC= 27^({1/2})
Moderator note:
The geometric mean theorem applies to a diagram like the one below, where h 2 = a b .
Unfortunately, this is only true when h is an altitude! B D and A C are not perpendicular, so the theorem does not apply.
Bravo. I do like this one.
But you can't use the geometric mean theorem, since BD is not an altitude... -.-
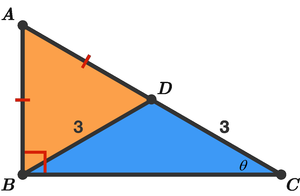
Let ∠ A C B = ∠ D B C = θ . Then ∠ A D B = 2 θ = ∠ A B D , since A B = A D . And we have:
∠ A B D + ∠ D B C 2 θ + θ 3 θ ⟹ θ = 9 0 ∘ = 9 0 ∘ = 9 0 ∘ = 3 0 ∘ .
Therefore, B C = 2 × 3 cos θ = 6 cos 3 0 ∘ = 3 3 = 2 7 .
Less fractions if you go from ∠ A C B = ∠ D B C = θ to ∠ A D B = 2 θ so ∠ A B D = ∠ A D B = 2 θ , etc. ;-)
Chew-Seong --- I am bogged down trying to understand why (angle)ADB is twice that of (angle)ACB. I know that there has to be a geometrical rule that shows that but I do not recall it. Thanks in advance for any and all info.
Log in to reply
In Euclidean geometry, the sum of angles in a triangle is 180°, and so is the sum of two supplementary angles. Because of these two facts, there's a theorem that states that an external angle of a triangle (in this case ADB) is equal to the sum of the other two angles of the triangle (in this case DBC and DCB).
This is how I calculated too👍
Let AB = AD = x, then by Pythagoras theorem, AB^2 + BC^2 = (AD + DC)^2 => x^2 + BC^2 = (x + 3)^2 => x^2 + BC^2 = x^2 + 6x + 9 => BC^2 = 6x + 9
Now, the given options are: 1. 5 = sqrt(25) 2. sqrt(26) 3. sqrt(27) 4. sqrt(28)
Square all of them and subtract 9: 1. 25 - 9 = 16 2. 26 - 9 = 17 3. 27 - 9 = 18 4. 28 - 9 = 19
Since, BC^2 - 9 is a multiple of 6, the rquired answer is 18
Why would x have to be an integer though? o.O
Because the pink triangle is equilateral, as shown by the dashes, we can safely assume that the entire triangle (blue+pink) is a 30-60-90 triangle. The shorter side is 3 units long, and the hypotenuse is 6, leaving BC to be s q r t 2 7
The dashes only mean that it's an isosceles triangle, doesn't HAVE to be equilateral...
Log in to reply
It really looks like it. Just eyeballing it, you can easily tell.
Log in to reply
You're aware that "eyeballing" is not a valid method of reaching an acceptable solution, i hope? :-D
Log in to reply
@C . – yes. That's a really bad idea. (I was calling myself out for that when I was working on the problem, but I did it anyways.)
Log in to reply
@Dylan Daniel – Between you and me, i also went with my gut feeling of it being equilateral and got the correct answer before i proved that part... But afterwards i did stay on it until it "clicked" before i looked at how other people proved it. :-)
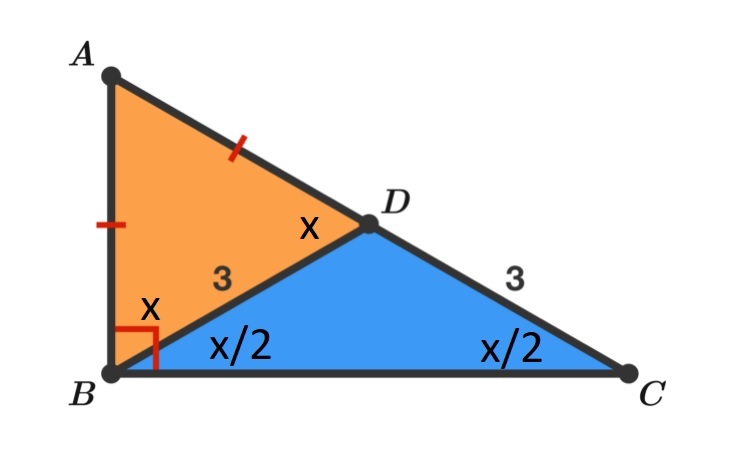 Angle ADB is an exterior triangle to the blue triangle. Exterior angles have the same measure as the sum of the 2 remote interior angles of the blue triangle. If we call angle ADB x, then both angles DBC and DCB must be x/2 since the blue triangle is isosceles, and these 2 angles must be congruent. Since triangle ADB is also isosceles, angle ABD must be x also. This gives us the equation x+ x/2 = 90
Angle ADB is an exterior triangle to the blue triangle. Exterior angles have the same measure as the sum of the 2 remote interior angles of the blue triangle. If we call angle ADB x, then both angles DBC and DCB must be x/2 since the blue triangle is isosceles, and these 2 angles must be congruent. Since triangle ADB is also isosceles, angle ABD must be x also. This gives us the equation x+ x/2 = 90
Solving for x we find x=60 degrees, which means triangle ADB must also be equilateral, and triangle ABC must be a 30-60-90 triangle. AB is 3, so BC must be 3 times the square root of 3, which equals the square root of 27.
Every right-angled triangle can be complemented into a rectangle. Since rectangle can have circle described, every right-angled triangle can have aswell. Thus, d ( D , A ) = d ( D , C ) = d ( D , B ) , where d is a distance function and D is associated with a center of a circle which describes the triangle. This implies that ∣ A B ∣ = ∣ A D ∣ = 3 and triangle A B D is equilateral with angles equal to 60°. This implies that angle D B C = 9 0 ° − 6 0 ° = 3 0 ° = angle D C B , since B C D is isosceles. Now drop a height from point D of triangle B C D . Let ∣ B C ∣ = 2 a where a is a half of ∣ B C ∣ . Using trig. function we have: c o s ( 3 0 ° ) = h y p o t e n u s e a = 3 a = > 2 a = 6 c o s ( 3 0 ° ) = 5 . 1 9 6 1 5 . . . = s q r t ( 2 7 ) )
Triangle ABD is equilateral all sides = 3. The hypotenuse of the larger triangle line AC is therefore 6. Using the equation that the square of the hypotenuse of a right angled triangle (ABC) is equal to the sum of the squares of the other two sides the solution is revealed.
given 3 and other side is also 3 and qouent so nearset value is 27
I assumed that the triangle comes inside a semicircle with the right angle corner touching the circumference of the circle. As the distance to that point is 3, I assumed that , that is the radius and solved using Pythagoras theorem, and got the right answer. I am right???
Create a circle centered on D, because DB=DC, so C and B both on the circle. Now we need to prove A is on the circle. Assume BA intersect with the circle on A’. Now if we can prove ABC is the same as A’BC, the we proved A is on the circle. We have Angle C = Angle C, angle B = angle B and BC = BC. So we can say ABC is the same as A’BC, so we proved A’ is on the circle. The we have q = 3, then we have angle BDC = 60, then we have every angle and length in the picture.
Nice approach. The only thing i kind-of feel you rushed through was showing that angles CBA and CBA' are equal. :-B
<DBC = <DCB, isosceles triangle. 2*<DBC = <ABD, since the sum of the first 2 angles = 180 - <ADB = <ABD, isosceles triangle, so <ABD = 60, and AD = 3. So BC= sqrt(36 - 9) = sqrt(27). Ed Gray
This problem utilizes the Pythagorean Theorem. To start, B D is 3 units long. A B D is an equilateral triangle, so we can conclude that A B and A D are also 3 units long. Now, we can use the Pythagorean Theorem, which is a 2 + b 2 = c 2 . We can see that D C is also 3 units, so let’s add up it and A D to get the Hypotenuse, 3 + 3 = 6 . Now, bringing that up a power of 2, we get 36. Now, we have A B , which is 3. Of course, 3 2 is 9. Now, since we are working backwards, we can conclude that our operation is subtraction, which leaves us with c 2 − a 2 = b 2 . 3 6 − 9 = 2 7 , so we can conclude that B C is 2 7 .
Yeah, the solution comes easily after stating that ABD is an equilateral triangle... But why is it? :-B
Log in to reply
I still haven’t gotten that far in any course except for the first course you’re supposed to do, (Mathematical Fundamentals,) so I Unfortunately am too much of an idiot to answer that question. Edit: I did get it a bit far in Logic, but then I quit halfway through and switched to Algebra Fundamentals.
Log in to reply
A possible approach is determining that it has one angle of 60°, as Chew-Seong Cheong or David Vreken did, or we could use Z Zhao's approach of starting with a circle centered on D of radius 3. Good luck going through the next courses you'll go for. ;-)
Log in to reply
@C . – I'd rather give algebraic proof. Not just measurements.
Log in to reply
@Dylan Daniel – But all of those are algebraic (or geometric, but NOT based on just measuring a diagram)...
Since one of the dimension is 3 than all dimension have to be a multiple of 3 and since 27 is the only number that is a multiple of 3 then that’s the final answer
Let angle ABD=ADB=x,then angle BDC=180-x and angle BDC=90-x,since BD=DC,angle DBC=DCB x=60 solving further will be BD =3 since equilateral triangle hence BC=√27
I think you meant angle DBC=90-x, and you typo'ed, because otherwise it's contradicting what you had just said: that angle BDC=180-x. :-B
Let E be the midpoint of BC. The triangle CDE is similar to ABC. Let x be the length AD. Let y be the length BC. We can write y x + 3 = y 6 .
Cancelling the Ys, we obtain x + 3 = 6
Hence x is 3.
y, or BC can be found by pythagoras’s Theorem, 3 2 + y 2 = 6 2 .
Therefore y = √ 2 7 .
Drop a perpendicular from D to side B C and call the new point E ; since triangle B D C is isosceles, it gets bisected into two congruent triangles.
Let a be the measures of B E and E C . Let q be the measures of A B and A D .
By angle-angle similarity, right triangles D E C and A B C are similar. We know from E C ( a ) corresponding to B C ( 2 a ) that the scale factor is 2.
This also means, based on D C and A C corresponding, that 3 ( 2 ) = 3 + q . So q = 3 , and triangle A B C has a hypotenuse of 6 and a leg of 3. By the Pythogarean Theorem the remaining leg is 6 2 − 3 2 = 2 7 .