Adventitious Quadrangle 2
What is the measure of angle x (in degrees)?
The answer is 40.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
17 solutions
You also obtain the same cyclic quadrilateral upon intersecting the 2 sides of the quadrilateral.
I feel so dumb after seeing this. I used trig, cause all my construction failed.
How do you find the angles after drawing in a second diagonal?
Log in to reply
use the fact that it is cyclic. construct a circle passing through all 4 vertex and use inscribe angle theorem.
https://en.wikipedia.org/wiki/Inscribed_angle#Theorem
Could you explain the cyclic part, like why is it a cyclic quadrilateral?
Edit: Oh I got it. The opposite angles are supplementary i.e. sums to 180. That is enough to prove they are cyclic!
Log in to reply
yes thats correct.
Yep, both necessary and sufficient conditions (that is to say, if one condition fits then so does the other).
how do you get the results of angles of your second step?
Log in to reply
use the fact that it is cyclic. construct a circle passing through all 4 vertex and use inscribe angle theorem.
https://en.wikipedia.org/wiki/Inscribed_angle#Theorem
Log in to reply
@Albert Lau Isn't it more helpful to say that you're using the subtended angle property of the arc, not specifically the inscribed angle theorem?
wow great - Tnks
wow indeed!
i did the same thing. taking reflections works well sometimes.
sorry it is rotation not reflexion.
Log in to reply
Sorry, it is not reflexion but reflection.
Log in to reply
thank you.
What an elegant solution!
After you swing those two triangles what makes you sure that they don't overlap?
Log in to reply
we can choose how much we rotate each triangle, and make sure they dont overlap.
for example, since the angle between the equal sides is 120 deg, we rotate each by 60 degree.
Log in to reply
I wash you had alphabetically marked the vertices so I could tell you that we need to prove that those triangles will fit next to each other.
Log in to reply
starting from left, we will fix the red triangle and rotate blue triangle by 120 degrees around point A. to do this,
-
construct line A D 2 such that ∠ C A D 2 = 6 0 ∘ .
-
construct line C D 2 such that ∠ A C D 2 = 2 0 ∘ .
-
intersect the two lines at point D 2 , Δ A C D 2 and Δ A C 2 D are congruent by ASA.
-
A B C D 2 is cyclic quadrilateral that is used in following steps.
is this rigorous enough?
Log in to reply
@Albert Yiyi – Yes thank you. It is clear now.
You can't rotate each by 60 degree, if you look closely you will see that you have rotated the blue triangle by 80 degree and the red one by 40 degree.
Log in to reply
@Seyed Seyedy – i can rotate both triangles about the intersection point of diagonals, red 60deg counterclockwise, blue 60deg clockwise, such that the equal sides coincides.
besides 80+40 = 120, which is still valid, the triangle wont overlap, the cyclic quadrilateral will be formed regardless.
im not sure i fully understand what's your doubt, can you elaborate more?
@Seyed Seyedy Short answer: we are sure the triangles do not overlap, because the sides of each corresponding triangle that we are putting together are the same length. We know they are the same length, because they (the two sides) form an isosceles triangle in the original figure.
How would you know that the purple triangle are congruent?
Log in to reply
Log in to reply
Owhhh thanks!
What is SAS?
Log in to reply
@Steve Cau – it is one way to proof 2 triangles are congruent. there are 5 ways in total. (SSS, SAS, ASA, AAS, RHL)
here's a link if u need more info:
https://www.mathsisfun.com/geometry/triangles-congruent-finding.html?ref=binfind.com/web
I'd say that is just telling, not really a "hint"...but Mr. Steve Cau has convinced me otherwise
This is beautiful
how did u think of this? this is sexy
Log in to reply
thanks! i use computer program to generate 4 given angles and check if x is rational (using trig). after it output, i try to solve it without using trig, i post only those i can solve it. most i cant (without trig), but here is another one i did solve (without trig), u might like it.
https://brilliant.org/problems/hard-easy-geometry-problem/?ref_id=1509851
hats off to the thinking level
how do you draw diagonal and know the angle?
Log in to reply
we know that quadrilateral is cyclic (why?) , we can draw a circle that passes all 4 vertices, and apply inscribed angle theorem.
https://en.wikipedia.org/wiki/Inscribed_angle
Hi guys, I’m confused on why Albert chose to make the angles 20 and 40 when drawing the diagonal and doing the angle bisect theorem. I know that the theorem states that a central angle is twice the inscribed angle subtending the same arc, but I don’t understand how that’s applied here. Why was that diagonal drawn that way?
Log in to reply
Look at the 40 and 20-degree angles at the bottom of the quadrilateral.
the theorem has another usage: 2 inscribed angles which subtends the same arc are equal. 20,40 deg came from bottom.
since alot of ppl are asking this, i add a circle to help visualize it. hopefully that helps.
This is nice. However, I was wondering whether might be any shorter way of doing this. If you let the other angle (the one that turned out to be 20°) be y, then x + y = 60. Right way I was thinking that x : y = 40 : 20, the same as the ratio of the known angles in the respective triangles. Is there any deeper reason as to why?
Log in to reply
that does not always hold. rotate the digram and view from other 3 directions, the ratios are not equal.
The problem should be under "Advanced." If it had only involved "angle chasing" and the like, then this would have been the appropriate category.
Log in to reply
it is done only involved "angle chasing", some of the solution below gives more such solution, as long as no trigonometry is used.
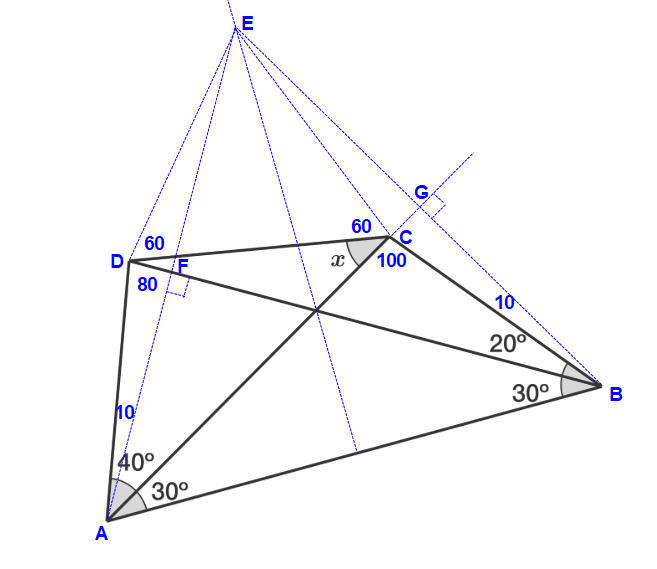
First, fill in the angles that can be determined by triangle sum and straight angles, and also label the vertices A , B , C , D , and E as follows:
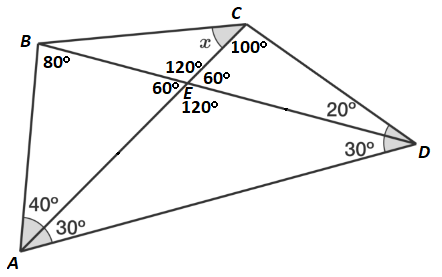
Since ∠ E A D = ∠ E D A = 3 0 ° , △ E A D is an isosceles triangle, and E A ≅ E D .
Next, construct equilateral triangle △ F E D , with C on E F , and fill in the angles:
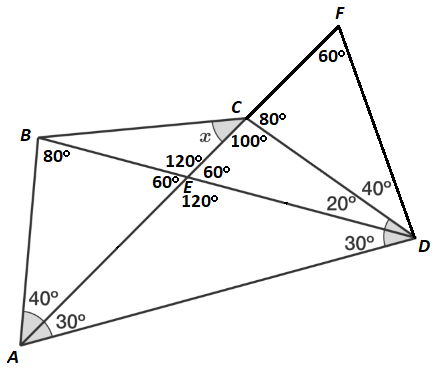
Since F D ≅ E D by equilateral triangle sides, and E D ≅ E A (from above), F D ≅ E A . Since ∠ B E A = ∠ C F D = 6 0 ° and ∠ B A E = ∠ C D F = 4 0 ° , △ D F C ≅ △ A E B by ASA congruence. Therefore, B E ≅ C F .
Finally, construct equilateral triangle △ E C G , with G on E D , and fill in the angles:
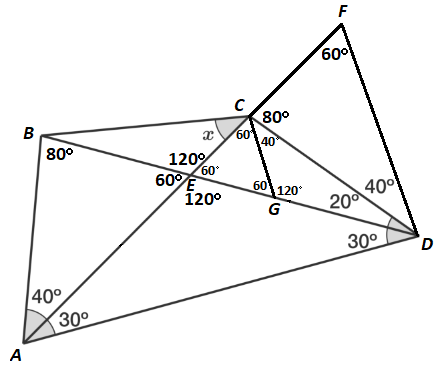
Since E C ≅ E G by equilateral triangle sides, and E F ≅ E D by equilateral triangle sides, E F − E C ≅ E D − E G , or C F ≅ G D . From above, B E ≅ C F , so B E ≅ G D . Since C E ≅ C G by equilateral triangle sides, and ∠ C E B = ∠ C G D = 1 2 0 ° , △ B E C ≅ △ D G C by SAS congruence. Therefore, ∠ B C E = ∠ D C G = 4 0 ° , which means x = 4 0 ° .
awesome solution!
awesome use of construction!
The solution that I understand more, though.
Nice work!
amazing construction. i tried in this way. but did not have confidence to continue. then changed and tried other way and solved it. in this problem we can see lot of equilateral triangles.
this solution i like. here we are looking at side length and use congruence theorems.
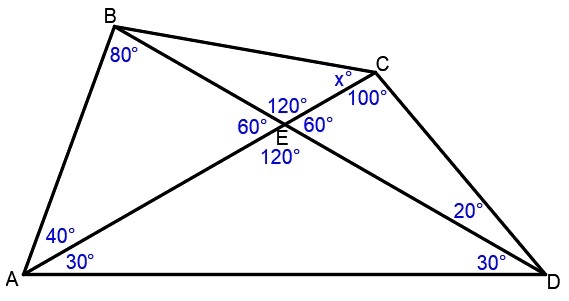 Solution using trigonometry.
Solution using trigonometry.
Consider isosceles △ A D E . Let A E = E D = 1 . Apply cosine law.
( A D ) 2 = ( A E ) 2 + ( E D ) 2 − 2 ( A E ) ( E D ) ( cos 1 2 0 )
( A D ) 2 = 1 + 1 − 2 ( cos 1 2 0 )
A D ≈ 1 . 7 3
Consider △ A B D . Apply sine law.
sin 3 0 A B = sin 8 0 A D
A B = sin 8 0 sin 3 0 ( 1 . 7 3 ) ≈ 0 . 8 8
Consider △ A C D . Apply sine law.
sin 5 0 A C = sin 1 0 0 A D
A C = sin 1 0 0 sin 5 0 ( 1 . 7 3 ) ≈ 1 . 3 5
Consider △ A B C . Apply cosine law.
( B C ) 2 = ( 0 . 8 8 ) 2 + ( 1 . 3 5 ) 2 − 2 ( 0 . 8 8 ) ( 1 . 3 5 ) ( cos 4 0 )
B C ≈ 0 . 8 8
Since B C = A B , △ A B C is isosceles. Therefore,
x = ∠ B A C = 4 0 ∘
exactly my way haha
This solution gets you to x is approximately 40 degrees. Is there a way to refine the trigonometry--maybe playing around with the sine and cosine laws--to prove equality?
Log in to reply
working it out without approximating the lengths, i.e. using surd and trigonometric notation, we get to the point where BC is exactly equal to AB
Log in to reply
I worked it out as well, but following those steps outlined in this proof you need to use the trig facts that sin(50) = cos(40), sin(80) = sin(100), and sin(30)=1/2 .
Some solutions really opened up my vision towards Geometry. I will give a rather mundane approach, which I exploit in most of the angle-chasing problems.
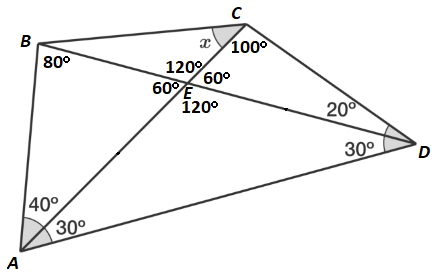
@David Vreken forgive me for using your image. I totally forgot how to draw these neat images online.
Considering △ A B C , we have from sine-formula, A B sin x = B C sin 4 0 .
Again, in △ D B C , we have B C sin 2 0 = B D sin ( 1 0 0 + x ) .
Finally, in △ A B D , we have B D sin 7 0 = A B sin 3 0 .
We see that, on multiplying the above relations likewise, the denominators cancel out. That is the motivation to use this approach.
So we get,
sin x ⋅ sin 2 0 ⋅ sin 7 0 = sin 4 0 ⋅ sin ( 1 0 0 + x ) ⋅ sin 3 0
⇒ sin x ⋅ sin 2 0 ⋅ sin 7 0 = ( 2 ⋅ sin 2 0 ⋅ cos 2 0 ) ⋅ sin ( 1 0 0 + x ) ⋅ 2 1
Remembering, sin 7 0 = cos 2 0 and cancelling common terms on both sides, we are left with
sin x = sin ( 1 0 0 + x )
⇒ sin x − sin ( 1 0 0 + x ) = 0
⇒ 2 ⋅ cos ( x + 5 0 ) ⋅ sin ( − 5 0 ) = 0
⇒ cos ( x + 5 0 ) = 0 ( Since sin 5 0 ∘ = 0 )
⇒ x = 4 0 ∘ .
By creating a symmetrical triangle based on ADC, reflected along AD, angle x can be ascertained from resulting triangle ABC'.
we cant be certain that B D 1 C is a straight line. it must be proven first.
in fact if we can prove it, we can use whatever the prove method is, to show ∠ A D 1 B + ∠ A D 1 C = 1 8 0 ∘ , x will be trivial to find from here.
Log in to reply
Then we can't be sure any of the lines are straight which is a bit silly because it is fair to imply that they all are even if it isn't stated.
BD1C is forced to be a straight line (not least by construction) because if it is not the triangles do not reflect.
Log in to reply
im sorry i dont think u understand, what i mean straight line, i mean collinear. reflecting A D 1 C has nothing to do with point B or D 1 B , they are not forced to be a straight line.we cant imply that they are collinear.
in fact are u suggesting that for any position B we can be certain C 1 D 1 B is always a straight line?
Log in to reply
@Albert Yiyi – or lets assume ur method is valid. i have a similar problem here.
https://brilliant.org/problems/hard-easy-geometry-problem/?ref_id=1509851
i have oriented ur solution appropriately so that it align with this problem.
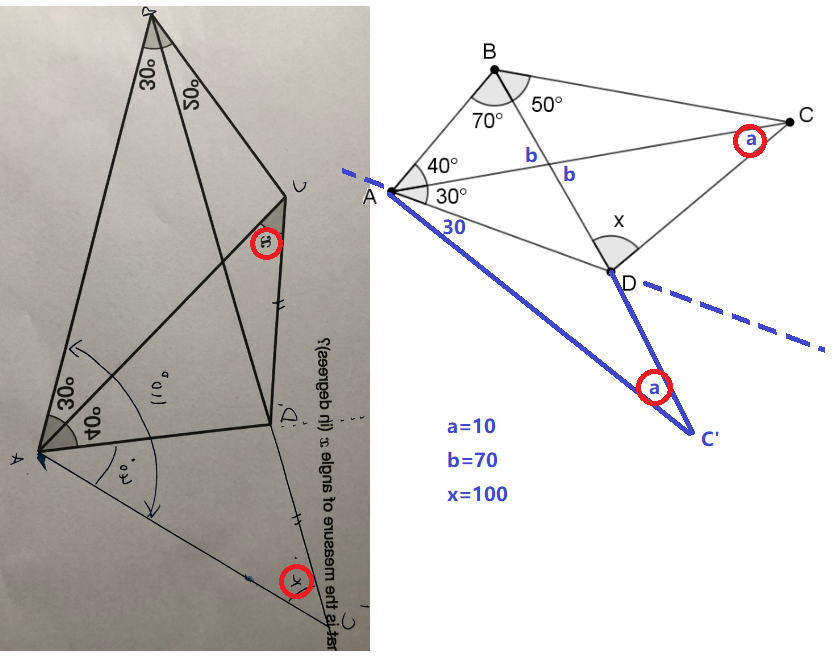
by ur method, i reflect ADC to ADC', and found a=80, x=100, but the correct answer is x=80.
in fact we can see visually ADC' isnt congruent to ADC at all, a true reflection would make C'DB obviously not collinear.
Beautiful.
I concur with @Albert Lau , how do you know that C'D aligns with BD ?
Your solution seems to be independant of ∠ C B D . What if we increase it, preserving △ A B D and ∠ B A C ? then AC increases in length without changing direction, x decreases, and both ∠ A D C and ∠ A D C ′ increase, but ∠ A D B does not change. That should make clear C', D and B are not necessary aligned ?
What am I missing in your proof here ?
That's beautiful
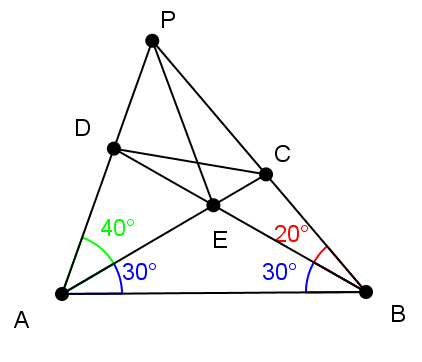 Let
E
=
A
C
∩
B
D
and
P
=
A
D
∩
B
C
.
D
P
C
E
is a cyclic quadrilateral, then
∠
D
C
E
=
∠
D
P
E
.
By Ceva's Theorem
sin
∠
E
A
P
sin
∠
B
A
E
⋅
sin
∠
E
P
B
sin
∠
A
P
E
⋅
sin
∠
E
B
A
sin
∠
P
B
E
=
1
sin
4
0
∘
sin
3
0
∘
⋅
sin
E
P
B
sin
∠
A
P
E
⋅
sin
3
0
∘
sin
2
0
∘
=
1
Finally
∠
A
P
E
+
∠
E
P
B
=
6
0
∘
and
sin
4
0
∘
sin
∠
A
P
E
=
sin
2
0
∘
sin
∠
E
P
B
implies
∠
A
P
E
=
4
0
∘
.
Let
E
=
A
C
∩
B
D
and
P
=
A
D
∩
B
C
.
D
P
C
E
is a cyclic quadrilateral, then
∠
D
C
E
=
∠
D
P
E
.
By Ceva's Theorem
sin
∠
E
A
P
sin
∠
B
A
E
⋅
sin
∠
E
P
B
sin
∠
A
P
E
⋅
sin
∠
E
B
A
sin
∠
P
B
E
=
1
sin
4
0
∘
sin
3
0
∘
⋅
sin
E
P
B
sin
∠
A
P
E
⋅
sin
3
0
∘
sin
2
0
∘
=
1
Finally
∠
A
P
E
+
∠
E
P
B
=
6
0
∘
and
sin
4
0
∘
sin
∠
A
P
E
=
sin
2
0
∘
sin
∠
E
P
B
implies
∠
A
P
E
=
4
0
∘
.
this can be done without trig. continue from ur solution at ∠DCE = ∠DPE:
∠AEB = 2∠APB, by inscribe angle theorem AE=PE=BE, so in isosceles ΔAEP we have ∠DPE = 40°. therefore ∠DCE = 40°.
this construction is actually pretty clean.
Log in to reply
You are right, finally is only see that E is the circumcenter of APB and we are done.
This is not texting. Spell out "your."
This will be another way to construct auxiliary lines.
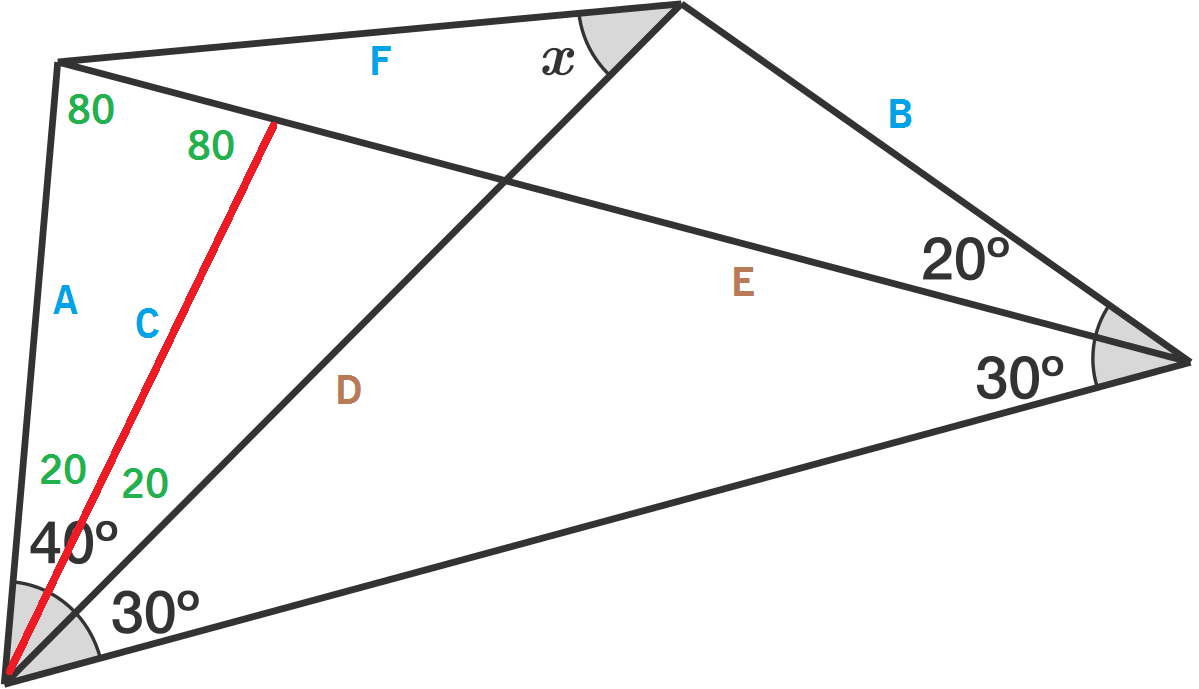 After looking long enough at the diagram, it feels very tempting to show somehow that A=F or B=F, and proving either of these will give the value of the angle.
After looking long enough at the diagram, it feels very tempting to show somehow that A=F or B=F, and proving either of these will give the value of the angle.
So the natural goal is to produce as many isosceles or equilateral triangles as possible, using side lengths the length of either A, B, or F. Here's how I did:
First construct C. Now the triangles between C-D and E-B are identical, so C=B. The 80° angles give A=C, therefore A=B.
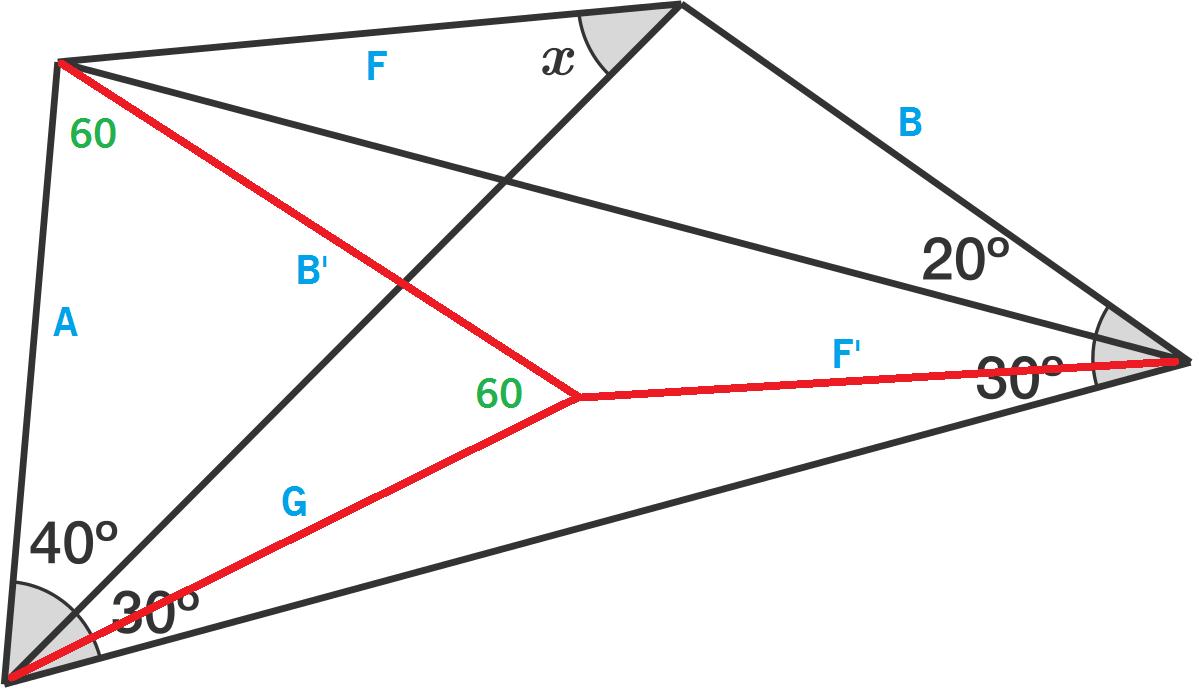 Next, move B closer to A, creating a parallelogram BFB'F' and an equilateral triangle AB'G.
(
∠
A
B
′
=
∠
A
B
=
1
8
0
∘
−
7
0
∘
−
5
0
∘
=
6
0
∘
)
Next, move B closer to A, creating a parallelogram BFB'F' and an equilateral triangle AB'G.
(
∠
A
B
′
=
∠
A
B
=
1
8
0
∘
−
7
0
∘
−
5
0
∘
=
6
0
∘
)
By the inscribed angle theorem, B', F', and G form a set of radii of a same circle, thus B'=F'.
Immediately A=B=F, where the pair A=F can give the desired x = 4 0 ° .
nice solution. however i believe there is something need to be cleared.
"move B closer to A" by creating parallelogram, we dont have degree of freedom to choose 60 deg between A and B', the fact that angle is 60 deg needs to be proven.
Not sure why this is not upvoted but im pretty sure this is my favourite
Geometry solution:
Draw equilateral triangle ABE . See sketch below for the positions of points D,F,C,G,E and values of angles ∠ (DAE)= 10, ∠(CBE)=10, ∠(ACB)=100,∠(DCE) =60,∠ (ADB)=80 Since AC and BD are angle bisector of ∠(BAE) and ∠(ABE) so AC is the perpendicular bisector of BẸ Triangle ACE congruent to triangle ACB ( case SAS) so ∠(ACB)= ∠(ACE)= 100 degrees and x= 100-60= 40 degrees
Answer using trig:
Firstly, I used the properties of an isosceles triangle to take both AE and BE as 1 unit in length. I then used basic angle rules to obtain all angles labelled.
Using the sine rule twice to find some useful side lengths:
s i n ( 2 0 ) E C = s i n ( 1 0 0 ) 1
E C ≈ 0 . 3 4 7
s i n ( 6 0 ) D E = s i n ( 8 0 ) 1
D E ≈ 0 . 6 5 3
Using the cosine rule to find the final side length:
( C D ) 2 = ( E D ) 2 + ( E C ) 2 − ( 2 × E D × E C × cos 1 2 0 )
C D ≈ 0 . 8 7 9
Then used the sine rule once more to find angle x:
0 . 6 5 3 s i n ( x ) = 0 . 8 7 9 s i n ( 1 2 0 )
∴ x = 4 0 ∘
Like everyone else, I started with angle hunting.
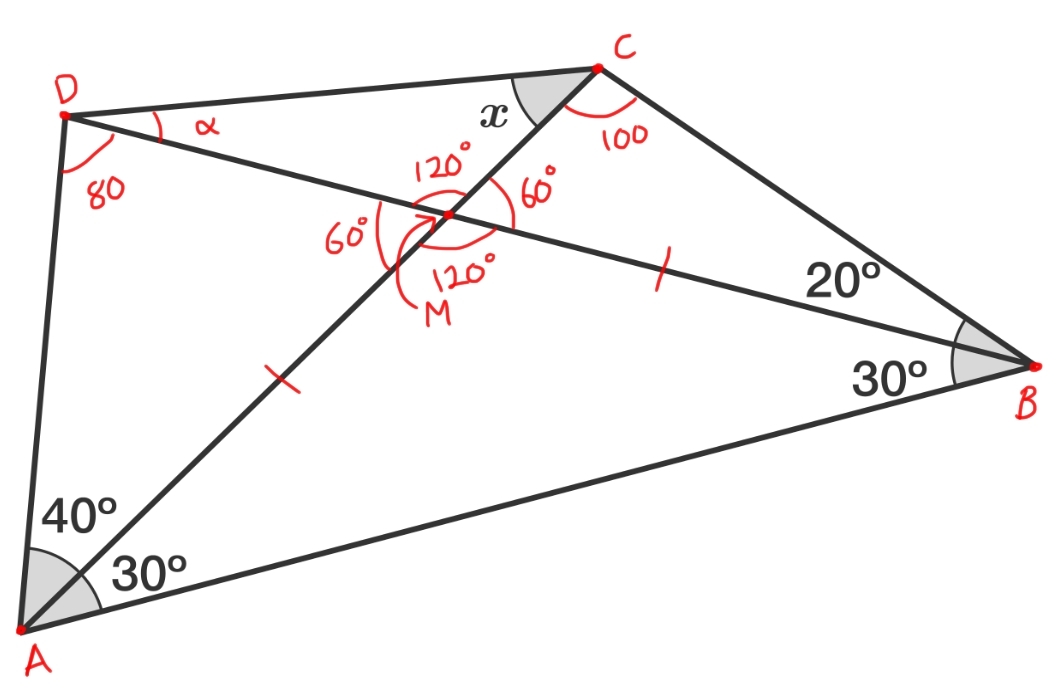
First note that 1 2 0 + x + α = 1 8 0 and thus, x + α = 6 0
Using the sine law in triangles DMA and CMB,
A M = D M sin ( 4 0 ) sin ( 8 0 )
B M = C M sin ( 2 0 ) sin ( 1 0 0 )
Since triangle AMB is isoceles, A M = B M
D M sin ( 4 0 ) sin ( 8 0 ) = C M sin ( 2 0 ) sin ( 1 0 0 )
C M D M = sin ( 2 0 ) sin ( 8 0 ) sin ( 1 0 0 ) sin ( 4 0 )
80 and 100 are complementary angles, so sin 8 0 = sin 1 0 0 and they cancel out in the fraction.
Resulting: C M D M = sin ( 2 0 ) sin ( 4 0 )
Using the sine law again but in triangle CMD,
sin x D M = sin α C M
C M D M = sin α sin x
sin α sin x = sin ( 2 0 ) sin ( 4 0 )
At this point it looks like we're stuck. It's going to be impossible to guess a solution from this.
However, the solution has been right there before our eyes the whole time. Remember x + α = 6 0 ? Well, apparently 4 0 + 2 0 = 6 0
And that also a solution to sin α sin x = sin ( 2 0 ) sin ( 4 0 ) , so...
Therefore, x = 4 0 ∘
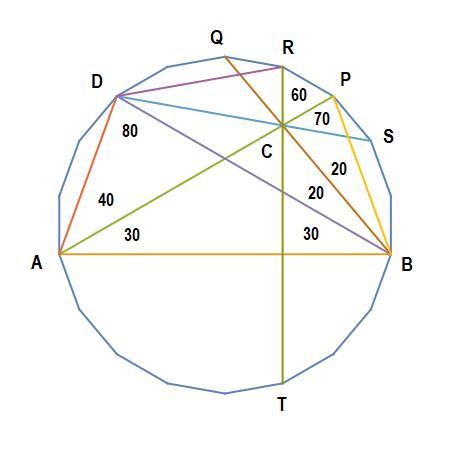
Use a 18-gon for this one. Start by drawing lines R T , P A and Q C , so that triangle Δ R P C is an equilateral triangle, and therefore triangle Δ Q R C is isosceles, with base angles 4 0 degrees. Next, we draw lines C B , P B and A B , so that angle ∠ A P B = 8 0 degrees, and angle ∠ A B P = 7 0 degrees. From this we determine that angle ∠ C B P = 2 0 degrees, and finally that angle ∠ P C B = 8 0 degrees, so that not only triangle Δ B C P is isosceles, line segments Q C and C B are colinear.
Therefore A D = P T = C T = D C . From this, we see that triangle Δ A D C is isosceles, and that angle ∠ D C A = 4 0 .
This proof requires showing that lines R T , P A , Q B , S D intersect at the same point C . See the following:
Here, we'll only look at the question of the concurrency
of lines
A
D
,
B
E
,
C
F
, all meeting (or not) at point
Q
. Those lines, as well as line
A
B
, are drawn in the 18-gon as follows:
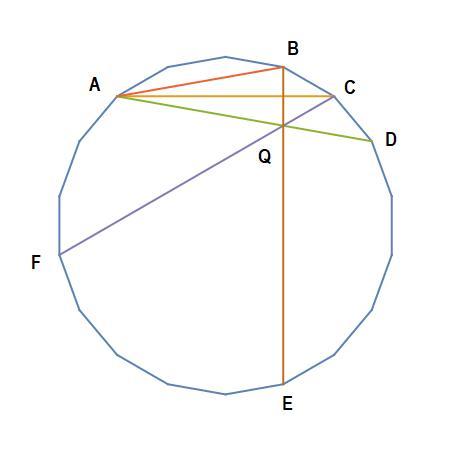
First we draw the symmetrical kite A B C Q , formed by reflection of triangle Δ A B C which has angles 1 0 , 1 4 0 , 3 0 degrees. Thus, we know that not only both triangles Δ A B Q , Δ B C Q are isosceles, Δ B C Q is equilateral.
Then if lines B Q and B E both make the same angle 6 0 from line B C , then both lines are colinear.
Likewise for lines C Q and C F for the same reason.
Finally, if lines A Q and A D both make the same angle 2 0 from line A B , then they are colinear as well.
This establishes the concurency of lines B E , C F , and A D , meeting at point Q .
am i missing something? how do i prove the blue chord is concurrent with other 2 chords? (green and orange)
Log in to reply
also i think one of your 80 degree angle should be 100 degree
I don't know yet, it's late here right now. I'll have a closer look at it tomorrow, and maybe add some more lines.
Okay, the extra lines have been added and proof completed.
Log in to reply
i must have missed something obvious... without A C , how can i prove either ∠ P = 8 0 ∘ or B P = B C ? i can see that granting any one will complete the proof, which might give some insight on how to tackle the 42-gon problem.
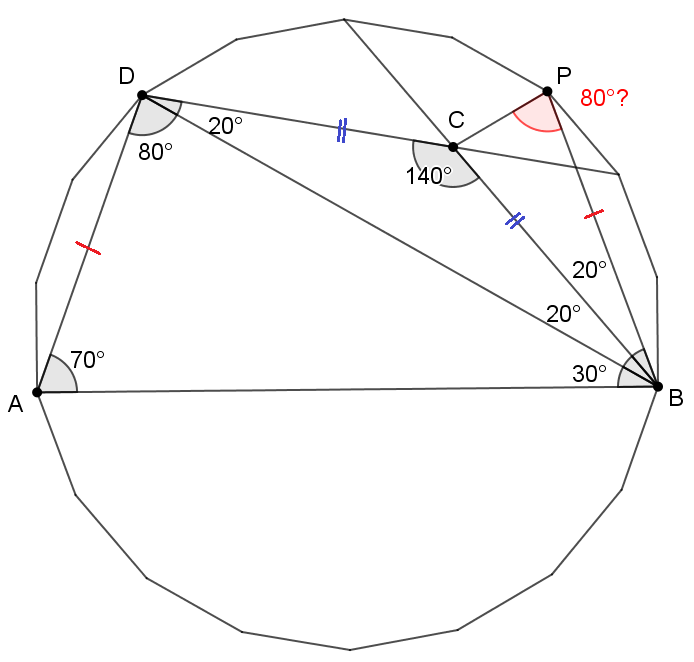
Log in to reply
@Albert Yiyi – (under construction)
Yes, a 42-gon would be the way to go to try to handle the "What's the 7 doing in there?" problem. A 21-gon would not be sufficient.
Log in to reply
@Michael Mendrin
–
i still dont get it, is there a typo somewhere?
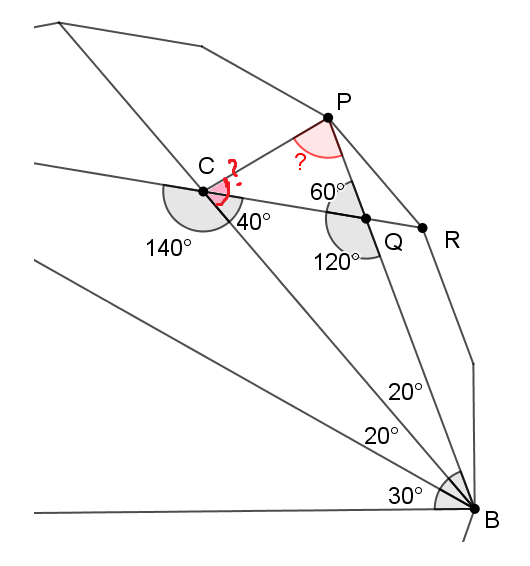
-
∠ C Q P = ∠ P Q C = 6 0 ∘ , both are pointing at the same angle. ∠ P Q C = 4 0 ∘
-
how do i prove ∠ P C B = 8 0 ∘ ? In Δ B C P only 20 degree is known. the other two are unknown?
Log in to reply
@Albert Yiyi – It's 4th of July here.. but let me look at it once again
@Albert Yiyi – Okay, 3rd time around.. how does it look now?
Log in to reply
@Michael Mendrin – thanks for your patience with my constant questions. unfortunately i feel like that doesnt work too.
both ∠ C B P = 2 0 ∘ or ∠ T C B = 4 0 ∘ cannot be justified because Q C B has not proven to be collinear yet (marked different color).
Therefore, in Δ C B P only one angle is known.
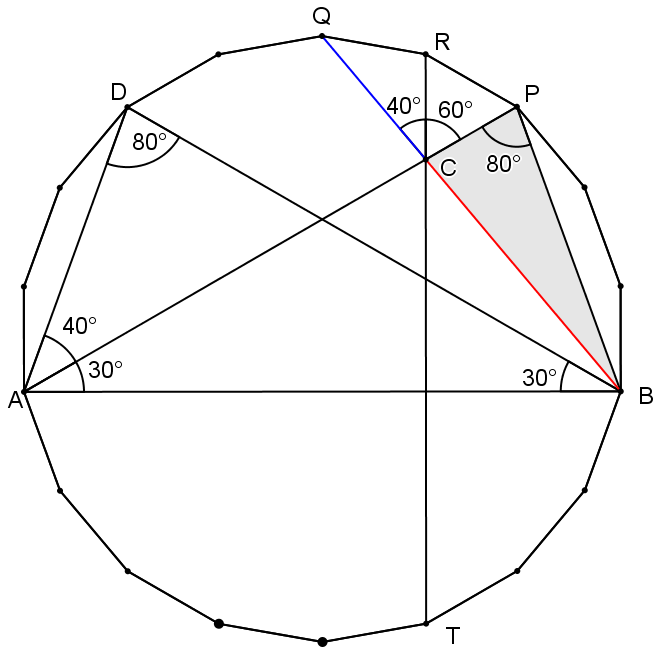
12-gon works because the kite ensures 3 lines concurrent at 90 degrees vertex. but in general, im inclined to believe that proving 3 lines concurrent is as hard as finding the required angle itself.
Log in to reply
@Albert Yiyi – Okay, see my added comments in my solution about that.
I feel writing this solution as this one is really incredible!!! credits : Dong Kwan Choo
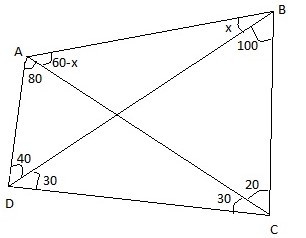
We have, A D A B A B B C C B C D C D D A = 1 so by sine rule, sin x sin 4 0 sin 2 0 sin ( 6 0 − x ) sin 3 0 sin 1 0 0 sin 8 0 sin 3 0 = 1 o r sin x sin ( 6 0 − x ) = 2 1 sec 2 0 o r , cot x = 1 + sec 2 0 3 from above equation sove for x to get x = 4 0
I used brute force. The lower left corner is (0,0) and the lower right corner is (1,0). The upper left corner is (x1,y1) and the upper right corner is (x2,y2). The equations are y1/x1=tan 70° , y1/(1-x1)=tan 30° ; y2/x2=tan 30° ; y2/(1-x2)=tan 50° ; The slope of the upper line is (y2-y1)/(x2-x1), The angle is -10°. So x=40°. The J-code is this.
't3 t5 t7'=.3 o. o. 180%~ 30 50 70
y1=.t7*x1=.%1+t7%t3
y2=.t3*x2=.%1+t3%t5
(30+30)-30+t^:_1 (y2-y1)%x2-x1
40
It's about thinking outside the box:
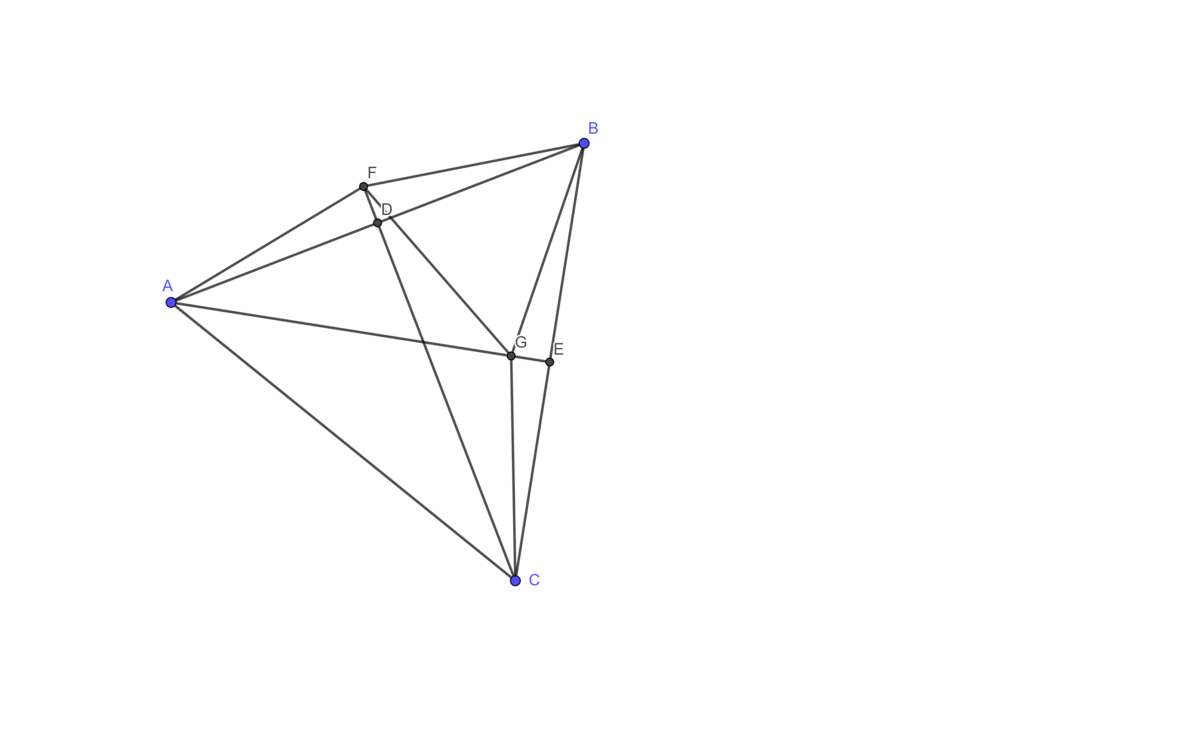 A
B
C
is an equilateral triangle (the side length doesn't matter since everything can be scaled to 1) with bisectors
C
D
and
A
E
. Now consider the affine transformation that rotates 10° clockwise and scales to
B
G
:
B
E
.
This maps
E
to
G
and
D
to
F
. Thus the segment
F
E
forms a
1
0
°
angle to
D
E
. Now our original configuration is simply
A
F
G
C
and the angle
x
is just the (clockwise oriented) angle formed by
E
A
to
G
F
, thus we get
A
B
C
is an equilateral triangle (the side length doesn't matter since everything can be scaled to 1) with bisectors
C
D
and
A
E
. Now consider the affine transformation that rotates 10° clockwise and scales to
B
G
:
B
E
.
This maps
E
to
G
and
D
to
F
. Thus the segment
F
E
forms a
1
0
°
angle to
D
E
. Now our original configuration is simply
A
F
G
C
and the angle
x
is just the (clockwise oriented) angle formed by
E
A
to
G
F
, thus we get
x = ( E A , G F ) = ( E A , E D ) + ( E D , G F ) = 3 0 ° + 1 0 °
x = 4 0 °
I'm guessing there are a lot more nice relationships that follow from this type of strategy
I found what could be coincidental, but if not is just an extremely simple solution.
Lets call the centre O, the point of angle 50° we shall call A, and the point of angle 70° will be called B (therefore for example (here (<) denotes an angle ∠ O A B = 3 0 ∘ = ∠ O B A ).We will also call angle x <CDO (top left=C, top right=D, centre=O, bottom left=B and bottom right=A.
So, with simple geometry rules w find that: <OAB = 30 = <OAB (making OAB an isosceles triangle)
<BOA = 120 = <COD (Vertically opposite angles are equal (VO))
<COB = 60 = <DOA (((360 -(120*2))/2 = 60) and therefore VO)
<BCO = 80 ( Angles in a two dimensional triangle add to 180° (AT))
<ODA = 100 (AT)
Therefore we get that 180 - 120 = <OCD + <ODC, (or x° + y° = 60°)
We can also get that 360 - ( <ODA + <DAB + <ABC + <BCO (100+50+70+80 = 300) = 60.
This is where I made my (likely coincidentally correct) assumption. Based on the fact that ABCD would be a regular trapezium (internal angle = 360), it is almost as if point A has been stretched until <CBO is double <OAD (we can ignore the triangle OBA as they (<CBA and <DAB) share the common angle of 30°). From this I said that because <CBO = 2*<OAD, then x = 2y (I don't quite know how to explain my thought process but it seemed to make sense) so, as x+y = 60, then 3y=60 and y=20, therefore 2(20) = x = 40.
Hence \I found what could be coincidental, but if not is just an extremely simple solution.
Lets call the centre O, the point of angle 50° we shall call A, and the point of angle 70° will be called B (therefore for example (here (<) denotes an angle <OAB = 30° = <OBA).We will also call angle x <CDO (top left=C, top right=D, centre=O, bottom left=B and bottom right=A.
So, with simple geometry rules w find that: <OAB = 30 = <OAB (making OAB an isosceles triangle)
<BOA = 120 = <COD (Vertically opposite angles are equal (VO))
<COB = 60 = <DOA (((360 -(120*2))/2 = 60) and therefore VO)
<BCO = 80 ( Angles in a two dimensional triangle add to 180° (AT))
<ODA = 100 (AT)
Therefore we get that 180 - 120 = <OCD + <ODC, (or x° + y° = 60°)
We can also get that 360 - ( <ODA + <DAB + <ABC + <BCO (100+50+70+80 = 300) = 60.
This is where I made my (likely coincidentally correct) assumption. Based on the fact that ABCD would be a regular trapezium (internal angle = 360), it is almost as if point A has been stretched until <CBO is double <OAD (we can ignore the triangle OBA as they (<CBA and <DAB) share the common angle of 30°). From this I said that because <CBO = 2*<OAD, then x = 2y (I don't quite know how to explain my thought process but it seemed to make sense) so, as x+y = 60, then 3y=60 and y=20, therefore 2(20) = x = 40.
Hence x = 40°
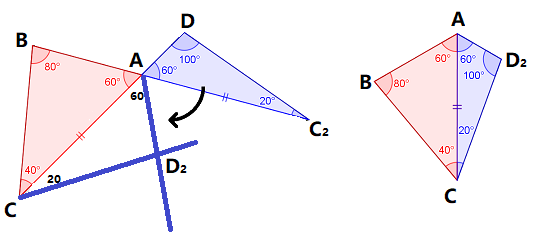
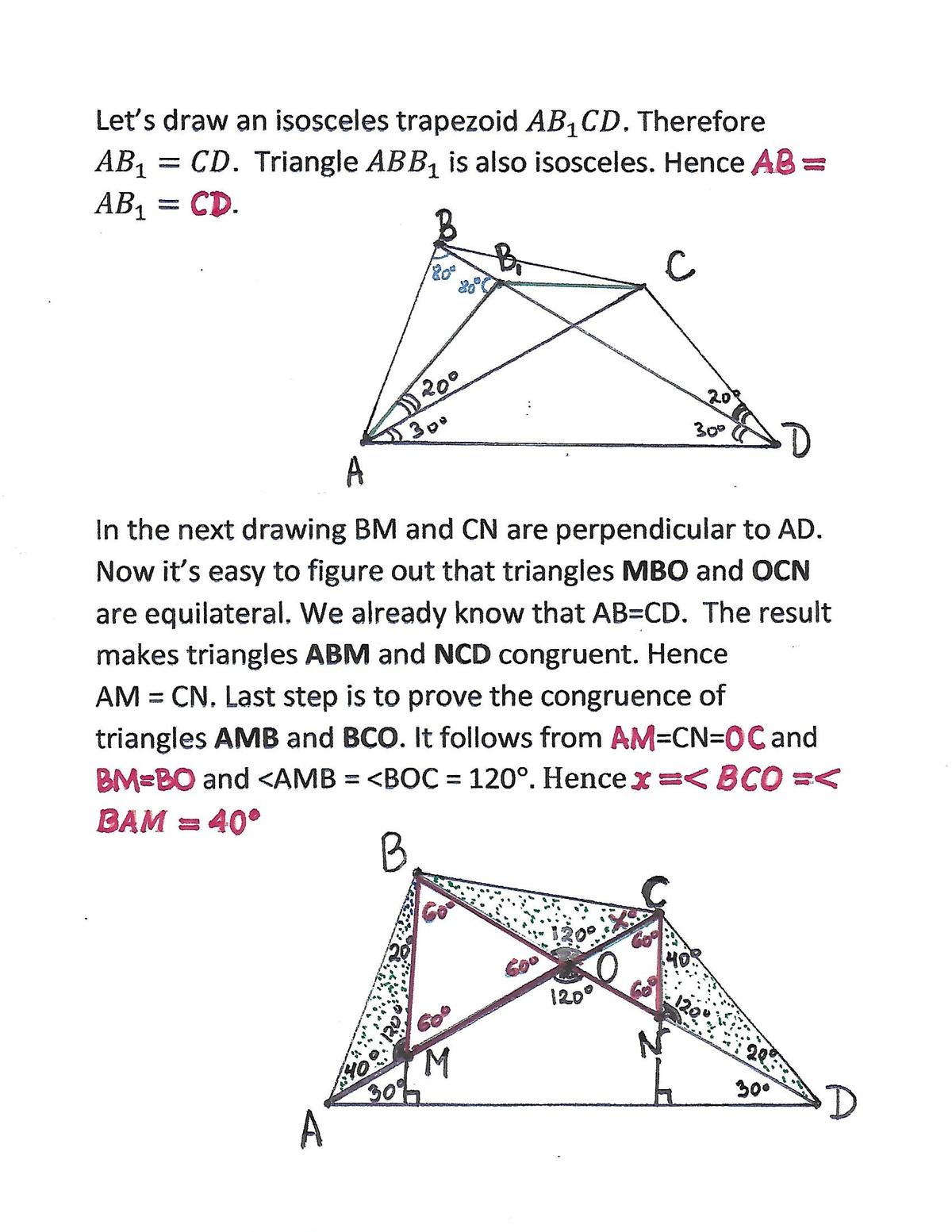
This solution will be attempted without trigonometry.
First, some simple angle chasing. Also its not hard to see there is an isosceles triangle.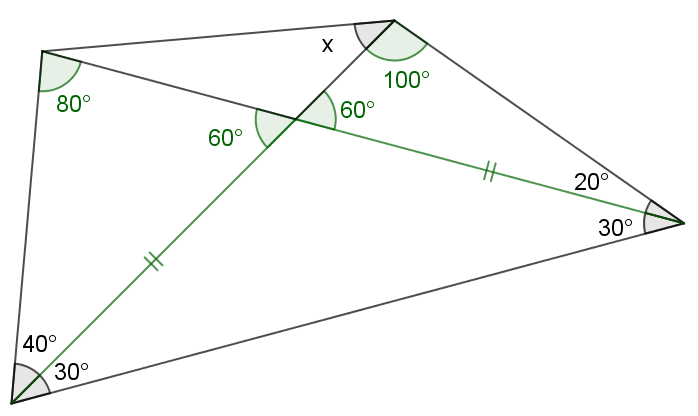 Now, it seems like we are stucked. But If we look long enough, the 80°, 100° supplementary angles are looking more and more suspicious.
Now, it seems like we are stucked. But If we look long enough, the 80°, 100° supplementary angles are looking more and more suspicious.
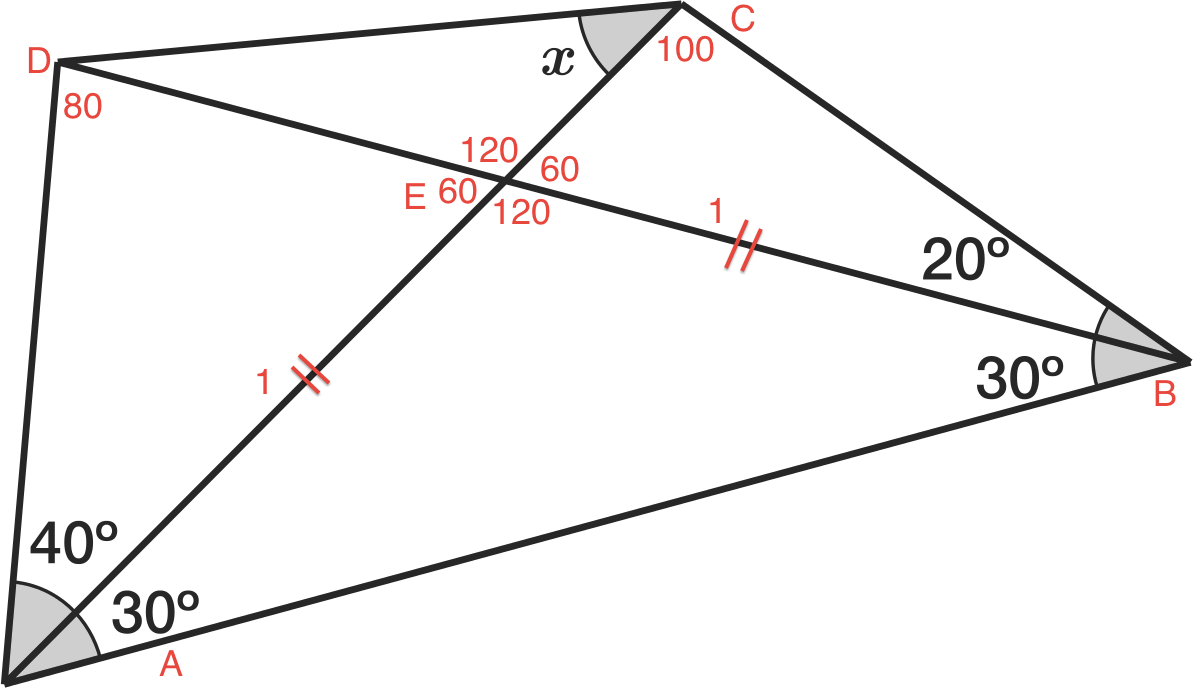
The first trick: what if we "move" two of the triangles such that two of the equal sides coincides?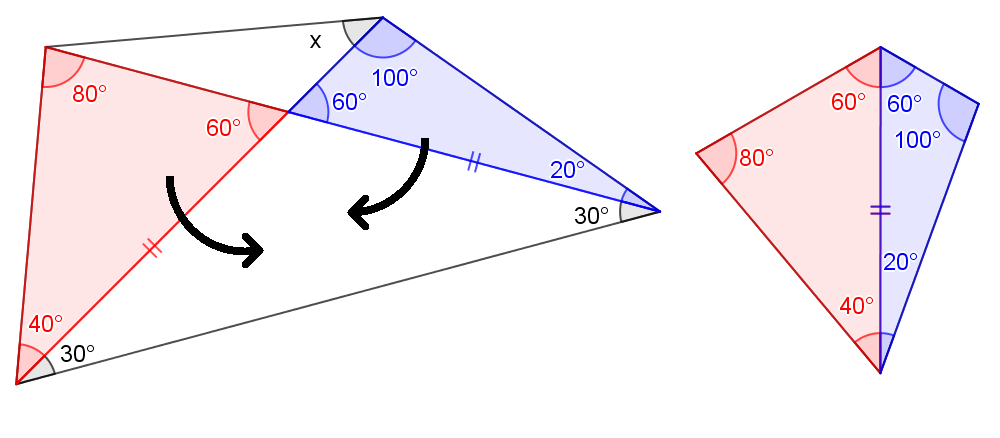 A cyclic quadrilateral is formed. (Why cyclic?)
A cyclic quadrilateral is formed. (Why cyclic?)
Next, draw another diagonal and hunt down all angles. (Inscribed angle theorem.)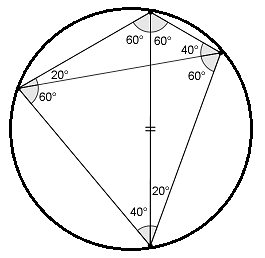 But what is the use of this cyclic quadrilateral?
But what is the use of this cyclic quadrilateral?
The second trick is to realise there is a pair of congruent triangle hidden.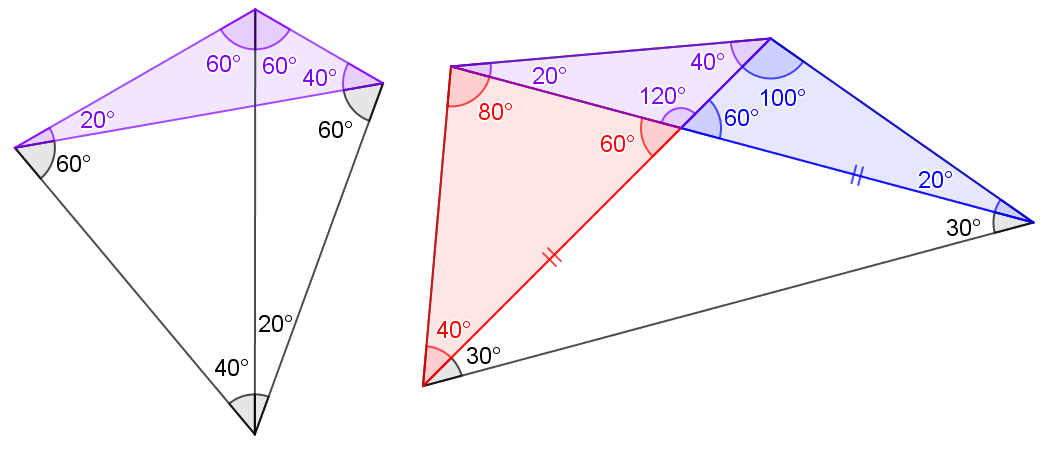 The purple triangles are congruent. (Why so?)
The purple triangles are congruent. (Why so?)
∴ x = 4 0 ∘