Adventitious Quadrangle 3
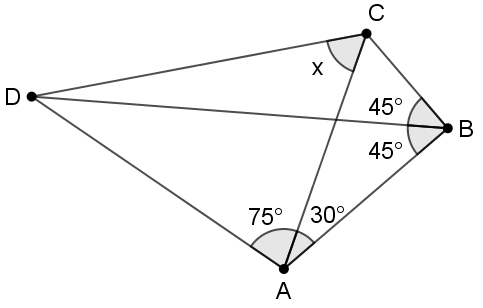
Find x in degrees.
Bonus: Solve without trigonometry.
The answer is 60.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice solution! By the way, how could you make these accurate figures?
geogebra. (its free)
Log in to reply
Log in to reply
i think its the same as this prob
https://brilliant.org/problems/worlds-hardest-easy-geometry-problem/
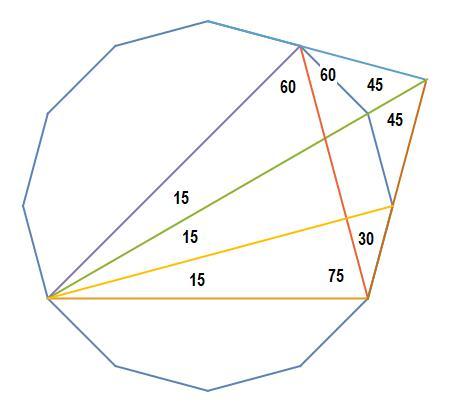
Use a 12 sided regular polyhedron to help with this one and do a bunch of angle chasing. The key to this proof is the symmetrical kite, the one with a right angle vertex.
this is crazy! how did u came out with this solution? did u construct the whole diagram starting from 12-gon, and compare the angles?
Log in to reply
I started with a 12-gon and fit your geometry into it to see what comes out of it. Your figure had a lot of angles that were multiples of 15 degrees, so that suggested the 12-gon.
Log in to reply
thanks! i would never come up that solution myself.
Log in to reply
@Albert Yiyi – Next time you come up with another adventitious quadrillateral, try using a n-gon. If all the angles are multiples of 10, try a 18-gon.
Log in to reply
@Michael Mendrin – im trying one of your problem using 42-gon. i think i found a way, but the missing piece is to prove 3 chords concurrent .
i'm at work currently, i will try when i get home.
edit: 3 chords concurrent.
Log in to reply
Here's a stab at your Adventitous Quadrilateral 2. The key step is proving that triangle to be isoceles.
Isn't drawing triangles trigonometry? Anyway, I know what @Albert Lau means. I am using trigonometry " proper " here.
Let A C and B D intersect at E . We note that △ A B C is a 3 0 ∘ - 6 0 ∘ - 9 0 ∘ right triangle. Let B C = 1 ; then A C = 2 . Let C E = a ; then by sine rule, we have sin 4 5 ∘ a = sin ∠ B E C 1 = sin 7 5 ∘ 1 , ⟹ a = sin 7 5 ∘ sin 4 5 ∘ .
Now, let ∠ C D B = θ and C D = b . By sine rule again,
⎩ ⎪ ⎨ ⎪ ⎧ C E sin ∠ C D B = a sin θ = sin ∠ C E D b = sin 1 0 5 ∘ b = sin 7 5 ∘ b A C sin ∠ A D C = 2 sin ( θ + 3 0 ∘ ) = sin ∠ C A D b = sin 7 5 ∘ b
⟹ a sin θ sin 4 5 ∘ sin θ sin 7 5 ∘ 2 sin 7 5 ∘ sin θ ⟹ tan θ = 2 sin ( θ + 3 0 ∘ ) = 2 sin θ cos 3 0 ∘ + cos θ sin 3 0 ∘ = sin 4 5 ∘ cos 3 0 ∘ sin θ + sin 4 5 ∘ sin 3 0 ∘ cos θ = 2 sin 7 5 ∘ − sin 4 5 ∘ cos 3 0 ∘ sin 4 5 ∘ sin 3 0 ∘ Note that a = sin 7 5 ∘ sin 4 5 ∘
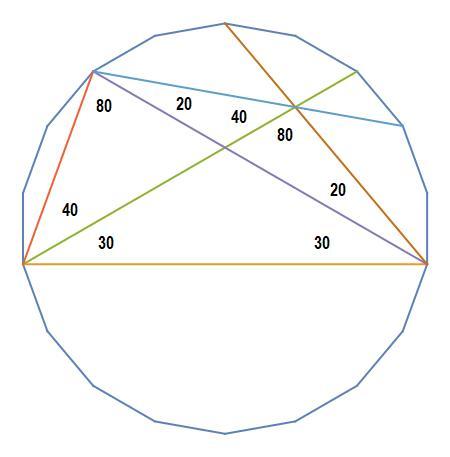
This solution will be attempted without trigonometry.
reflect Δ A B D about A D .
show that C A B ′ is a straight line.
show that Δ B D B ′ is an equilateral triangle.
show that B C D B ′ is cyclic by inscribed angle theorem.
show that x = 6 0 ∘ .