aera of rectangle
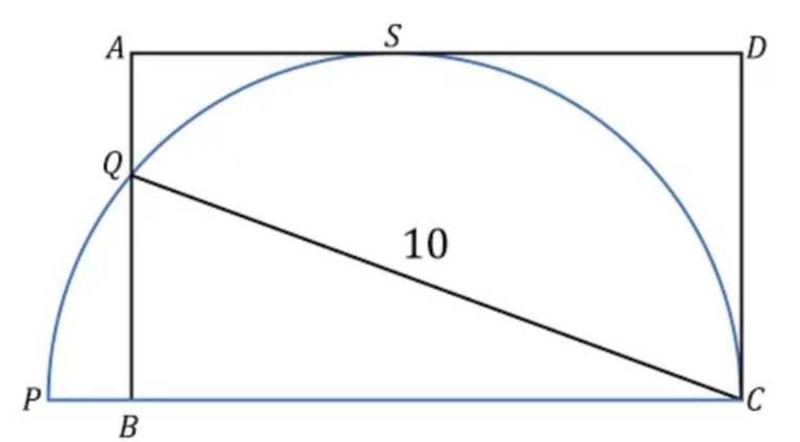
In the figure, P Q S C is a semicircle. Find the area of rectangle A B C D .
The answer is 50.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
same approach! do admire your figure.. especially the perpendicular symbols' 'Q' one "straight lines" and 'B' using a "square".. as 2D orientation is not supprted in "MS paint" lol .. XD
Log in to reply
Thanks. Yes, I am using MS Paint and it does not support non-right-angle rotation. So sometimes I just give up drawing it.
Log in to reply
likewise... but you can try "edraw" software.. it's good for diagrams.. cheers!
Log in to reply
@Nibedan Mukherjee – Thanks. I will check it out.
Log in to reply
@Chew-Seong Cheong – Sir, Hope you are keeping well.. what's the present situation at your place.... stay safe!
Log in to reply
@Nibedan Mukherjee – I am well. Been under lockdown and staying at home for about 2 months now. It is fined to me, I have been working for six years now. Used to it. How about you?
Log in to reply
@Chew-Seong Cheong – sir I'm good , it's not conducive to discuss about it in this interface.. so I'm providing my mail IDs : [email protected] , [email protected] .. hope u don't mind.. thanks
Log in to reply
@Nibedan Mukherjee – My Facebook: https://www.facebook.com/chewseong.cheong Email: [email protected]
Let ∠ Q C B = α . Then, since ∠ P Q C is a semicircular angle, therefore cos α = 2 b 1 0 , where b = ∣ C D ∣ = ∣ S D ∣ = the radius of the semicircle.
Also, cos α = 1 0 l where l = ∣ B C ∣ .
Hence, the required area is l b = cos α 5 × 1 0 cos α = 5 0 .
Let the radius of the semicircle be r . Then the height of rectangle A B C D , A B = C D = r and P C = 2 r . Let the base of rectangle A B C D , B C = b . As P C the diameter of the semicircle, ∠ P Q C = 9 0 ∘ . Then △ P Q C and △ Q B C are similar.
Therefore Q C B C = P C Q C ⟹ 1 0 b = 2 r 1 0 ⟹ b = r 5 0 . The area of rectangle A B C D , A = b r = r 5 0 × r = 5 0 .