Ah, 3 Consecutive Primes make my day!

By contradiction, suppose $\sqrt{2} = a + nd, \sqrt{3} = a + md, \sqrt{5} = a + rd$ for some reals $a,d$ and integers $n,m,r$ . Then

$\sqrt{3} - \sqrt{2} = (m - n)d \Longrightarrow m - n = \dfrac{\sqrt{3} - \sqrt{2}}{d}$ and $\sqrt{5} - \sqrt{3} = (r - m)d \Longrightarrow r - m = \dfrac{\sqrt{5} - \sqrt{3}}{d}$ , so

$\dfrac{r - m}{m - n} = \dfrac{\sqrt{5} - \sqrt{3}}{\sqrt{3} - \sqrt{2}} = (\sqrt{5} - \sqrt{3})(\sqrt{3} + \sqrt{2}) = \sqrt{15} + \sqrt{10} - \sqrt{6} - 3$ .

But as $n,m,r$ are integers, $\dfrac{r - m}{m - n}$ must be rational, yet $\sqrt{15} + \sqrt{10} - \sqrt{6} - 3$ is irrational. So by contradiction, $\sqrt{2}, \sqrt{3}$ and $\sqrt{5}$ cannot be elements of the same arithmetic sequence.

Added proof of the irrationality of $\sqrt{15} + \sqrt{10} - \sqrt{6} - 3$ : As the difference between an irrational and a rational number is irrational, if suffices to prove that $\sqrt{15} + \sqrt{10} - \sqrt{6}$ is irrational. By contradiction, suppose that $\sqrt{15} + \sqrt{10} - \sqrt{6} = a$ for some rational number $a$ . Then $\sqrt{15} + \sqrt{10} = a + \sqrt{6}$ , and upon squaring both sides we find that

$15 + 10 + 2\sqrt{150} = a^{2} + 6 + 2a\sqrt{6} \Longrightarrow 19 - a^{2} = 2a\sqrt{6} - 2\sqrt{25 \times 6} = (2a - 10)\sqrt{6}$ .

Now $19 - a^{2}$ is rational, as is $2a - 10$ , but since $\sqrt{6}$ is irrational $(2a - 10)\sqrt{6}$ is also irrational, (being the product of a non-zero rational and an irrational number), thus providing the desired contradiction. (Note that $\sqrt{15} + \sqrt{10} \approx 7$ and $\sqrt{6} \approx 2.4$ , so $a \approx 4.6$ and thus $2a - 10 \ne 0$ , satisfying the non-zero condition.)

For this proof we're going to use the facts that

addition / subtraction / multiplication / division in nonzero rationals is closed

and

the square roots of positive nonsquare integers (2, 3, 5, 6, etc.) are irrational.

Suppose $\sqrt{2},$ $\sqrt{3},$ and $\sqrt{5}$ are all part of the same arithmetic sequence. Then there must be integers $a$ and $b$ such that

$a(\sqrt{3}-\sqrt{2}) = b(\sqrt{5}-\sqrt{3})$

Letting rational number $R = \frac{a}{b}$ we can write this as

$\begin{aligned} R(\sqrt{3}-\sqrt{2}) &= \sqrt{5}-\sqrt{3} \\ R\sqrt{3}-R\sqrt{2} &= \sqrt{5}-\sqrt{3} \end{aligned}$

Add $\sqrt{3}$ to both sides. This gets the term $(R+1)\sqrt{3}$ where $R+1$ is rational. Let $Q=R+1.$

$Q\sqrt{3}-R\sqrt{2} = \sqrt{5}$

Square both sides.

$3Q^2 + 2R^2 - 2QR\sqrt{6} = 5$

Now we can subtract $3Q^2$ and $2R^2$ from $5$ and the result must be rational.

$-2QR\sqrt{6} = (\text{a rational number})$

We can also then divide both sides by $-2QR$ and the right hand of the equal sign will still be rational.

$\sqrt{6} = (\text{a rational number})$

But since the square root of a nonsquare integer is irrational, this is a contradiction. Hence $\sqrt{2},$ $\sqrt{3},$ and $\sqrt{5}$ must not be part of the same arithmetic sequence. $\square$

Assuming that $\sqrt 2$ , $\sqrt 3$ and $\sqrt 5$ are number of an arithmetic progression with a common difference $d$ . We can assume that $d>0$ without loss of generality. Then the following system of equations is true.

$\begin{cases} \sqrt 2 + md = \sqrt 3 & ...(1) \\ \sqrt 3 + nd = \sqrt 5 & ...(2) \end{cases}$ , where $m$ and $n$ are positive integers.

Then we have $d = \dfrac {\sqrt 3-\sqrt 2}m = \dfrac {\sqrt 5-\sqrt 3}n$ and that:

$\begin{aligned} \frac {\sqrt 5-\sqrt 3}{\sqrt 3-\sqrt 2} & = \frac nm \\ (\sqrt 5-\sqrt 3)(\sqrt 3+\sqrt 2) & = \frac nm \\ \sqrt {15} -3 + \sqrt{10} - \sqrt 6 & = \frac nm \end{aligned}$

Since LHS is irrational and RHS is rational, there is no solution to the above equation and therefore the assumption is false . No , $\sqrt 2$ , $\sqrt 3$ and $\sqrt 5$ are not numbers of an arithmetic progression.

Let's recall the formula for the arithmetic progression: $x_i=a + b*i$ . Which means that if we interpret this formula as a function of i , then all members of the progression are equally spaced laying on the straight line, where a is the vertical shift and b is the slope of this line.

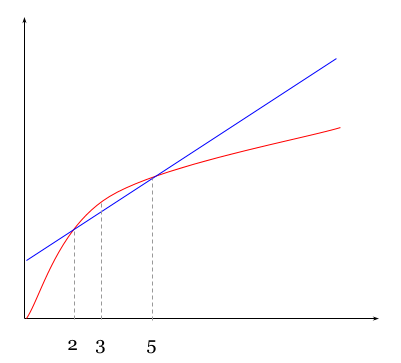
$\sqrt{2}$ , $\sqrt{3}$ and $\sqrt{5}$ are the values of the function $y=\sqrt{x}$ . So, the question is, is it possible to intersect parabola with the straight line in 3 points. The answer is obviously not.

I feel that this proof is somewhat informal. There are other solutions here which are much more logically consistent then mine but they are based on a different ideas. So, I am wondering, how this idea can be turned into a solid mathematical proof.

If $\sqrt{2}$ , $\sqrt{3}$ , $\sqrt{5}$ is arithmetic progression, then must $\frac { \sqrt {3} - \sqrt {2} } { \sqrt {5} - \sqrt {3} }$ = 1

$( \sqrt {3} - \sqrt {2} ) ( \sqrt {5} + \sqrt {3} )$ = 2

$\sqrt {15} + 1$ = $\sqrt {10} + \sqrt {6}$

16 + 2 $\sqrt {15}$ = 16 + $2 \sqrt {60}$

$\sqrt {15} = \sqrt {60}$ , this is wrong.

So, $\sqrt {2} , \sqrt {3} , \sqrt {5}$ not an arithmetic progression.

If we let

$a \approx 1.0461659$
$d \approx 0.462547$
$r \approx 0.937364$

Then

$(a+d)r \approx \sqrt{2}$
$(a+2d)r^2 \approx \sqrt{3}$
$(a+4d)r^4 \approx \sqrt{5}$

hmm...

Note: The form is $(a+dn)r^n$ where $n$ is a positive integer, while $a, d$ both can be irrational. For this problem, $r=1$ , for which there is no solution.

This is similar to saying that: Can 2^2, 3^2 and 5^2 all be numbers in Arithmetic Progession?

Basically, anything to do with manupilating powers of a number will increase and decrease depending on the number.

Eg. 1^2=1 2^2=4 3^2=9 4^2=16 5^2=25

And on an on and on... No common difference

They all need to be whole numbers?

Can’t we just assume that they can’t constitute three numbers in an arithmetic series because the irrationals are densed along the real axis therefore there’s no foreseenable constant gap between them?

As {(√3-√2)/(√5-√3)} is irrational, it can't be in AP.