Algebra or Calculus?
Let x , y and z be real numbers satisfying 5 x + 6 y + 7 z = 8 , find the minimum value of x 2 + y 2 + z 2 .
If your answer is of the form B A , where A and B are coprime positive integers, submit A + B .
The answer is 87.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Great! Nice metjod. Deserves an upvote!
Log in to reply
Tjanks.... :-)
SOMEBODY STOLE MY PROBLEM TITLE
You gotta pay by solving it XDD
Log in to reply
Ahahahahahah. This title is slightly different. It is algebra or calculus :P
Log in to reply
@Aditya Kumar – XD
Still, I can't accept that. 100% of the words are similar XD
Same method (+1).
Nice! I had solved it the geometrical way. I forgot about using Cauchy Schwarz here :p
Log in to reply
Great.... Its always awesome to do a calculus or algebra question the geometrical way.... I also thought about the geometrical solution when I was writing the algebraic one.. ;-P
Log in to reply
Wow! The same thing happened with me!! :)
Log in to reply
@Prakkash Manohar – I used the geometric one too! And when I saw Cauchy Schwarz...'how come I forget this......'
A geometry problem, no algebra here
I'm going to use Lagrange multipliers .
Let L ( x , y , z ) = x 2 + y 2 + z 2 + λ ( 5 x + 6 y + 7 z − 8 ) . For finding a maximum or a minimum of L is necessary d L ( x , y , z ) = 0 ⇒ : d x d L ( x , y , z ) = 2 x + 5 λ = 0 d y d L ( x , y , z ) = 2 y + 6 λ = 0 d z d L ( x , y , z ) = 2 z + 7 λ = 0 ( ∗ ) 5 x + 6 y + 7 z = 8 All this implies that λ = 5 − 2 x = 6 − 2 y = 7 − 2 z Substituing in the last equation we get x = 6 5 y , z = 6 7 y and now substituing in ( ∗ ) we get y = 5 5 2 4 , x = 1 1 4 , z = 5 5 2 8 and substituing these values in A = x 2 + y 2 + z 2 we'll get A = 5 5 3 2 . For seeing it's really a minimum, take the matrix of d 2 L ( x , y , z ) and see is a positive defined matrix...
Yeah this was my method using calculus. Just edit your solution a bit. Instead of d L ( x , y , z ) use partial derivative sign. Oherwise it'll confuse those who are new to it.
Log in to reply
Is it better like this?Maybe I can do the whole proof, if you want it... But It'll confuse more those who are new to it, I think.
By quoting "take the matrix" do you mean the Hessian Matrix ? I think you should add that explanation in as that's not a easy task to check whether it's minimum,maximum or a saddle point there by utilizing the hessian & checking the matrix to be positive definite(Especially for beginners) @Guillermo Templado (Upvoted +1)
Log in to reply
Yes, I mean the Hessian Matrix... the Hessian matrix of d 2 L ( x , y , z ) = ⎝ ⎜ ⎛ 2 0 0 0 2 0 0 0 2 ⎠ ⎟ ⎞ , then d 2 L ( x , y , z ) ( ( h 1 , h 2 , h 3 ) 2 ) > 0 , ∀ h = ( h 1 , h 2 , h 3 ) ∈ R 3 with h = 0
Log in to reply
Yeah Sure , You may add this two lines into your solution so it would be perfect !
Log in to reply
@Aditya Narayan Sharma – Good, it's already added, isn`t it? if someone wants more details he can check Hessian matrix
Log in to reply
@Guillermo Templado – Oh yes I didn't notice ! Calculus is really descriptive in this cases other than classical inequalities. They doesn't really cover every inch of a problem. Like verifying the minima here
Consider Two Vectors
5i+6j+7k
xi+yj+zk
Taking there dot product and setting it equal to product of their magnitudes times cosine of the angle between the two we get
32/55 = (x^2+y^2+z^2)(cosA)
Where A Is angle between two vectors
For Minimum A = 0
Note- i,j,k are unit vectors along coordinate axes
nice but same as rishabh's solution just you have derived cautchy schwarz inequality .upvoted! :-)
Log in to reply
Yeah actually i always forget cauchy inequality so i always do problems by using its derivation only :)
Log in to reply
Ya.. I never remember the cauchy inequality i also derive from vector dot product .
Please elaborate and LaTeX your solution.
Let r = ⎝ ⎛ x y z ⎠ ⎞ and a = ⎝ ⎛ 5 6 7 ⎠ ⎞ , we have r ⋅ a = 8 then ( r ⋅ a ) ( r ⋅ a ) = ( r ⋅ r ) ( a ⋅ a ) = r 2 a 2 = 6 4 therefore r 2 = 3 2 / 5 5 . This is just solving the vector along the plane.
Thanks for sharing your method!
By CS-Inequality we have ( x 2 + y 2 + z 2 ) ( 5 2 + 6 2 + 7 2 ) ≥ ( 5 x + 6 y + 7 z ) 2 = 6 4 . Therefore x 2 + y 2 + z 2 ≥ 1 1 0 6 4 = 5 5 3 2 = b a . Thus a + b = 8 7 .
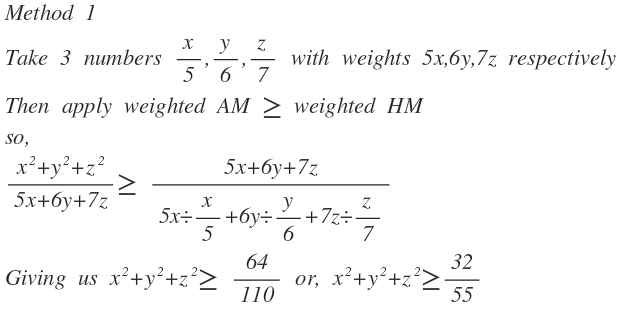


Applying Cauchy Schwarz inequality :- ( x 2 + y 2 + z 2 ) ( 5 2 + 6 2 + 7 2 ) ≥ ( 5 x + 6 y + 7 z ) 2 = 6 4 ⟹ x 2 + y 2 + z 2 ≥ 1 1 0 6 4 = 5 5 3 2 ∴ 3 2 + 5 5 = 8 7 ⋆ ⋆ ⋆ ⋆ ⋆ Equality occurs when: 5 x = 6 y = 7 z
Geometrically we can interpret x 2 + y 2 + z 2 as the squared distance from origin of a point ( x , y , z ) satisfying the equation of plane Π : 1 1 0 5 x + 1 1 0 6 y + 1 1 0 7 z = 1 1 0 8 . And we know this distance is minimum for foot of perpendicular point whose distance from origin is ( 1 1 0 8 ) 2 .