This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
28 solutions
no ,the answer is plus or minus 8
Log in to reply
by definition √ only returns a positive value if the question was x^2 = 8^2 then the answer would be -+8
Log in to reply
Thank you. I never knew that before. I would have said +/-8 as well.
It is not a second degree equation, were you not have a clue for the initial value. In this problem , only -8 is real answer.
Log in to reply
Actually I thought it was -8 too
exactly, that was my reasoning as well
EDIT: Just saw the reason why, ( x ) 2 = x 2
My solution was: ( − 8 ) 2 = ( − 8 ) ( − 8 ) = ( − 8 ) ( − 8 ) = ( 2 i 2 ) ( 2 i 2 ) = 4 i 2 4 = 4 ( − 1 ) ( 2 ) = − 8
an even root from any positive real number has two answers, one is positive and one is negative, because any negative number raised to any even number has a positive answer... That does'nt happen to odd potencies (and roots)
Isnt square root just power 1/2?
The square root operation is not a function because there are always two possible results. A particular number "A" is the square root of another number "B" if A*A=B. Therefore both +8 and -8 are equally correct answers. I have seen many engineering problems in which the negative root has a real world meaning that is useful.
This is wrong. Unless stated or a positive sign precedes the square root sign, then one must assume both solutions, +-8, are valid. I am a maths student at Imperial College London so I know what I am talking about...
In a previous quiz, a problem was given as:
x = -4, sqrt(x^2) = ?
In that quiz question, the correct answer was -4 only. When I entered it into Google, the answer I got was also -4. Can someone explain to me why in this question it is +8?
In the first quiz, I thought that the answer was 4, because: sqrt[(-4)(-4)] = sqrt(16) = 4 I got it wrong. Now, in this quiz, I assumed that the answer was the same as the previous one, as in: sqrt[(-8)^2] = ((-8)^2)^1/2 = (-8)^1 = -8 I got this wrong too... Is there some rule that I should know about?
P.S. I couldn't get the latex code to work, so sorry for the formatting.
I picked the wrong answer choice, but your explanation makes sense. Yes, and the order of evaluation for nested parenthesis is from the inside out: ((-8)^2)^(1/2)) => (64^(1/2))
((-8)^2)^ 1/2 = (-8)^ 1/2= -8
√(x^2)=+-x Well, Brilliant is not so Brilliant xD
The root operation may be defined as the inverse of squaring. As the root undoes the squaring, only -8 is the answer. But, IF you accept the root as being ONLY the positive value of undoing the square, the answer is STILL negative eight. (Plus tim s minus being plus)!
you sore losers suck at math do some AoPS tbh
Per definition; the principle square root of x 2 is the positive value x , not − x . For instance, we take 1 0 0 to be 10, not − 1 0 . .
However, in an equation, the square root can be both the positive and the negative value of x . For instance, x 2 = 1 0 0 → x = 1 0 or x = − 1 0 .
Because this problem doesn't consist of an equation, the correct answer is 8, not -8.
Ok, I get it, but why is it 8? If the square root is the oposite of the square they cancel each other out right? Then why bother in doing the calculations if they cancel each other out?
((-8)^^2)^^.5 )= (-8)^^1 = -8 . The fundamental error is an analysis problem. You started this problem with a statement: you knew the initial number were -8. If I agree with your argument that you must start with internal resolution, all algebraic equation solution in incorrect.
( − 8 ) 2 = 6 4 . 6 4 = 8 .
Note: In general, for any real number x , x 2 = ∣ x ∣ . We should also keep in mind that for x > 0 , ( − x ) 2 = ( − x ) 2 . This is because the first radical takes the form of an imaginary number, which is a whole other thing to cover.
should'nt the answer be -8 and +8, as : sqrt(x^2)=lxl=+xand-x here , sqrt((-8)^2)=l-8l=-8 and 8
Log in to reply
yes, for Pete's sake; the square root of any positive number has two solutions, a positive and a negative, Isn't minus eight time minus eight 64? This is level one algebra. Surprised "Brilliant" aint so brilliant here.
It is not true that ∣ x ∣ = ± x . The absolute value function only returns one value, and not two values.
Log in to reply
Surely this would simplify to (-8)^(2/2) = (-8)^1=-8? "To raise an expression to the nth index, copy the base and multiply the indices."
how you will prove it?
Yes, it should be.
No, because conventionally the square root sign will only give the positive answer. In other words, if x^2=4 is the equation in question, then the solutions would be +2 or -2, as x^2 - 4 = 0 can be factored into (x-2)(x+2) = 0. But if we have x=sqrt(4), then the answer will only be two, as the conventional definition of the square root sign means that it has a non-negative range.
No, thats noy true
Square root sign usually implies positive root only. When we write sqrt(3) we would ussume it to mean the positive root. Same thing here. If we squared the above expression, and then said that was equal to x squared, and then were asked to find the value of x, then there would be 2 solutions.
No, +sqrt(64) is +8, -sqrt(64) = -8. But the question asked +sqrt(64).
I always had this question: Why is
(
x
2
)
=
∣
x
∣
because using exponential rules :
(
a
m
)
n
=
a
m
∗
n
given radical can be
thought as
(
−
x
)
(
2
∗
1
/
2
)
=
−
x
Log in to reply
I did this too!
Log in to reply
After some consideration, I agree that the answer is 8. I say this because -8^2 = 8^2 , so to remain continuous the sqrt of -8^2 would have to equal the sqrt 8^2 as well as the answer. Certainly the sqrt of 8^2 doesn't equal -8, so -8 is not a solution leaving only positive 8.
Log in to reply
@Joe Hillman – the answer is +8 and -8 if we talk about geometry or other branches of math which deals with dimensions and etc.. but when we talk about algebra, the answer is simply +8...
Yeah that's what i did as well!
Log in to reply
@Joe Hillman What does (-8)^2 = 8^2 have to do with continuity? There is no logical explanation of that!
yes you true.
If we have: sqrt((-8)^2) = ((-8)^2)^(1/2)=(-8)^(2*1/2)=-8 this is the correct answer
Log in to reply
the answer is +8 and -8 if we talk about geometry or other branches of math which deals with dimensions and etc.. but when we talk about algebra, the answer is simply +8...
i got confused, the square root and square cancelled out each other
sqrt(x^2) = |x| means, it is -x when x<0 and +x when x>0. So the answer should be -8
Log in to reply
You are almost right, I want to correct just one thing, the answer is |x|, not x hence the answer is 8 not -8, |8|=|-8|=8
-8 will be the answer if there is a negative sign before the square root..
It should be -8,
√(-8)² = √ { (-1) (8) }² = √ ( 8 i² )² = 8 i² = 8 x (-1) = -8
Log in to reply
please excuse my dear aunt sally, parenthesis first (-8)^2 =-8x-8 =+64 then exponents or roots so sq rt of +64 is +8 am I wrong?
Log in to reply
@Charlie Rosales – No, actually I'm wrong, but the reason you gave is correct, but incomplete too :-) I mean there are more reasons for it to be + - 8.
@Charlie Rosales – See 8 multiply8=64 Similarly,-8multiply-8=64 So we can say square root of any positive no gives 2 value , they are one positive and other negative
I agree with the proof of Jyo Moy the exact answer is -8 because sqrt(xy) is defined in R iff either x is non-negative or y is non-negative. Therefore we use complex number to handle this type of problems.
Should this br positive or negative 8 ?
PEMDAS right?
Log in to reply
With Pemdas, and parenthesis you work from the inside out right?
-8^2*1/2= -8^1=-8,why this is not correct.if it is written in exponential form.
it can also be written as exponent 1/2 and 2 and 1/2 when canceled leave us with -8 hence -8 can also be the answer.
Log in to reply
That's the thing. You do not cancel out functions. That is a fundamental rule in mathematics. You have to compute the function and then use that value to feed the other function. You cannot cancel it out unless they are direct inverse functions of each other, like e power, and log(e).
Log in to reply
okay thank you for the clarification
Log in to reply
@Gayatri Petrova – We can also right√ 8i * 8i = √64 * -1 = -8 , what I hv learned is that whenever there is imaginary no first convert it into real and then take square root
I still believe, the given radical when simplified/rewritten according to law of exponents, does give answer of -8. @Calvin Lin : Can you please elaborate?
I agree with you. Maybe both answers are right...
You would still work from the inside out. So, the notation would look like ((-8)^2)^(1/2 )
shouldn't the answer be pos. or neg. 8 but since you already mentioned that the x is a negative no. therefore the positive no. is neglected ??!
U r absolutely correct.
The answer is definitely -8 and 8 because the square root of any number X is plus and minus the root of X as if you square the negative root or the positive root you get X. That is what all of my A level teachers and exams say.
Ya your note is rt, but one thing I need to say square of any no is always positive ,but square root of any no is always positive and negative,what u say
Let's try this on for size. Let's say that this is a complex number. The complex numbers are a field. Multiplication in a field is commutative. sqrt((-8)^2)=sqrt((-8) (-8))=sqrt(-8) sqrt(-8)=sqrt((-1) (8)) sqrt((-1) (8))=sqrt(-1) sqrt(8) sqrt(-1) sqrt(8)=-1*8=-8. Order of operations broken down into field operations instead of "which operation goes first".
Log in to reply
This is an excellent explanation for why it must be -8.
Sqrt(64) is conventionally 8.. but then again, it could be both, and I am sure that you are familiar with the thing where sqrt(x^2) is taken to be +/- x .. However if you really want the answer to not be ambiguous you might as well say it is -8 instead of 8.. cause come on man, in the expression you clearly squared it first before taking its root.
The sq. root of any number has two solutions.. it's a many-one function. In this case, its clear that the solution is -8. Consider it this way. The square function is the inverse of sq. root so they nullify each other leaving the answer as -8...
too logic. right
I think the most general answer is plus or minus 8...if you start with the function f(x)=x^2 then sqrt(f(x))=plus or minus (f(x))^(1/2) which = plus or minus x, and not |x|. If you only consider |x| you just lost a solution...In an actual model however the answer depends on context either solution could be correct depending on how your model work
actually square root 64 is either 8 or -8
It should be -8,
√(-8)² = √ { (-1) (8) }² = √ ( 8 i² )² = 8 i² = 8 x (-1) = -8
Log in to reply
So, which is the final reason for solution?
Log in to reply
The answer should be -8 and 8, since the square root of 64 is +-8.
shouldn't it be -8 because doesn't the square and the square root cancel each other out?
As x 2 = ∣ x ∣
( − 8 ) 2 → ∣ − 8 ∣ → 8
The answers session is getting worse each time. People are so arrogant and can't they admit that they are wrong. The answer is 8. Period. This is a Level 1 question. If you don't understand, go back to the material and stop trying to push your non sense.
I tend to agree with this comment.
you sound pretty arrogant yourself. I'm just as certain the answer is +-8 (plus OR minus 8). -8 squared is 64, just as +8 squared is 64. I'm probably giving up on this site if it cannot give a clear rational for its supposed correct answer.
Log in to reply
Yes, you should give up. The answer is not +-8. The answer is +8.
Log in to reply
then simply tell me what is negative 8 squared? Same answer as positive 8 squared.
Log in to reply
@Giacomo Re – Omg. If they're the same (both are 64), how can the square root be different? The question is what's the square root of 64. It's 8. Not -8.
( 8 ) 2 = ( − 8 ) 2 = 8
Log in to reply
@Renan Silva – If the question was: Compute x in x 2 = 8 , then the answert would be +8 or -8.
the clear, rational answer is simply that you must simplify the equation within the square root symbol before you can apply the square root to said simplified equation ... as such, the simplification of (-8)(-8) is +64. When you then apply the square root to the simplified equation, the square root of +64 is always and unequivocally +8, not +/- 8
Ok. How about this then. The answer is 8 because you can only pick one answer. The Convention Agreement
Log in to reply
It's not picking one answer. This is how the root square function is defined. The range of this function is all non negative real numbers. Do you know the concept of a function range?
Log in to reply
@Renan Silva – I know hun. ..im a nurse... some times in life all answers are correct and you have to use critical thinking to decifer the best answer..not the right one!!#
Log in to reply
@Laura Venterosa – People, it's the first lesson we tool in math, the square root of positive number is either negative or positive, 2 possible answers, 2 possible solutions. i.e. square root of 64 = +/-8 , it's simple. it never depend if 64 was actually -8 -8 or 8 8 giving a question with 2 possible answer is real stupid.
Log in to reply
@George Nasry – "square root of positive number is either negative or positive". No, it's not. Just look at the function's graph. It's a half parabola. The function's image is non negative real numbers.
all right; that's as close to an excuse as I've come across here, but it's still not much of an excuse. How recent is this convention? It never was in all the years of math and engineering that I studied. In high school, I would certainly been marked wrong if I left out -8 as part of the solution.
Log in to reply
@Giacomo Re – if your high school mathematics instructors would have marked you wrong for not providing an incorrect answer, then I am GREATLY concerned about the credentials of said instructors, and even more alarmed by the current state of the educational system. The question asks you first to calculate (-8)(-8), and then find the square root of that answer ... (-8)(-8) is ALWAYS +64, and the square root of +64 is ALWAYS +8.
... of course, maybe Dr. Sheldon Cooper could invent 29 other alternate dimensions to make the math come out as +/- 8, but until said fictional character manages to produce such an answer, the answer to this question is and always will be simply +8
Log in to reply
@Steve Peters – Guys, let me simplify that to you. if you have the following equation ( X + 8) * ( X - 8 ) = 0 calculate the value of X? Oh, I remember these type of equation from 6th grade
Log in to reply
@George Nasry – George, let me simplify to you. That's not the question asked! The question is simply 6 4 . The answer is only 8 .
Log in to reply
@Renan Silva – Renan, I think your reply was directed for George (?) ... the root of 64 and the answer being only 8 is what I've been saying all along ...
Log in to reply
@Steve Peters – My mistake. I already changed the name.
The answer is plus or minus 8 not just plus 8
Wrong. -8 squared = +64, and the square root of +64 = 8
following the order of operations: BEDMAS
you must apply the squared value of -8 first, therefore (-8)(-8), which equals 64. you then calculate the square root of 64, which is 8.
the square and square root are not included in BEDMAS
Log in to reply
ummm hello? the Square is the EXPONENT in BEDMAS, and BEDMAS must be applied to the entire equation WITHIN the square root symbol before the square root can be calculated
Gosh..... sqrt(64) = 8 or -8
Hello. Just have to follow PEMDAS Rule by the way...you need to change the radical sign into rational exponent and then evaluate by following such rule...Prejudice is ignorance.
Note here that the square root only returns positive real numbers. In order to return both negative and positive real numbers, the ± symbol must be used in front of the √ symbol. So the answer will be 8.
minus 8 squared is Positive 64, the square root of which is 8.I am unsure why -8 is not also a valid answer though....
( − a ) 2 = ∣ a ∣
So ∣ − 8 ∣ = 8
The answer to this is +/- 8, there actually 2 answers. Any time you have a quadratic, there are always 2 answers. 64^1/2 is true for both 8 and -8.
Here are the order of operations:
PEMDAS
Parenthesis Exponents Multiplication Division Addition Subtraction
Using the order of operations:
(-8)^2 = 64, not -64. If the answer was -64, the equation would have to be -(8)^2 = -64.
The square root of 64 is 8. So, the answer to the question is 8.
-8^2 = + 64, Therefore Square root of 64 = -8 or +8, Then the answer is 8
Why can't -8 also be an answer? The sq rt of 64 is ±8 surely.
Expression in parenthesis are resolved first, so we follow the steps below.
Step 1:
Then step 2:
So 8 is the answer!
x^2 = 64 |x|=8 x=+8 or -8 sqrt(64)
8 is not a Proper Solution. The solution will be 8 and -8 both. Because Squire Root of any positive number always have 2 roots.
Yes, this is what I thought. I can see when you limit the range or a y=sqrt(x) graph you will only have one result. Yet this question does not suggest you need to use the functions or that the range was limited for either. This means you would have two values. Then following the order of operations means it is square rooted last, hence still providing 8 or -8.
If anyone has a valid response to provide the answer 8. I would love to hear it as I do need to know this for upcoming exams, this also meant I revised the facts above before posting this.
(-8)^2 = 64 ... then sqrt(64) = 8 :D
Obviously, For any x real number, x 2 = ∣ x ∣ . So, ( − 8 ) 2 = ∣ − 8 ∣ = 8 .
Sqrt((-8)^2= 8. This is because the exponent is outside of the parentheses of (-8) meaning that it would be -8 x-8 which is equal to 64, sqrt64=8 had the question been sqrt(-8^2) it would simplify to -64, sqrt-64= -8
Clearly my simple math is different. I wish I could keep up with all those technical answers. Anyone else just stick with the simple order of operations and 3rd grade multiplication of negatives? (-8)(-8)=64 Square root of 64 is 8
your simple explanation is all that is required here Laura :)
what is negative 8 squared? What is negative 8 times negative 8? They're both 64.
good grief, the square root of any positive number has two solutions, a positive and a negative.
Log in to reply
"the square root of any positive number has two solutions" Good grief, you don't know basic math.
the answer is +8 and -8 if we talk about geometry or other branches of math which deals with dimensions and etc.. but when we talk about algebra, the answer is simply +8...
the answer is positive and negative 8..
Ok. How about this then. The answer is 8 because you can only pick one answer. The Convention Agreement.
(-8X-8 = +64) so square root of 64 is 8
sqrt of (-8)^2 = (-8)^2 x 1/2 = -8
(-8)×(-8)=64 root of 64 = 8 answer.
its simple that answer is 8 cause (-) is inside the bracket and also surrounded by a squire if we want to write it like -1*(8) its a wrong approach. here first of all we must vanish the squire then further operation ..
Using the rules of indices, we could get
(-8)^2/2 Therefore, -8 is also a solution.
Using the manual method, we could get sqrt(64) which is -8 or 8 therefore 8 is also a solution
in algebra sqrt(x^2)=|x|=|-8|=|8|=8
so now what
I believe there are two answers to this question, both 8 and -8. Why I say this is because you can cross out the square root with the square (2) (The crossing out can only be done if its powered by two just like this question, I forgot why coz I didn't do math for awhile) and you are left with -8 (1st answer) and I said 8 is the answer too because (-8)2=64 and the square root of 64 is 8. Please correct me if I'm wrong. Thanks.
Log in to reply
because the square occurs within the value of the the square root, you must calculate everything within the root symbol before you can calculate the square root itself. following the order of operations, you have a value of 64 within the square root symbol [-8 x -8 = 64]. Once you have calculated that value, you get an equation asking for the square root of (-8)(-8). As (-8)(-8) = 64, the square root is therefore 8.
Log in to reply
Okay. Thanks
{(-8)^2}1/2 =(-8) ans=(-8)
Log in to reply
@Priyanka Saini – Sorry, but no. the order of operations applies to everything within the square root symbol in order to simplify the problem, which means you must calculate its total value BEFORE calculating square root.
the only way to come to an answer of -8 for this problem would be if you were squaring the entire equation, but that is not what is asked.
if I asked "what is (-8) squared?" the answer would be +64 if I asked "what is the square root of +64?", the answer would be +8
Therefore, when the question asks "what is the square root of an equation that has an answer of +64?"...
the answer is +8 ... not +/- 8 ... not -8 ... simply 8
Log in to reply
@Steve Peters – Guys, lets replace the "-8" by "x". And lets say that "x" is a real number. Now you are telling me that sqrt(x^2) is not equal to x?
Log in to reply
@Claudio Flores – your suggestion alters the entire original question
@Claudio Flores – sqrt(x^2) equal to |x|
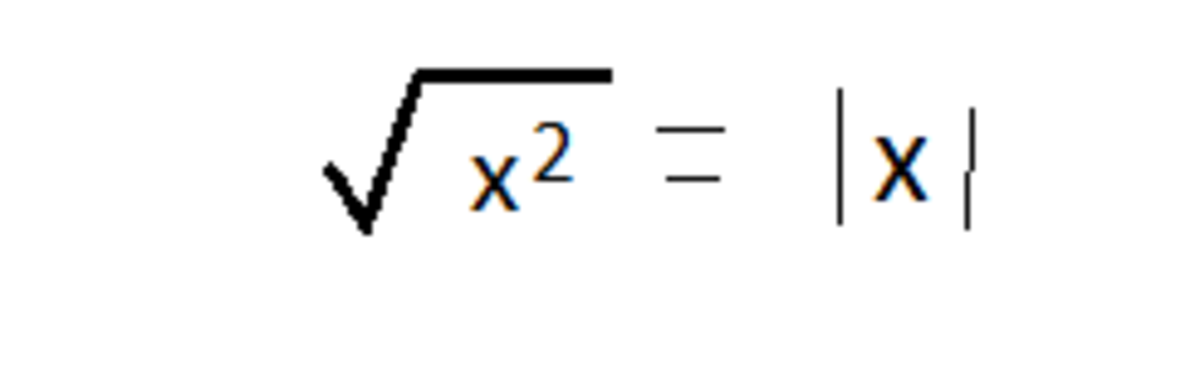
Expression in brackets are resolved first, so we follow the steps below.
Step 1:
( − 8 ) 2 = 6 4 .
Then step 2:
6 4 = 8 .
So 8 is the answer!