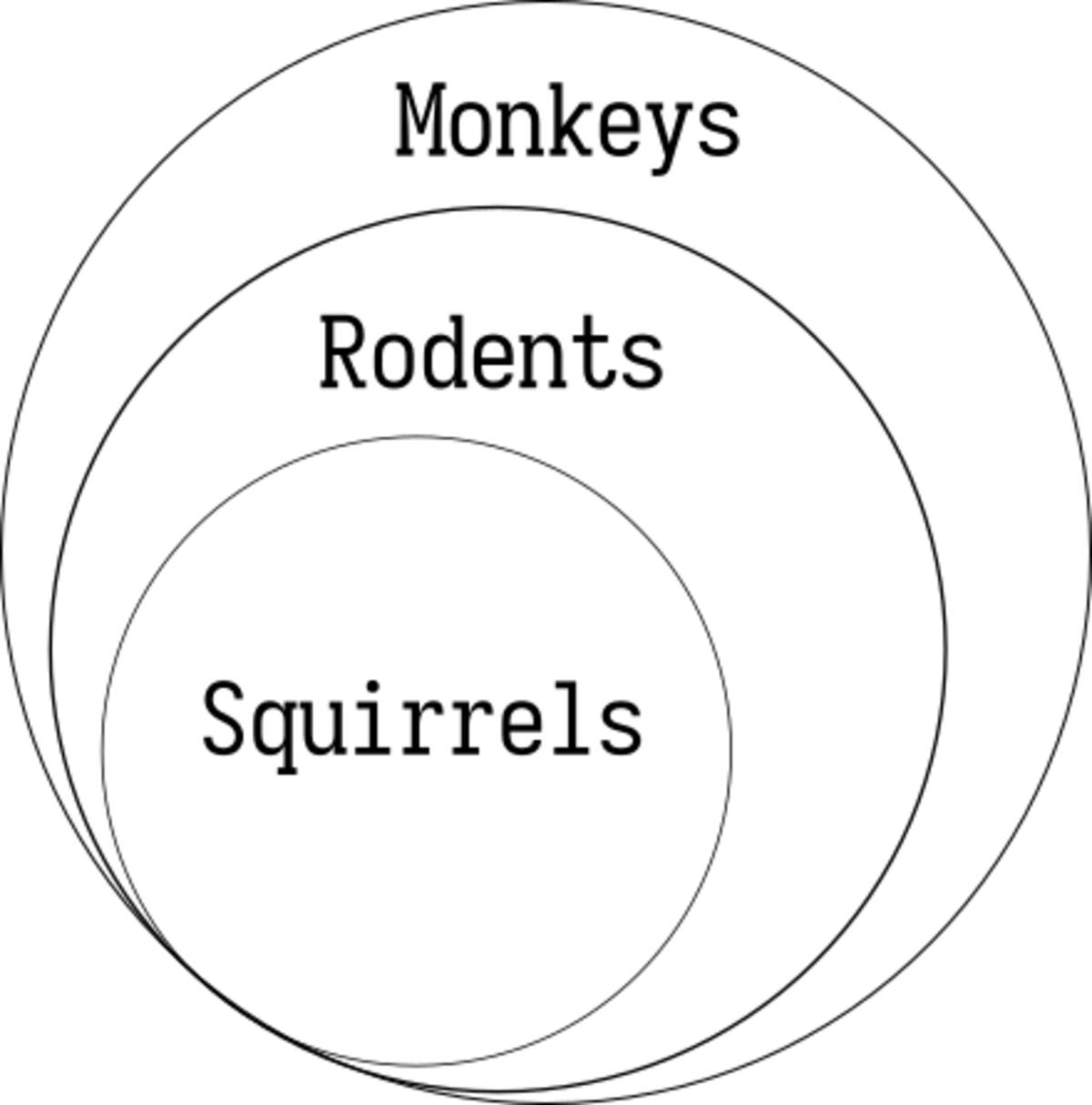
All monkeys are squirrels? (Mathathon Problem 2)
You know the following -
- All squirrels are rodents.
- All rodents are monkeys
So from this information, can you say that all monkeys are squirrels?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
19 solutions

| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | The gif is very smooth and clear |
| Ingenuity | 2/5 | Venn diagrams and set theory used, but not explained much |
| Total | 12/15 | Great job! I will update your score on the members and points note! |
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | You are an expert of moving images in a loop which continue to x where x = y ➝ 0 lim y 1 ! |
| Ingenuity | 2/5 | Self explanatory Venn diagrams with beautiful pictures |
| Total | 12/15 | Great job! Percy might update your score on the members and points note! |
Log in to reply
I AM a gif expert! lol But each time I have to redo them from the start because my first draft is usually >> 10Mo...
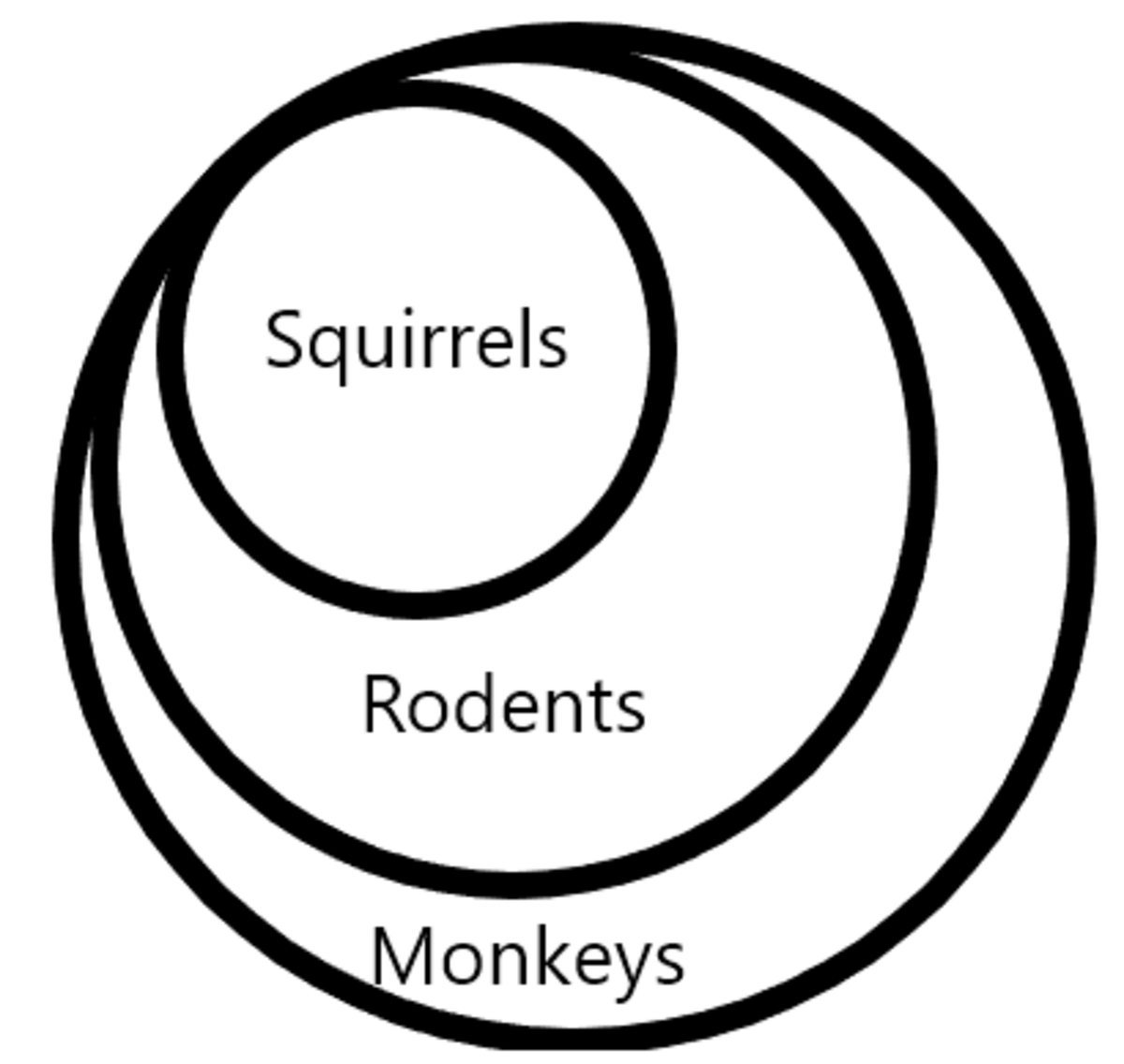
First, let's formulate these statements. If S is the set of all squirrels, M is the set of all monkeys, R is the set of all rodents and a is an animal that could be in any one of those sets, we get a ∈ S a ∈ R ⟹ a ∈ R ⟹ a ∈ M . From which we can immediately conclude that a ∈ S ⟹ a ∈ M . So every squirrel has to be a monkey. Note though, that these are implications, not equivalences. If they were equivalences (meaning a ∈ S ⟹ a ∈ M ∧ a ∈ M ⟹ a ∈ S ), then we could conclude that all monkeys are squirrels. Look at this Venn-Diagram to see what I mean:
You can immediately see that there are monkeys that are neither squirrel nor rodent.
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Proper latex has been used and venn diagram makes it simpler |
| Ingenuity | 5/5 | Set theory, set notation and the venn diagram blended nicely |
| Total | 15/15 | Mind-blowing performance! I will update your score on the members and points note! |
Nice solution! I misread the problem :(
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Answer flows like honey (we are not gonna have an argument over that again Percy) |
| Ingenuity | 5/5 | Set theory and the Venn diagram are perfectly used |
| Total | 15/15 | Marvellous! Percy might update your score on the members and points note! |
Log in to reply
Ok, flows like honey, not gonna argue :)
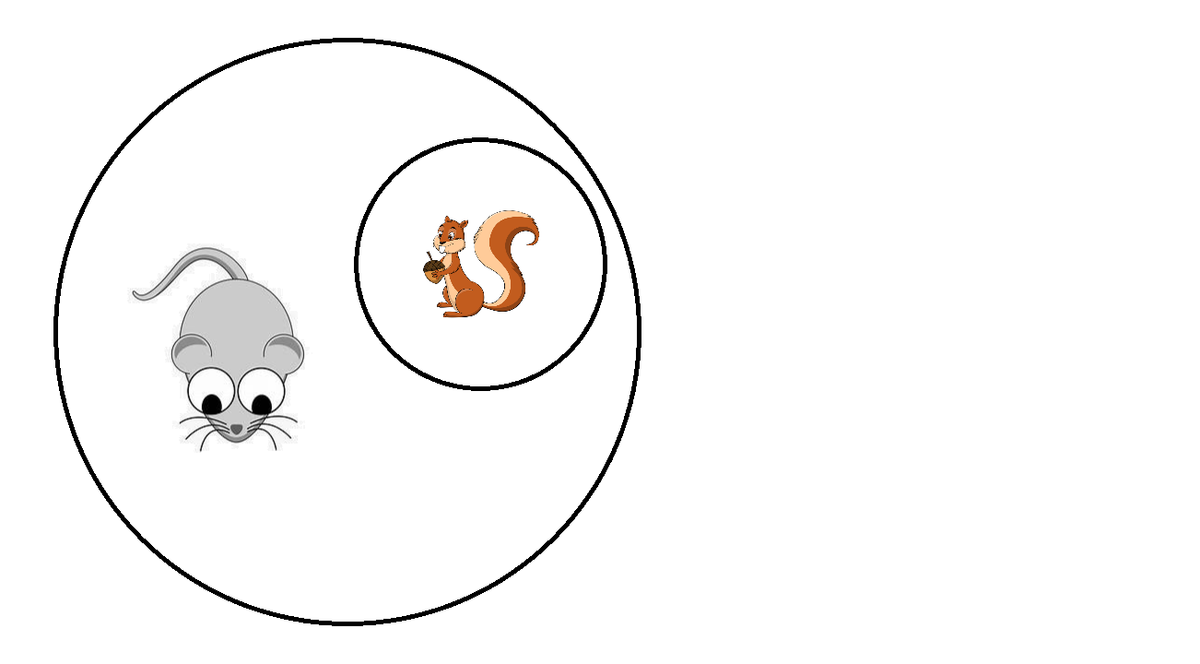
All squirrels are rodents
⇒
Squirrels ∈ Rodents
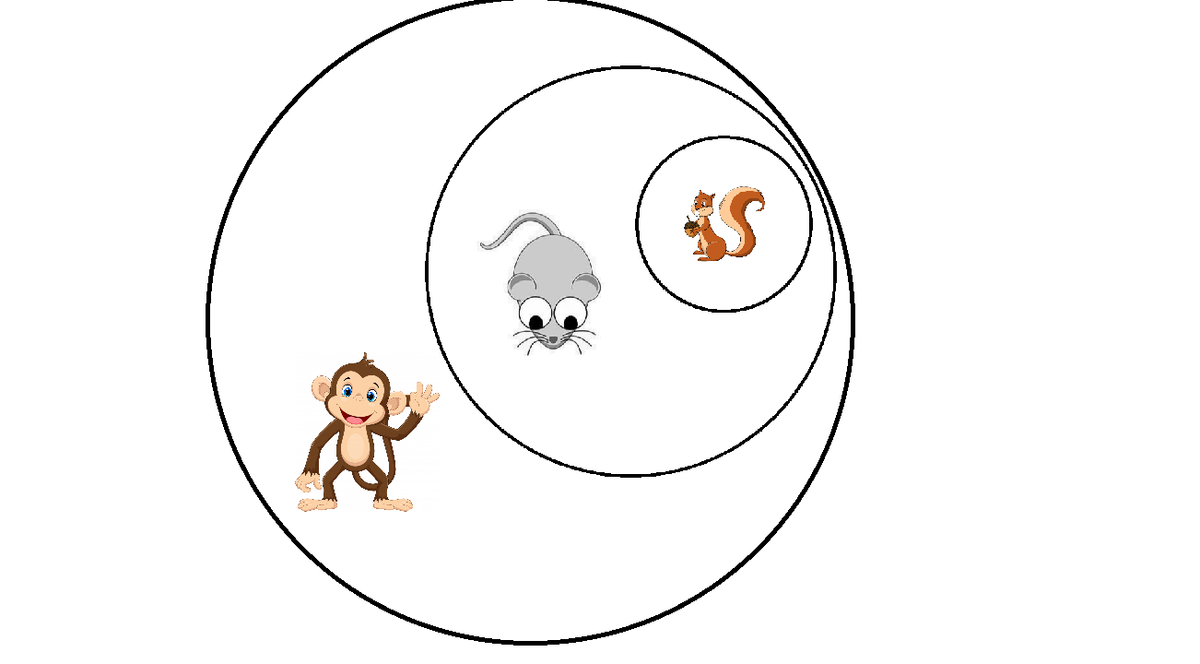
All rodents are monkeys
⇒
Rodents ∈ Monkeys
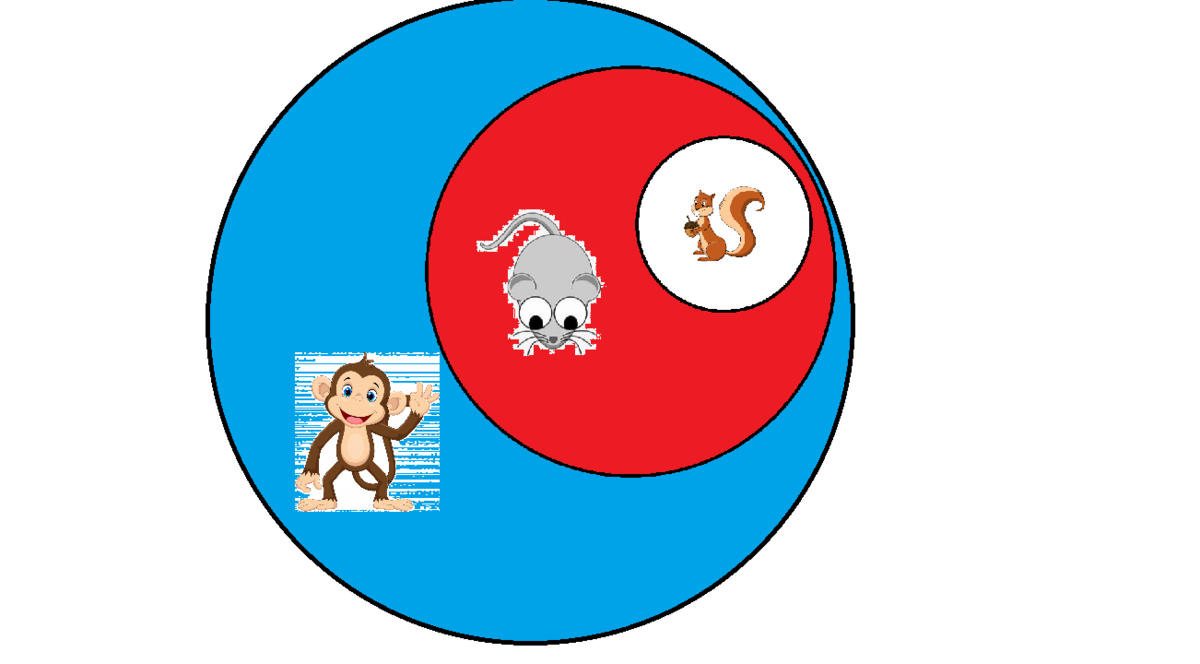
Hence, the answer is
No
, since the monkeys in the red-and-blue area aren’t squirrels, and the ones in blue aren’t even rodents.
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Everything is clear and readable |
| Ingenuity | 3/5 | Diagrams, set theories, good |
| Total | 13/15 | Great job! I'm sorry about my vagueness but I'm running out of things to say! |
Log in to reply
Yeah you forgot how to add too
Percy Jackson
| Accuracy | 0/5 | 5+5+3=13≠10 |
| Readability | 5/5 | Table format |
| Ingenuity | 0/5 | Same approach |
| Total | 5/15 | Its fine... |
Log in to reply
lol I was in hurry, copy pasted but forgot to change the 10
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Everything is clear and readable |
| Ingenuity | 2/5 | Nice diagrams |
| Total | 12/15 | Great job! I'm sorry about my copyness but I’m running out of things to say |
This is a classic syllogism where , through transitivity, All p's are q's and All q's are r's can be combined into All p's are r's. In this case, this leads to : All p's are r's. But this does not imply the converse, that is all monkeys are squirrels. In fact, even the converse of the second statement is not true in general, i.e. All monkeys are rodents is not true in general. It is true that some monkeys are rodents and some rodents are squirrels but they may be disjoint sets.
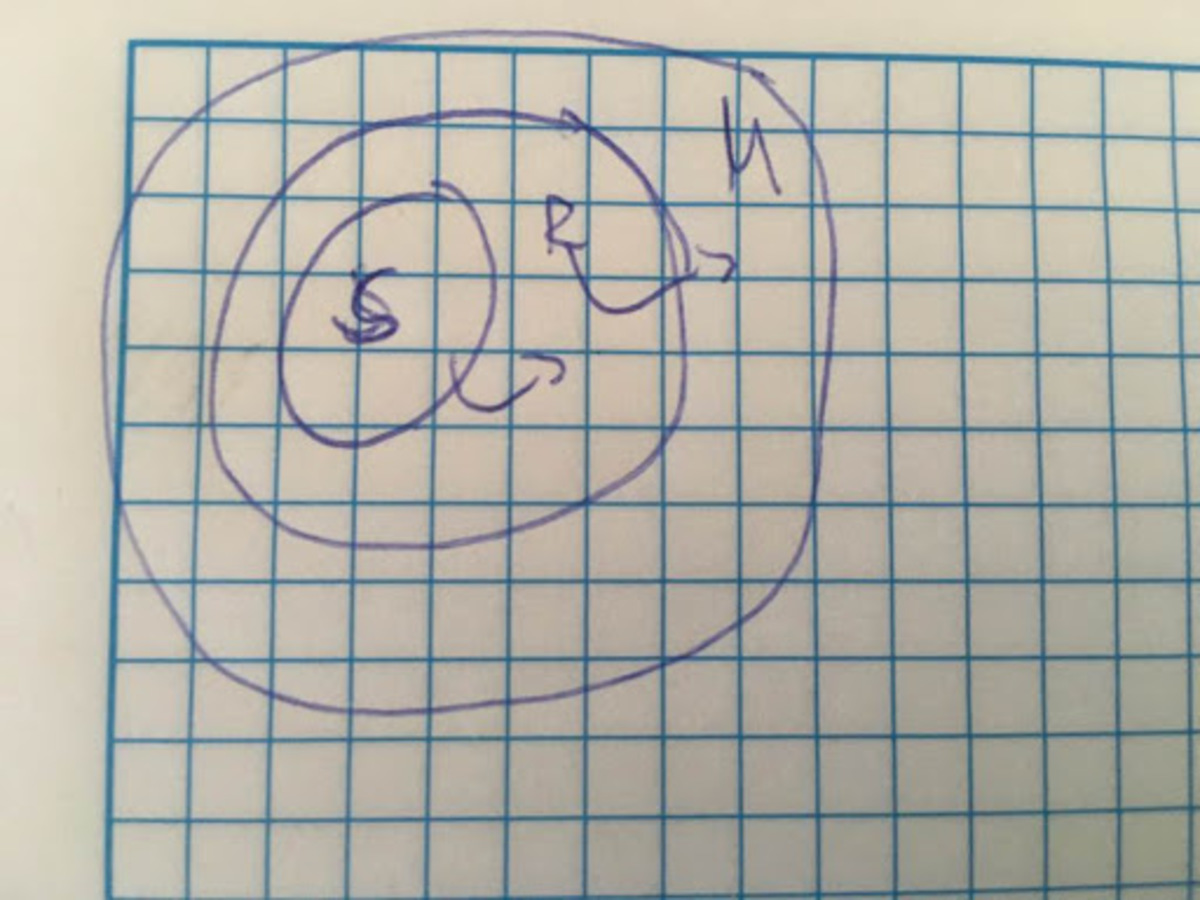
Let's call the set of squirrels
S
, the set of rodents
R
, and the set of monkeys
M
.
From the problem, we have
S
∈
R
, and
R
∈
M
. From this, we can construct a Venn diagram;
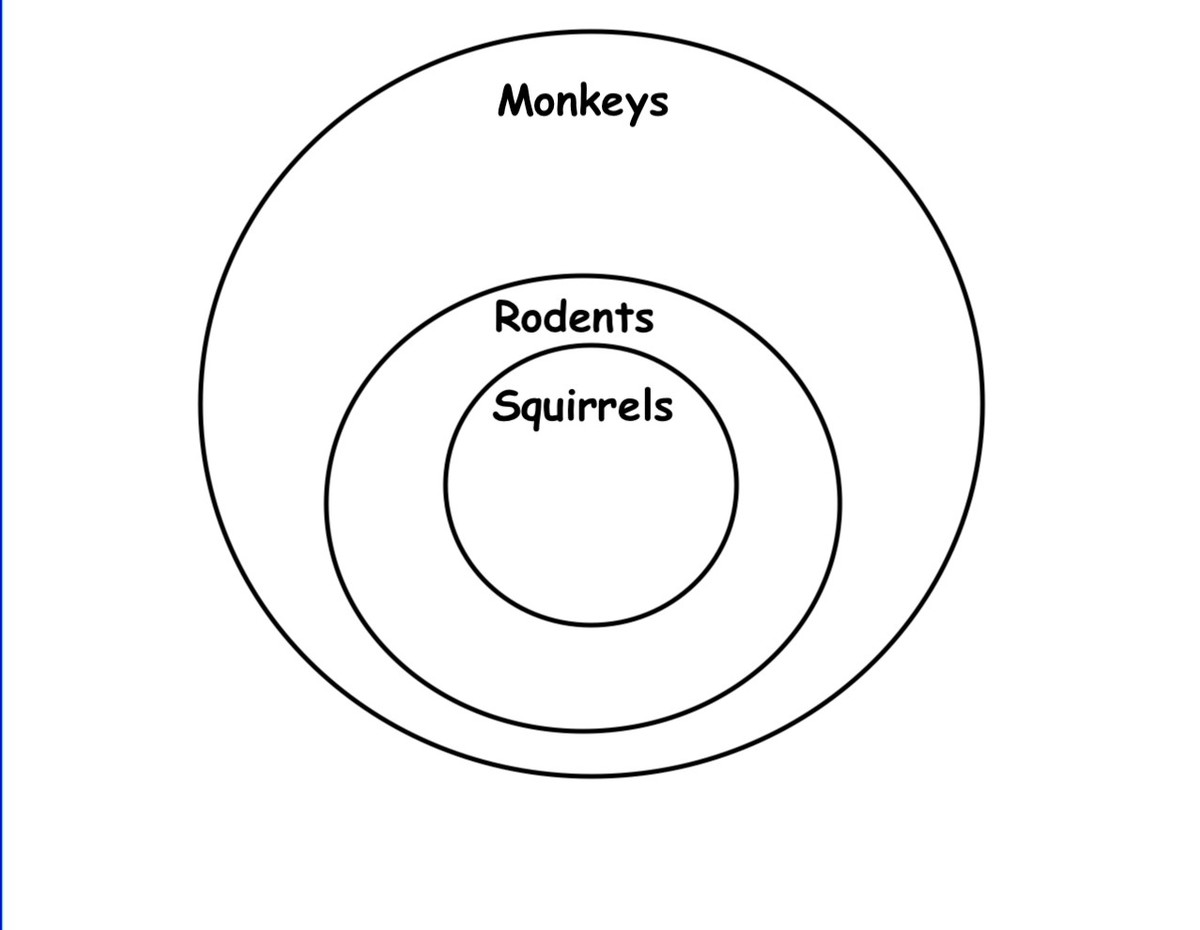 I can leave a space between the circles because the problem didn't state that all rodents are squirrels, and that all monkeys are rodent. From the Venn diagram, we can easily see that there is some space between the rodent's circle and the monkey's circle, which must mean that there is some creature that is a monkey, but not a rodent or a squirrel, so therefore, the answer is
N
o
I can leave a space between the circles because the problem didn't state that all rodents are squirrels, and that all monkeys are rodent. From the Venn diagram, we can easily see that there is some space between the rodent's circle and the monkey's circle, which must mean that there is some creature that is a monkey, but not a rodent or a squirrel, so therefore, the answer is
N
o
Sorry for the blue line
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Everything is clear and readable |
| Ingenuity | 3/5 | Nice blue line, Percy will love it(You explained why you can leave a space clearly) |
| Total | 13/15 | Great job! Add red lines too next time (my fav colour is red) |
Let
S
,
R
,
M
notate the set for squirrels, rodents and monkeys. Then we have
S
∈
R
,
R
∈
M
.
∴
S
∈
M
.
I can therefore conclude all squirrels are monkeys (what?!).
But the question asks whether all monkeys are squirrels, which is whether
M
∈
S
.
Since we have
S
∈
M
already, either
M
∈
S
is true and
M
=
S
or
M
∈
S
is false and
M
=
S
.
We cannot be sure, so the answer is NO.
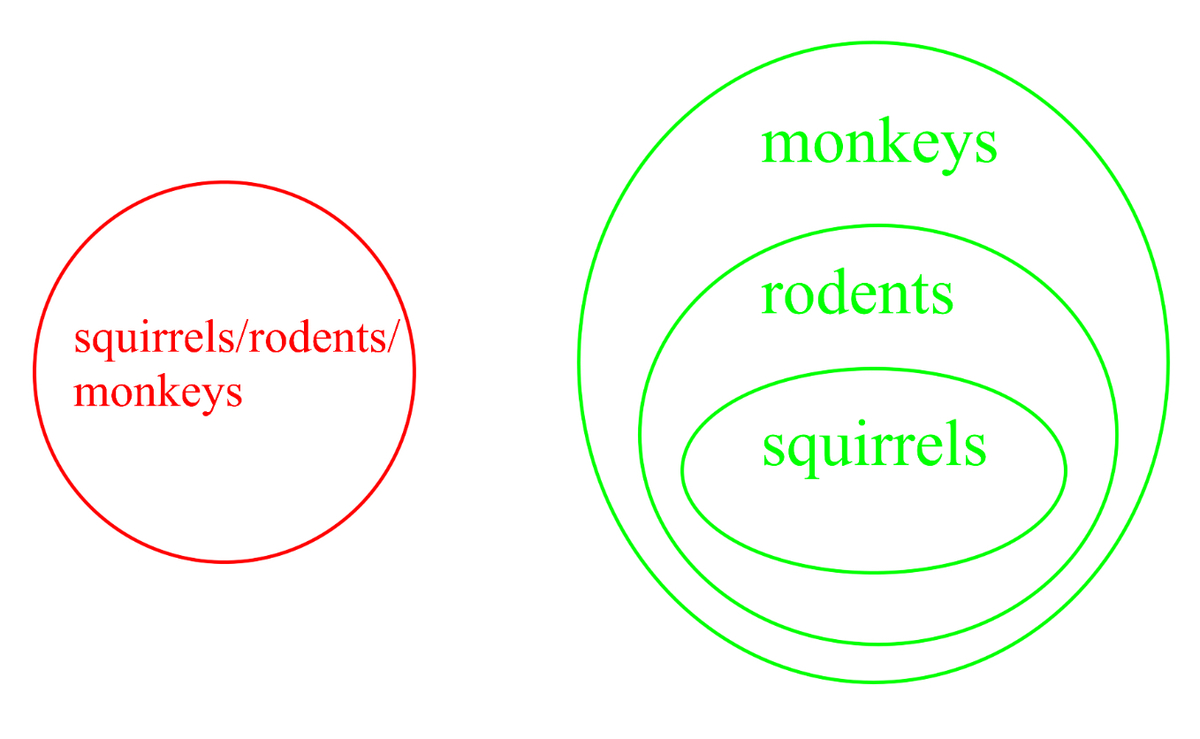
This Venn diagram may help :)
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Everything is clear and readable |
| Ingenuity | 2/5 | Nice diagrams, extra marks for the ellipse used kidding |
| Total | 12/15 | Great job! |
Terminologies in Set Theory
Elements : Objects belonging to a set
Subset : If all elements from a set (say A) are also element of another set (say B), then A is subset of B. It is denoted as
A ⊆ B
-
All S q u i r r e l s are R o d e n t s . From this we can conclude that the set of all S q u i r r e l s is a subset of the set of all R o d e n t s i.e. S q u i r r e l s ⊆ R o d e n t s .
-
All R o d e n t s are M o n k e y s . From this we can conclude that the set of all R o d e n t s is a subset of the set of all M o n k e y s i.e. R o d e n t s ⊆ M o n k e y s .
Conclusion
S
q
u
i
r
r
e
l
s
⊆
R
o
d
e
n
t
s
⊆
M
o
n
k
e
y
s
(this is represented by the Venn Diagram).
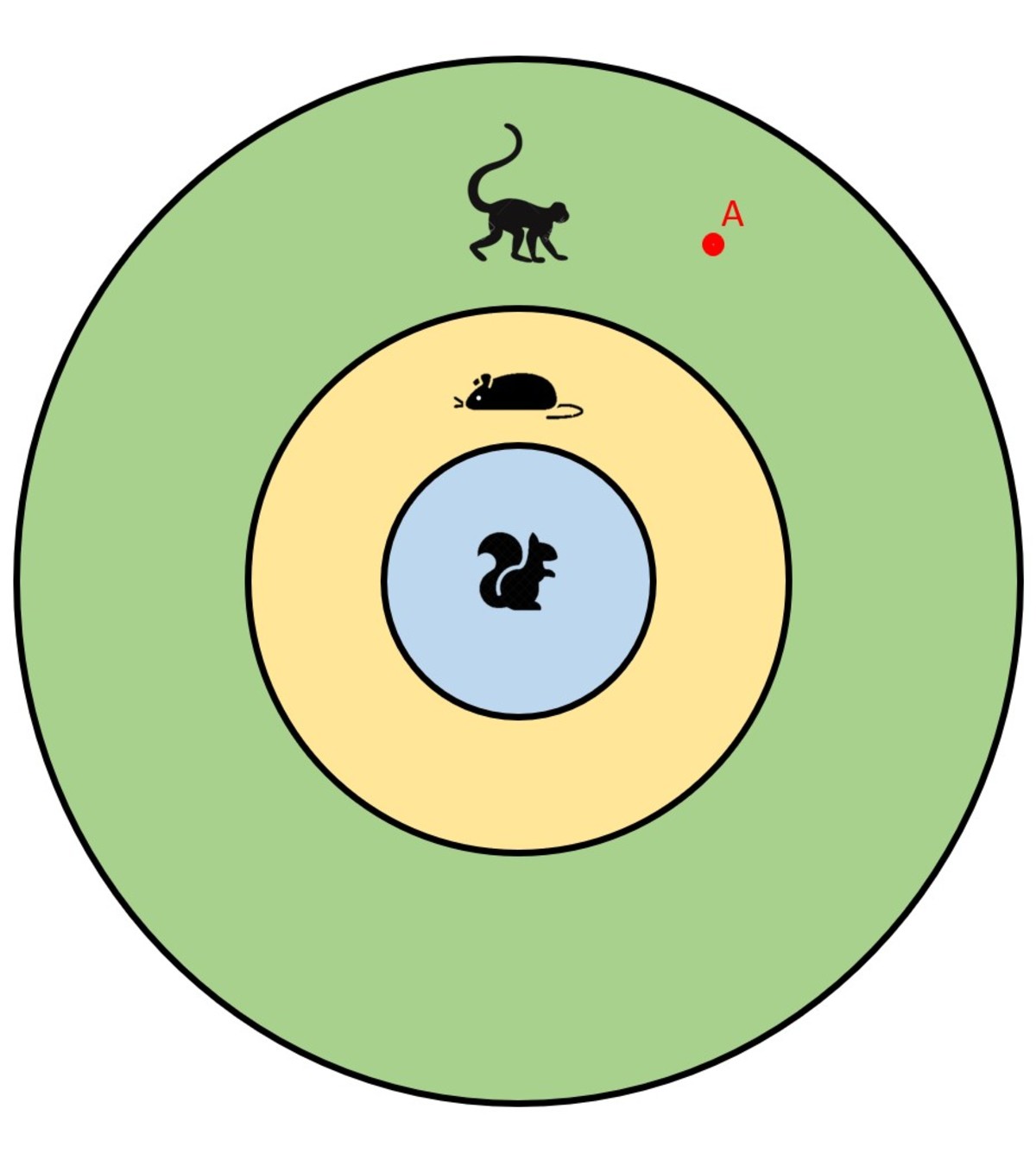
From this it is clear that, with given information, though all S q u i r r e l s are M o n k e y s , all M o n k e y s are not S q u i r r e l s . (Considering all sets are not equal)
E.g. M o n k e y represented by point A on Venn Diagram is not a S q u i r r e l .
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Everything is clear and readable |
| Ingenuity | 4/5 | Set theory explained well and diagram given |
| Total | 14/15 | Great job! I will update your score on the members and points note! |
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Everything is clear and readable |
| Ingenuity | 4/5 | Set theory has been explained well |
| Total | 14/15 | Great job! I'm sorry about my copyness but I’m running out of things to say |
First let's look at an analogy:
-
All Natural Numbers(N) are Whole Numbers(W). This does not mean that all whole numbers are natural numbers. For example, 0 is a whole number but not a natural number.
-
All Whole Numbers(W) are Integers(Z). Similarly all negative integers are not whole numbers.
So, all natural numbers are integers but all integers are not natural numbers(-2,-4,0 etc.)
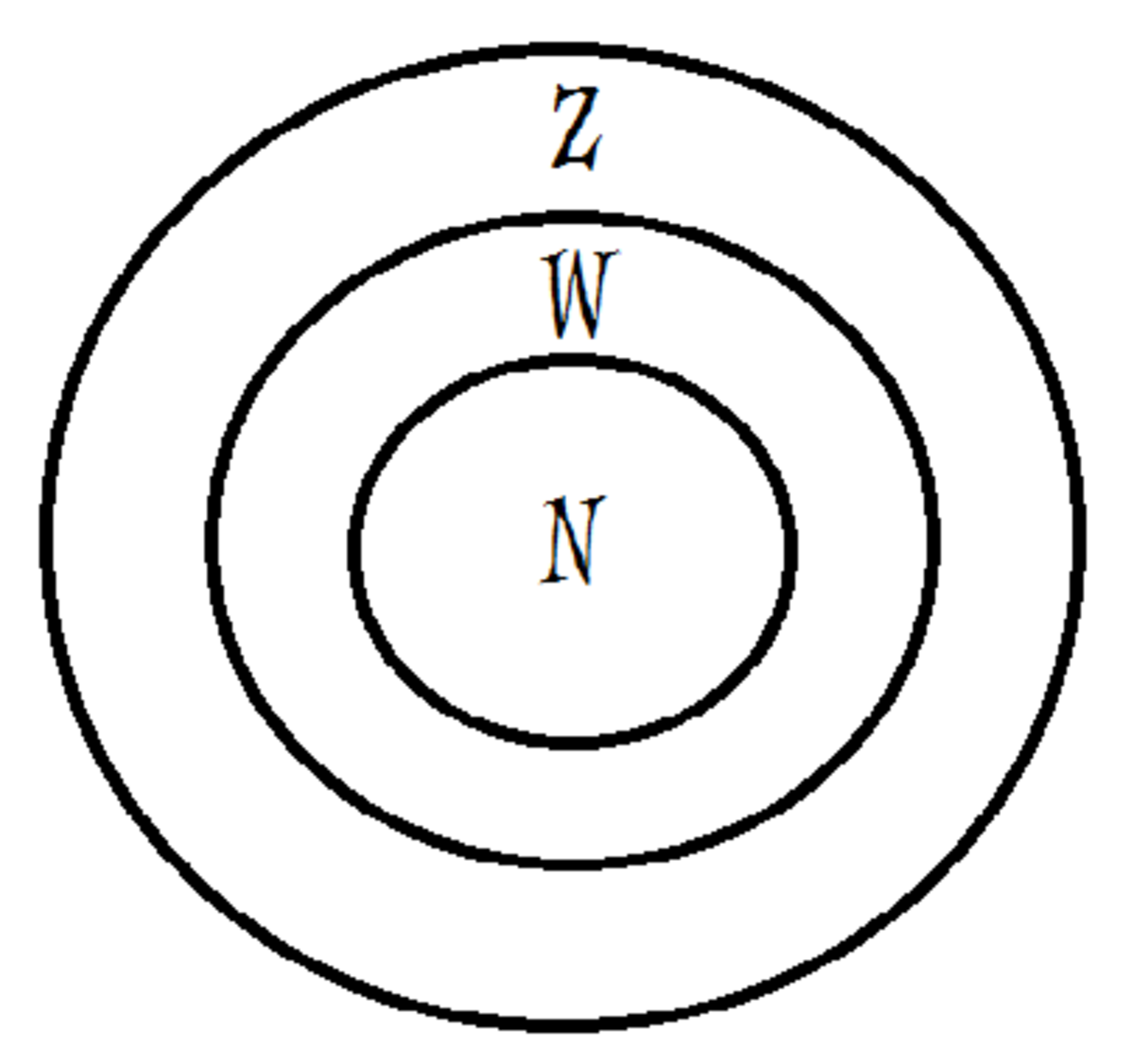 Venn diagram representation
Venn diagram representation
Similarly, we infer from the information given that all squirrels are monkeys, but monkeys are not squirrels.
 all monkeys are
not
squirrels
all monkeys are
not
squirrels
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Everything is clear and readable |
| Ingenuity | 4/5 | Good analogy of number theory and venn digrams given |
| Total | 14/15 | Great job! I will update your score on the members and points note! |
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Its clear, but not very easy to understand |
| Ingenuity | 3/5 | Nice use of analogy |
| Total | 13/15 | Great job! Percy might update you score on the members and points note! (might) |
 Image
Since all squirrels are only part of the group of monkeys, and there are other monkeys which are not squirrels, the answer is
N
o
.
Image
Since all squirrels are only part of the group of monkeys, and there are other monkeys which are not squirrels, the answer is
N
o
.
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Everything is clear and readable |
| Ingenuity | 2/5 | Venn diagram |
| Total | 12/15 | Great job! I will update your score on the members and points note! |
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Very clear and only 30 wordish to read |
| Ingenuity | 3/5 | Concise but complete |
| Total | 13/15 | Great job! Percy will update your score on the members and points note! |
S = { x : x i s a s q u i r r e l } R = { x : x i s a r o d e n t } M = { x : x i s a m o n k e y } p : A l l s q u i r r e l s a r e r o d e n t s . q : A l l r o d e n t s a r e m o n k e y s p ⇒ S ⊆ R q ⇒ R ⊆ M ⇒ p a n d q ⇒ S ⊆ M ⇒ ( x ∈ M ⇒ x ∈ S ) ⇒ n o t a l l m o n k e y s a r e s q u i r r e l H e n c e t h e a n s w e r i s N O
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Everything is clear and readable |
| Ingenuity | 3/5 | Set theory used very well |
| Total | 13/15 | Great job! I will update your score on the members and points note! |
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Everything is clear and readable |
| Ingenuity | 3/5 | Set theory used very well |
| Total | 13/15 | Great job! I can’t update your score on the members and points note! |
First from set theory we can call all squirrels as rodents, and all rodents as monkeys. Now the population of rodents(includes squirrels) can't exceed the population of monkeys because rodents is subset of monkeys (A subset value never exceeds that of its set), a similar statement can be said for squirrels (subset) and rodents (set)
There will be 4 cases because there nothing mentioned about the population.
- When population of each animal is different.
- When only population of rodents and squirrels are equal.
- When all 3 have same population.
- When only population of rodents and monkeys are equal.
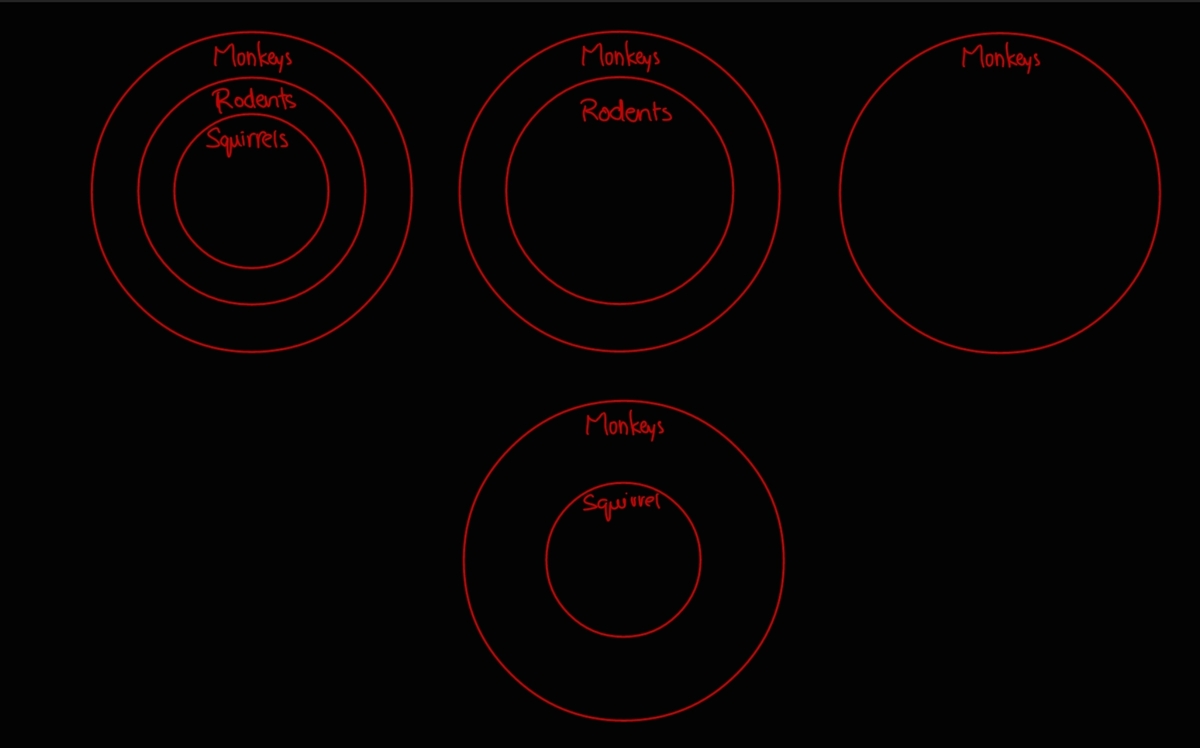 These are respective Venn Diagrams.
These are respective Venn Diagrams.
From the Venn diagrams, we can see that we can't necessarily tell that all monkeys are squirrels. Therefore ans is N o o o o o . . . . . . .
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Everything is clear and readable |
| Ingenuity | 4/5 | Venn diagram is used, and all possible cases are considered |
| Total | 14/15 | Great job! I will update your score on the members and points note! |
Log in to reply
@Percy Jackson there is small mistake 5+5+4 = 14 not 13
Log in to reply
Done, I was in a hurry, sorry
Log in to reply
@A Former Brilliant Member – Hey Percy I think I missed 1 case can I add that case in the solution
Log in to reply
@Omek K – Yes, but score will not be changed.
What about the case when only population of rodents and monkeys are equal? Is this impossible?
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Everything is clear and readable |
| Ingenuity | 2/5 | Nice case by case analysis |
| Total | 12/15 | Great job! I can’t update your score on the members and points note! |
Given S q u i r r e l s ⊂ r o d e n t s and r o d e n t s ⊂ m o n k e y s We can conclude that s q u i r r e l s ⊂ m o n k e y s because subset is a transitive relationship, but we can not conclude that m o n k e y s ⊂ s q u i r r e l s . Although the given statements do not rule out all three sets being exactly the same, we can not conclude that that is the case.
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Everything is clear and readable |
| Ingenuity | 3/5 | Set theory used |
| Total | 13/15 | Great job! I will update your score on the members and points note! |
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Everything is clear and readable |
| Ingenuity | 2/5 | Set theory used |
| Total | 12/15 | Great job! I will not update your score on the members and points note! |
All squirrels are rodents
This statement tells us that every squirrel is a rodent.
This does not necessarily mean that every rodent is a squirrel. Squirrels are only one of the things that are rodents. For example, all rats are rodents, and so are the squirrels. It doesn’t mean that squirrels are rats.
Here is the diagram:
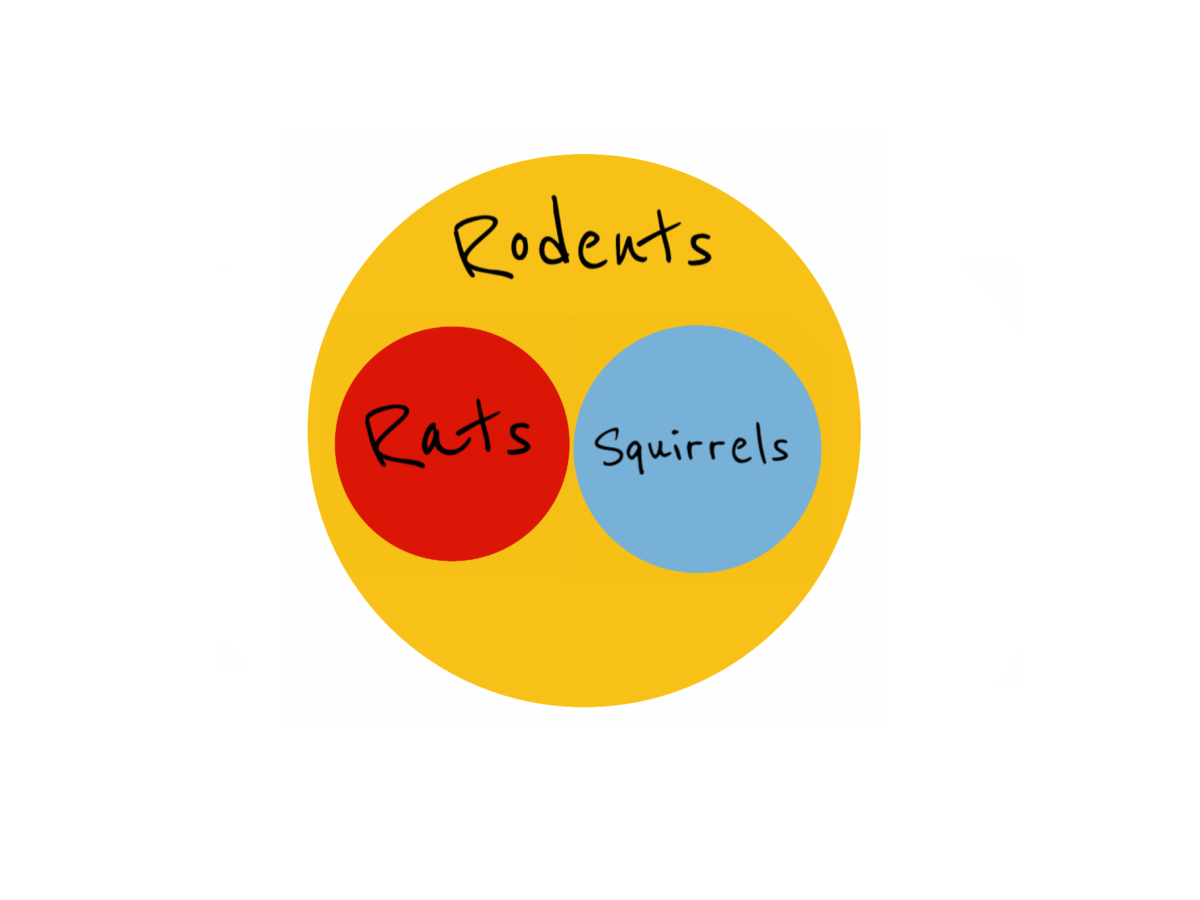
Rats are now not part of this anymore, we move on to the next statement.
All rodents are monkeys
If all rodents are monkeys, this makes the amount of monkeys equal or more than the amount of rodents. The statements do not say that all monkeys are rodents.
Squirrels = or < Rodents = or < Monkeys
This also suggests that all squirrels are also monkeys. Why that is, I don’t know, but that’s the idea.
N o t a l l m o n k e y s a r e s q u i r r e l s
(Irl, no monkeys are squirrels, and no squirrels are monkeys. I think)
Hi @Sarah Alam ! Did you make solutions for the other problems as well?
Log in to reply
One of them, I’m going to do the others soon, I’m just preparing for a big exam. You’ll get them soon.
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Everything is clear and readable |
| Ingenuity | 3/5 | Diagrams, set theory, good |
| Total | 13/15 | Great job! I am really running out of things to say! |
| Accuracy | 4/5 | Some rats could have been squirrels |
| Readability | 5/5 | Its clear and readable |
| Ingenuity | 3/5 | I like the rat added |
| Total | 12/15 | Great job! Percy is running out of things to say just like me |
Let R be the set of all rodents,
S be the set of all squirrels and
T be the set of all monkeys
According to the first statement,
All Squirrels are rodents
=> Squirrels lie in the power set of rodents I.e. squirrels are a part of the set of all rodents i.e,
S ∈ R
Also,since S is a part of R ,the opposite( R ∈ S ) is not true.
Our next statement says,
All rodents are monkeys.
=> Rodents lie in the power set of monkeys I.e. rodents are a part of the set of all monkeys i.e,
R ∈ T
Again,the opposite isn't true
 Venn Diagram
Venn Diagram
Hence,
The biggest set is that of monkeys' in which lies the set of rodents (smaller than that of monkeys' but bigger than squirrels') in which lies the set of squirrels
As you can clearly SEE , ALL MONKEYS ARE NOT SQUIRRELS ……ᘛ⁐̤ᕐᐷ
| Accuracy | 5/5 | Everything is correct |
| Readability | 4/5 | Everything is clear, can't say very readable tho |
| Ingenuity | 1/5 | A touch of set theory |
| Total | 10/15 | Great job! I will update your score on the members and points note! |
Is the Venn diagram clearly visible?just confirming
Log in to reply
I can't see it
| Accuracy | 5/5 | Everything is correct |
| Readability | 4/5 | Its clear, but not very easy to understand |
| Ingenuity | 1/5 | I like the ᘛ⁐̤ᕐᐷ |
| Total | 10/15 | Great job! |
Log in to reply
Can u please tell how do I fix the image issues?
Log in to reply
Please help:'(
If possible can you put down the link of the image here
Log in to reply
@Jason Gomez – Here it is:https://drive.google.com/file/d/1ULPCX2icqSicwnURqWmAPPrTl2h3YG1v/view?usp=drivesdk,thanks
@Jason Gomez – Use this link instead https://ds055uzetaobb.cloudfront.net/uploads/QKplxx7ru6-142ea7cc-c9d2-4890-9ef9-6f451b026ec2.jpeg
I screenshoted it and got through the normal brilliant way of posting pictures
Log in to reply
@Jason Gomez – Thank you ! Though the image wasn't mine,I learnt something.BTW I've put the link so I think it's fine,you need not change ur marks and all:)
Log in to reply
@Agent T – @Percy Jackson Are they doing this on purpose ??
@Tanya Adlakha Please don’t call me sir, I am literally as old as you
Log in to reply
@Jason Gomez – They have to be doing it on purpose. I'm sure its clear we're teens because of our humor.
Log in to reply
@A Former Brilliant Member – my spirit animal is monkey that's why I am respectful :)
Okay @Jason Gomez,I won't call u sir,will call u kiddo from now on ^_^
@Jason Gomez – Well mental age matters ¯_(ツ)_/¯
Log in to reply
@Agent T – Damn it, can’t argue against kiddo now
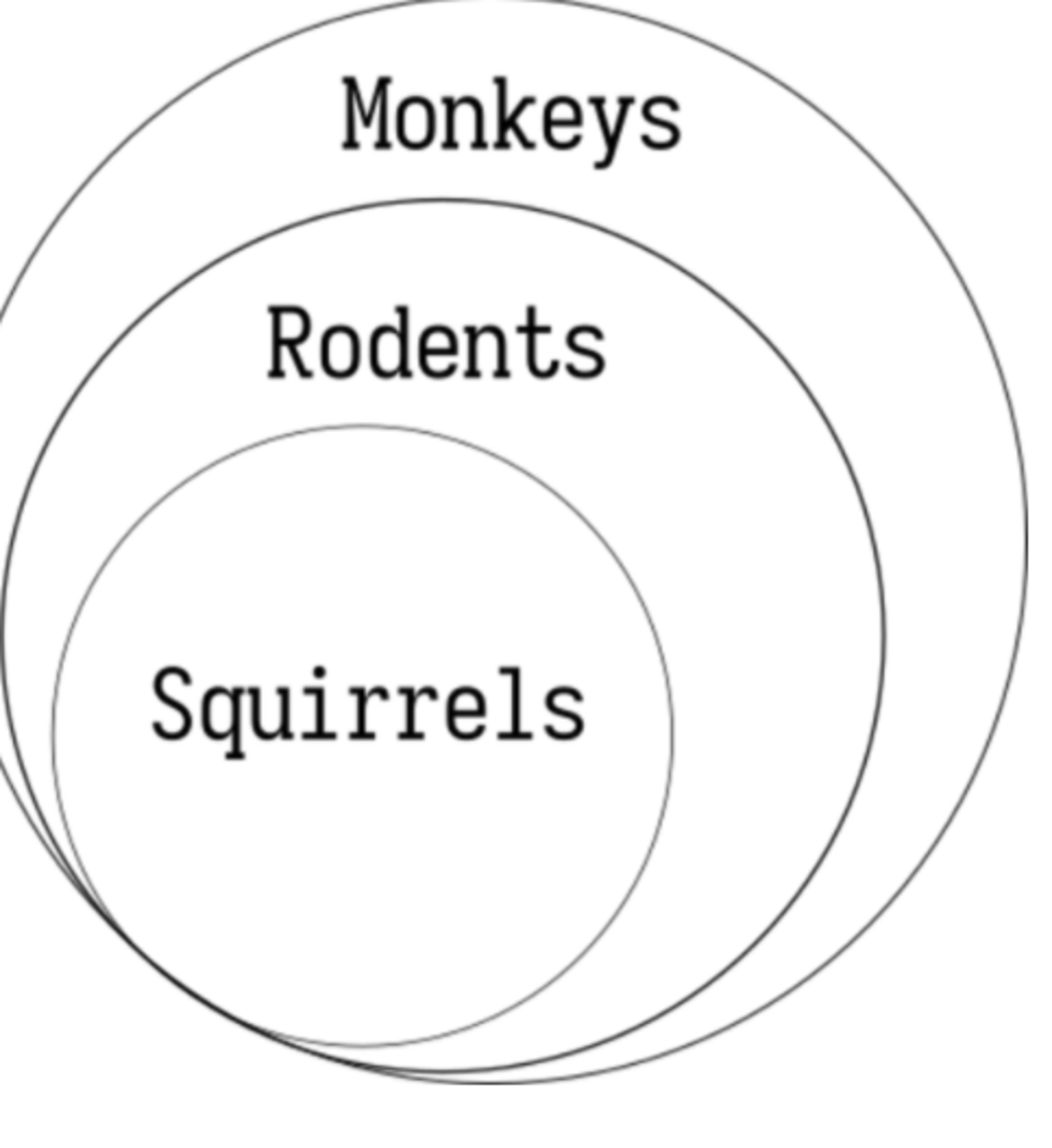 Squirrels are in the set of rodents and rodents are in the set of monkeys but monkeys are an independent set being inside no-one As you can see inside the venn diagram,
Squirrels are in the set of rodents and rodents are in the set of monkeys but monkeys are an independent set being inside no-one As you can see inside the venn diagram,
Uh...I can clearly see that you just posted Oskar's venn diagram... @Jason Gomez What do we do about this?
Log in to reply
Maybe a negative in ingenuity?
| Accuracy | 2/5 | Statements are accurate, but answer isn't given or explained |
| Readability | 1/5 | Oskar's picture doesn't give points |
| Ingenuity | 0/5 | You copied Oskar's picture |
| Total | 3/15 | Great job! I will update your score on the members and points note! |
Log in to reply
I copied his not to steal credit but to show a visual demonstration that I was not able to create myself online Sorry.
Log in to reply
I do not see how you can't whip up a visual demonstration? If you know how to use the internet, you will surely know how to use paint or any drawing tool. I'm sorry but this just shows that your knowledge of the concept isn't very clear, since your explanation is also just one statement.
| Accuracy | 2/5 | Statements are accurate, but answer isn't given or explained |
| Readability | 1/5 | Oskar's picture doesn't give points |
| Ingenuity | 0/5 | You copied Oskar's picture |
| Total | 3/15 | Dont copy from others next time (As judge I am allowed) |
 so in this horrible drawing I express that U set are monkeys and all the compounds in that set are squirrels and rodents, so the logic behind that to say that not all monkeys are squirrels is the following example: Imagine that U set is the universe and in the other sets they are galaxies, then planets, so if I say that all the universes are in planets, it is wrong because all the planets are in the universe (and we know that the universe is not composed only of planets so it is not true) (we can define them as "some"). The explanation is clear that the universe set is not necessarily the set of planets. The same goes for monkeys, monkeys are not necessarily squirrels. (The interesting thing about set theory is that we can never express everything is nothing, just in our mind).
so in this horrible drawing I express that U set are monkeys and all the compounds in that set are squirrels and rodents, so the logic behind that to say that not all monkeys are squirrels is the following example: Imagine that U set is the universe and in the other sets they are galaxies, then planets, so if I say that all the universes are in planets, it is wrong because all the planets are in the universe (and we know that the universe is not composed only of planets so it is not true) (we can define them as "some"). The explanation is clear that the universe set is not necessarily the set of planets. The same goes for monkeys, monkeys are not necessarily squirrels. (The interesting thing about set theory is that we can never express everything is nothing, just in our mind).
@Elijah Frank - Would you like to join the Mathathon? I think you have already asked and you are actively posting solutions, so...if you want to you can join, there's one new spot :)
Log in to reply
Yes of course I want to join, I already have the solutions for the other two problems, I just need to post.
| Accuracy | 5/5 | Everything is correct |
| Readability | 4/5 | Everything is clear but not very good-looking |
| Ingenuity | 2/5 | Venn diagram used |
| Total | 11/15 | Great job! I will update your score on the members and points note! |
@Elijah Frank can I ask u something?
Log in to reply
Sure ask me
| Accuracy | 5/5 | Everything is correct |
| Readability | 4/5 | Not very readable |
| Ingenuity | 2/5 | Nice use of analogy |
| Total | 11/15 | Great job! This is the smallest score table without this text |
Let S denote the set of all squirrels, R denote the set of all rodents and M denote the set of all monkeys, we're given that,
All Squirrels are rodents
All rodents are monkeys i.e,
S ⊆ R ⊆ M
Which means that M is the Universal Set of which R is a subset and S again is a subset of R implying also of M . For the required case to be true, i.e one that says "All monkeys are squirrels" we need M ⊂ S , but since already S ⊂ M , for the required condition to be true S = M .
From the given two statements two conditions arise,
- R is a proper subset of M , R < M , not all elements of M are in R
Since S is a subset of R , S will always be less than M too.
- R is an improper subset of M , R = M , every element of M is in R
Since S is a subset of R , either it is a proper subset S < ( R = M ) or an improper one S = ( R = M ) .
In the above conditions, only one, S = ( R = M ) or S = M supports the required case, since it is not necessarily true that S = M , it is not necessarily true that "All monkeys are squirrels" .
For the sake of generality we've not considered trivial improper subsets, or null subsets, though if R is null, S is also null which doesn't support the required case either.
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Proper latex has been used and well structured answer |
| Ingenuity | 4/5 | Set theory and set notation has been used well |
| Total | 14/15 | Great job! I will update your score on the members and points note! |
Log in to reply
I was planning of using the venn diagram, got lazy and thought it'd be cliché, no worries, thanks though.
| Accuracy | 4/5 | Monkeys ain’t the Universal Set, we demigods exist too |
| Readability | 5/5 | Well structured answer |
| Ingenuity | 3/5 | Set theory has been well used |
| Total | 12/15 | Great job! Percy will update your score on the members and points note ?? |
Log in to reply
Actually, monkeys is a universal set, they're subjective sets
Most Common Solution -
All squirrels are rodents. This means that every last squirrel on this planet is a rodent. This doesn't necessarily mean that all rodents are squirrels, here's how -
We can say that all apples are fruits. This doesn't mean all fruits are apples. Mangoes and bananas aren't apples. So, if all A are B, that doesn't mean all B are A.
So, not all rodents are squirrels.
Now, the second statement states, 'All rodents are monkeys' and again same thing, all rodents are monkeys, but not all monkeys are rodents.
Not all monkeys are rodents, which means that there are some monkeys that are not rodents. These monkeys aren't squirrels either, because all squirrels are rodents. Thus, the answer is No
how to put text in a box.
It appears like B o t h a r e . . .
and how to make text larger. I know that \large and others are used but I don't understand the syntax
Please notify me for this problem as well if any more solutions come (I don’t want to keep checking after I finish, may do if I somehow am able to correct all solutions)
Maybe being judge means you have to solve the problem first all the time?
Uh...maybe? Wdymn by that?
Log in to reply
I was the first one to solve both the first and second problem
Log in to reply
lmao no one other than you has solved this one yet
Log in to reply
@A Former Brilliant Member – But it shows two solvers so someone else has also solved it (after I did)
Log in to reply
@Jason Gomez – No, it shows 1 solver by default. Its because I technically 'solved it'. I can see the views and solvers, so I know only the both of us have done it :P
Log in to reply
@A Former Brilliant Member – Heh but when I had solved it did show only one solver, maybe a bug, but usually it shows no number if no one solved it so.…