All that matters is the constant velocity!
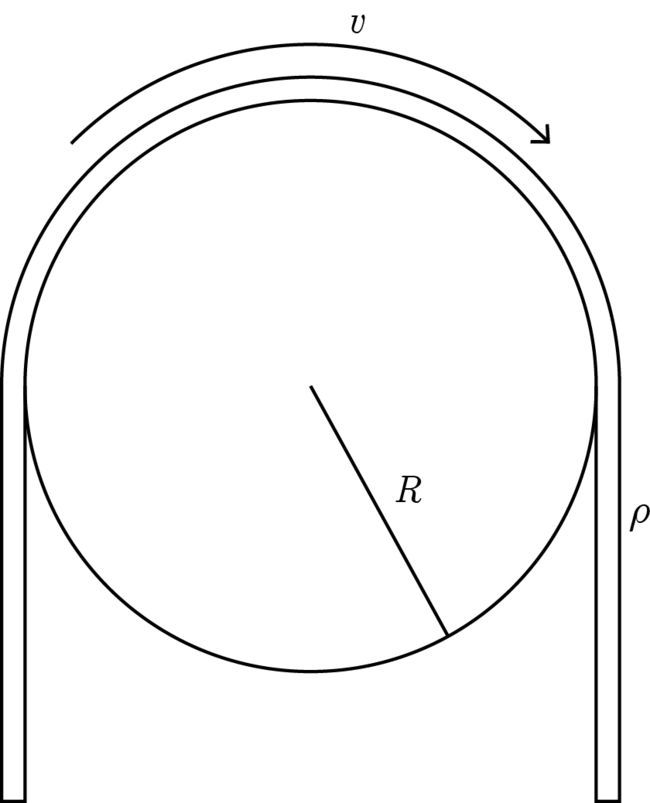 There is a thin string of linear mass density
ρ
, which is going around a pulley of radius
R
, with constant velocity
v
.
There is a thin string of linear mass density
ρ
, which is going around a pulley of radius
R
, with constant velocity
v
.
Determine the internal tension in the string.
Details and Assumptions
-
There is no net force acting on the pulley-string system.
-
Neglect gravity.
-
Take ρ = 0 . 2 5 kgm − 1 , R = 0 . 2 5 m , v = 1 3 ms − 1 .
The answer is 3.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Tension is constant because there is no friction.
And I think it is highly overrated.
I too did the same. But I did a mistake somewhere.
Is the tension in the constant everywhere
Log in to reply
Yes, because the thread moved with constant velocity
Hey @Kishore S Shenoy , why did u take tension constant everywhere?? How the tension be same in both directions??
Log in to reply
Tension is same because the thread is going with constant velocity.
Log in to reply
Why should it be constant even though it moves with constant velocity?
Log in to reply
@Surya Prakash – Since all go at same velocity, net force on all the small masses should be 0. Thus using Newton's 3rd Law, Tension is same throughout
Log in to reply
@Kishore S. Shenoy – How can net force on a small piece of string be zero if it is moving in a circle ? It will have radial acceleration.
Hi Kishore, could you please explain how you got your first eqquation N = 2 T sin ( 2 d α ) ?
Log in to reply
Taking Component of the Tension along the normal direction of the pulley. Which part of the equation do not understand?
even gravitational force acts nthen why you did not consider that
Log in to reply
You have to ignore gravity. Check the "Details and Assumptions" part.
normal exerted by the pulley will be outwards not inwards
normal force exerted by the pulley on the small element in the string will be out wards not inwards
Log in to reply
The point to be understood here is that the pulley does not provide any force on the string. I've mentioned it that way so that it's easy to understand. The pulley's presence is for mere aid for thought, whatsoever.
2Tsin(dp\2) - N=dm ac ac centripetal acceleration
Cant we do it like this that...
T = d ( t ) d ( m v )
T = d t d m × v
Now we know d m = ρ . d x . So d t d m = ρ × d t d x = ρ v .
So putting in the 1st eqn we get
T = ρ v 2
T = 3 . 2 5 N .
Is My solution logically ok?
@Md Junaid Its not correct....the final result came same due to dimensions
I guess. Since you've solved from the Third Law. Note that I've not checked it completely. If you have assumed something, please put up.
your solution is correct his solution is wrong according to me
Take a small mass d m making an angle d α at the centre.
So, to find Normal N on the pulley,
N = 2 T sin 2 d α ≈ T d α
Now for it to rotate with constant velocity v , N = d m a c = R d m v 2
⇒ T d α = ρ R d α R v 2 = ρ v 2 d α ⇒ T = ρ v 2
∴ T = ρ v 2 = 3 . 2 5
Note : The tension is independent of the radius of the pulley.