Almost 0

I was just about to get to sleep when this idea struck through my head.

I'll give you an example with... erm, let's say, $7\times7$ grid.

---

I'm going to make a "staircase" from two opposing vertices of the grid, like above.

Let each region $\text{PINK}$ and $\text{GREEN}.$

It's clear that both the shaded region have the sum of $0.$

$\text{PINK}+\text{GREEN}=0.$

But then as the image above shows, if we add $\text{PINK}$ and $\text{GREEN},$ we are adding the $\text{ORANGE}$ region twice, and never adding the $\text{WHITE}$ region.

Then we can say that

$\begin{aligned} S &=\text{PINK}+\text{GREEN}-\text{ORANGE}+\text{WHITE} \\ &=\text{WHITE}-\text{ORANGE} \end{aligned}$

Also know that there are always one more room for $\text{WHITE}$ than for $\text{ORANGE},$

and that $\text{WHITE}$ and $\text{ORANGE}$ are, of course, independent.

---

Get back to the original $2017\times2017$ grid.

And there are $1009$ rooms for $\text{WHITE}$ , and $1008$ rooms for $\text{ORANGE}$ since there are a total of $2017$ rooms for $\text{WHITE}$ and $\text{ORANGE}.$

Since the maximum of $\text{WHITE}$ is $1009$ and the minimum of $\text{ORANGE}$ is $-1008,$

it's obvious that the maximum of $S$ is $1009-(-1008)=\boxed{2017},$

when all the rooms of $\text{WHITE}$ are filled with $1$ and all the rooms of $\text{ORANGE}$ are filled with $-1.$

Which is possible, when we fill the grid like:

---

Note that we can also prove that $S$ has a minimum of $-2017,$ when all the rooms of $\text{WHITE}$ are filled with $-1$ and all the rooms of $\text{ORANGE}$ are filled with $1.$

Please comment below if I got any... grammar problems or any calculation mistakes. I'm really sleepy, so yeah.

Number the entries in the grid $a(0,0)$ through $a(N,N)$ . (Here, $N = 2016$ .)

It is easy to prove by induction that $a(x,y) = (-1)^y a(x,0) + (-1)^x a(0,y) - (-1)^{x+y} a(0,0).$ This may also be written as $a(x,y) = (-1)^{x+y}(b(x) + c(y) - d),$ with $b(0) = c(0) = d$ and $|b(x)|, |c(y)|, |d| \leq 1$ . These are the $2N+1$ degrees of freedom of the system. The constraint is $|b(x) + c(y) - d| \leq 1.$ Let $N = 2n + 1$ . Then the sum is $S = \sum_{x = 0}^N \sum_{y = 0}^N (-1)^{x+y} (b(x) + c(y) - d) \\ = \sum_{x = 0}^N (-1)^x b(x) + \sum_{y = 0}^N (-1)^y c(y) - d \\ = \sum_{x = 1}^N (-1)^x b(x) + \sum_{y = 1}^N (-1)^y c(y) + d.$ To maximize this, we wish to maximize $b(x)$ for even $x$ and minimize it for odd $x$ ; and similar for $y$ . Without loss of generality we can make a regular pattern with $b(2i) = p, b(2i+1) = -q, c(2j) = r, c(2j+1) = -s,\ \ \ \ \ 1 \leq i,j \leq n.$ Of course, $|p|,|q|,|r|,|s| \leq 1$ . The goal is to maximize $S = n(p + q + r + s) + d$ . The constraints become $|p + r - d|, |r - q - d|, |s - p + d|, |q + s + d| \leq 1.$ Now $p + q + r + s = (p+r-d)+(q+s+d) \leq |p+r-d| + |q+s+d| \leq 2,$ so that $S \leq 2n + d \leq N$ .

I claim that equality is actually possible, so that the solution is $\boxed{S = N = 2017}$ .

To see this, check for each $\leq$ sign when equality attains. In order for $2n + d = N = 2n+1$ , we must have $d = 1$ . Since $p+r-d, q+s+d \leq 1$ , their sum is only $= 2$ if each equals one. This, in turn, requires $p = r = 1$ and $q = -s$ . When these conditions are fulfilled, we actually attain the maximum value.

What does this pattern look like?

$\begin{array}{cccccc} 1 & s & 1 & s & \cdots & 1 \\ -s & -1 & -s & -1 & & -s \\ 1 & s & 1 & s & \cdots & 1 \\ -s & -1 & -s & -1 & & -s \\ \vdots & & \vdots & & \ddots & \vdots \\ 1 & s & 1 & s & \cdots & 1 \end{array}$

The choice $s = \pm 1$ , gives alternating constant rows or constant columns, as others have posted. With $s = 0$ we get a solution in which half of the numbers in the grid is zero.

First, let's show that we can obtain $2017$ for the sum...

Fill the first row with one's and fill every other row after that alternatively with -1's and 1's. For example for a 5x5 this would look like this:

If we extended this to $2017 \times 2017$ , clearly the sum would be equal to $2017$ .

---

Now, to show that $2017$ is the highest sum you can attain...

Let's label the entry of row $m$ column $n$ as $N_{m,n}$ .
We have the following observations:

1. The sum of all the boxes with $m$ and $n$ less than $2017$ is $0$ . (Since all the little 2x2 sub boxes that it is made up of sum to $0$ )
2. The maximum that $N_{2017,2017}$ can be, of course, is $1$ .
3. For odd integers $n$ and $m$ , we can verify that $N_{2017,n} + N_{2017,n+1} + N_{m,2017} + N_{m+1,2017} = N_{m,n} - N_{m+1,n+1}$ . (Can you prove this?) Hence, this expression is at most $1 - (-1) = 2$ .

Thus, if we split the sum up into 1) the top left $2016 \times 2016$ grid, 2) the bottom right most square, and 3) the 2017th row and 2017th column, then it can be expressed as

$\text{Sum } = \left(\sum_{i=1}^{1008} \sum_{j=1}^{1008} N_{2i-1,2j-1} + N_{2i, 2j-1} + N_{2i, 2j-1} + N_{2i, 2j} \right) + \left( N_{2017,2017} \right) + \left( \sum_{i=1}^{1008} (N_{2017,2i-1}+N_{2017,2i} + N_{2i-1,2017} + N_{2i, 2017} ) \right)$

$\leq 0 + 1 + 2 \times 1008$

$= \boxed{2017}$

Here's the idea that opened me up the way to the solution:

Every $n\times n$ grid with even $n$ has sum $0$ . That's quite obvious but very important conclusion. A $n\times n$ with odd $n$ looks like this (I randomly chose $7\times 7$ grid):

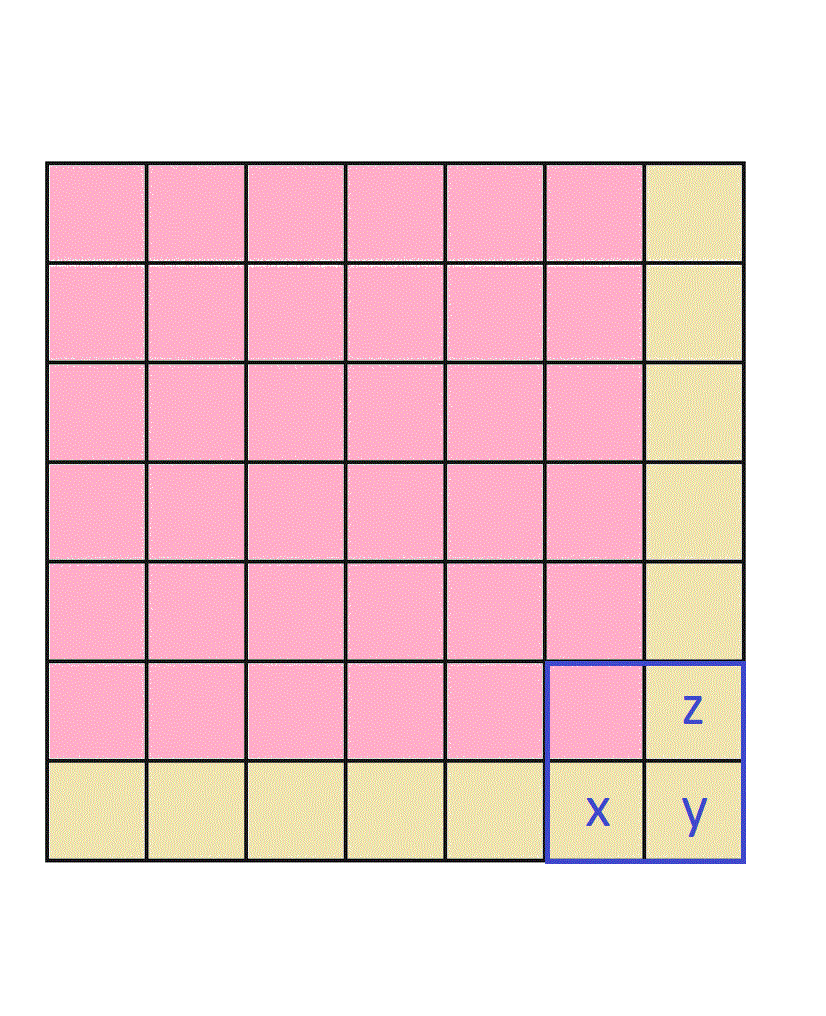
and it sum comes down to the sum of yellow squares because pink part is actually an even-n grid which, we know, sums to $0$ .

When I saw that, I said to myself: Hey, can I put 1 in each yellow square?

I immediately realized that it will be imposible since it won't satisfy the rule that the sum of every $2\times 2$ grid has to be $0$ . But, that led me to another obvious but precious thing:

Since the sum of the blue-wired $2\times 2$ grid in the left-bottom corner must be $0$ , then maximum sum of the three yellow squares inside it, marked $x$ , $y$ and $z$ , must be $1$ . Also, it seems logical that, in order to maximize the sum of the yellow part, we should fill it with greatest possible values that would fit.

Now, trying out by plugging in some values, we see that when we set $(x,y,z)=(0,1,0)$ and complete the rest of the grid by following the rules, we get maximum sum for the yellow part as well as for the whole grid. Yellow part of the $7\times 7$ grid, then, consists of $2017$ 1s and $2016$ 0s. Hence, maximum sum is $\boxed{2017}$ .

P.S. There are other possible ways to fill the grid, like @Arjen Vreugdenhil , @Geoff Pilling and @H.M. 유 showed.

The claim is that for any $(2n + 1) \times (2n + 1)$ grid with $n \geq 1$ satisfying the conditions above, the maximum value of $S$ is $2n + 1$ . Moreover, a grid that maximizes the sum is of the form

. We proceed by induction on $n \geq 1$ . For the base case, consider a $3 \times 3$ grid of the form

. Using the assumptions, we can write $0 = (x_1 + x_2 + x_3 + x_4 + x_5 +x_6 + x_7 + x_8 + x_9) + ( x_2 + x_4 + x_6 + x_8) + 3x_5$ , or $S = -(x_2 + x_4 + x_6 + x_8 + 3x_5)$ . Note that $x_2 + x_3 + x_5 + x_6 = 0$ , or $x_2 + x_5 + x_6 = -x_3$ . Similarly, $x_4 + x_5 + x_7 + x_8 = 0$ means $x_4 + x_5 + x_8 = -x_7$ . Then it follows that $S = -(x_2 + x_4 + x_6 + x_8 + 2x_5) - x_5 = x_3 + x_7 - x_5$ . Since we want to maximize, choose $x_3 = 1$ , $x_7 = 1$ , $x_5 = -1$ . These choices force us to create the grid

and we get $S = 3$ .

For the induction hypothesis, suppose that for a $(2n + 1) \times (2n + 1)$ grid with $n \geq 1$ satisfying the conditions above, the maximum value of $S$ is $2n + 1$ , and that the grid is of the desired form. We want to show that this is true for the $2(n+1) + 1 \times 2(n+1) + 1$ grid as well. Consider the grid

. The $2n+1 \times 2n+1$ grid is maximized by the induction hypothesis; it is not hard to see that $\sum_{i = 1}^{2n+2} x_{i, 2n+2} + x_{i, 2n+3} + x_{2n+2, i} + x_{2n+3, i} = 0$ , which implies that $\sum_{i = 1}^{2n+2} x_{i, 2n+2} + x_{i, 2n+3} + x_{2n+2, i} + x_{2n+3, i} - x_{2n+2, 2n+2} = -x_{2n+2, 2n+2}$ . Let $S^* = \sum_{i = 1}^{2n+2} x_{i, 2n+2} + x_{i, 2n+3} + x_{2n+2, i} + x_{2n+3, i} - x_{2n+2, 2n+2}$ ; we note that we are trying to maximize $S^* + x_{2n+3, 2n+3} = -x_{2n+2, 2n+2} + x_{2n+3, 2n+3}$ , so we choose $x_{2n+2, 2n+2} = -1$ and $x_{2n+3, 2n+3} = 1$ . Now, it follows easily that the grid is of the form

and $S = 2(n+1) + 1$ .

Sum of all cells of the grid = sum of diagonals cells, hence for 2017 grid it is 2017

Obiously, any 2n*2n grid has a resulting S of "0". So maximum S value for a 2n+1 grid is achieved by adding 2n+1 "1's". Alternating columns of "1's" and "-1's" results in a maximun value for S of 2017.