1700 Followers problem!

Algebra Level 5

Consider two complex numbers: $z_1$ : $692+3745\sqrt{3}i$ and $z_2$ : $692+1729\sqrt{3}i$ .

There exists another complex number $z$ such that $\text{arg}\left(\dfrac{z-z_1}{z-z_2}\right)=\dfrac{\pi}{3}$ .

Then , Find the value of $|z+316-2737\sqrt{3}i|$

Details And Assumptions:

$\text{arg}(z)$ is the argument which means the angle made by the complex number $z$ with the positive X axis.
$|z|$ represents the modulus of complex number $z$ .
$i=\sqrt{-1}$

Inspiration .

This problem is original.

The answer is 2016.

3 solutions

Nihar Mahajan
Nov 10, 2015

If we have graphical representation of the numbers in complex plane , we find that $z,z_1,z_2$ lie on a circle with center $O$ . Without loss of generality we let $OM \ || \ X \ axis$ where $M$ is mid point of $Z_1Z_2$ so that it becomes easier to compute distances. Thus we have:

$M=\left(692,\dfrac{3745\sqrt{3}+1729\sqrt{3}}{2}\right)=\left(692,\dfrac{5474\sqrt{3}}{2}\right)=(692,2737\sqrt{3})$

$MZ_1=3745\sqrt{3}-2737\sqrt{3}=1008\sqrt{3}$

We note that $\Delta OMZ_1$ is a $30-60-90$ triangle , and we have $OM=1008$ .Hence we have:

$O=(692-1008,2723\sqrt{3})=(-316,2723\sqrt{3})$

So the question asks for distance $OZ$ which is actually the circumradius and since $\Delta OMZ_1$ is a $30-60-90$ triangle , we have circumradius $=1008\times 2=\boxed{2016}$

Moderator note:

When dealing with complex number norms and arguments, it is often helpful to consider the graphical representation directly:

Why is the locus of points that satisfy $\text{arg}\left(\dfrac{z-z_1}{z-z_2}\right)=\dfrac{\pi}{3}$ given by a circle?

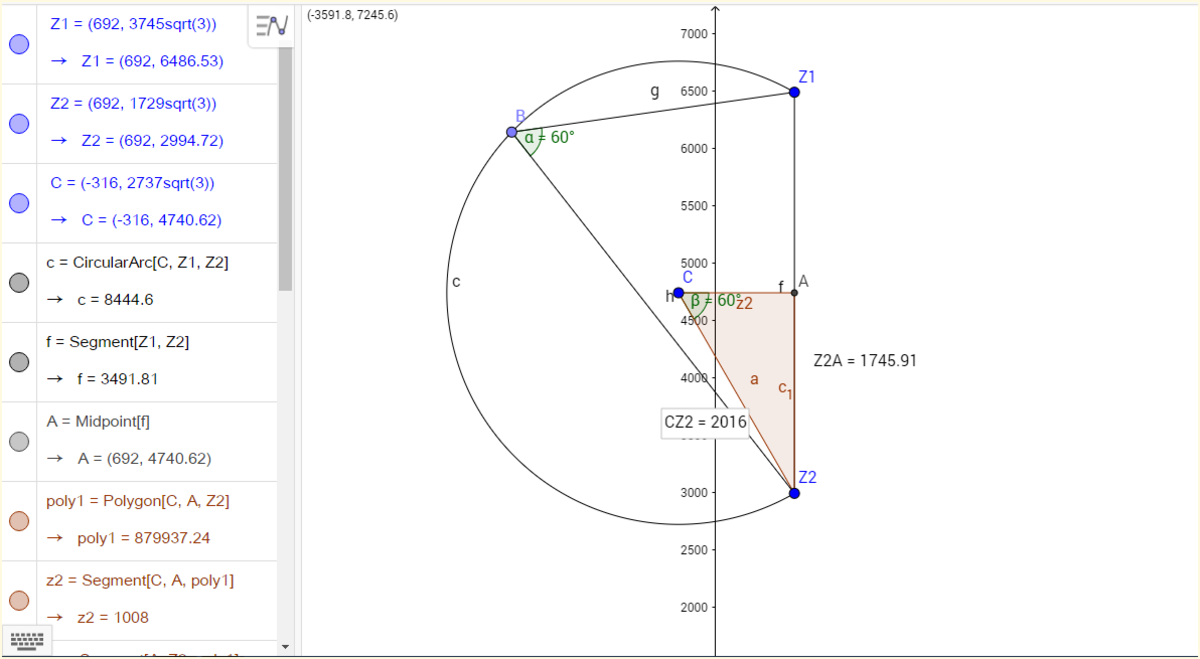
You should revise the problem, because I think there is more than one answer. Here's my approach: the angle condition can be expressed as: $\arg \left( {\frac{{z - z_1 }}{{z - z_2 }}} \right) = \frac{\pi }{3} = \arg \left( {z - z_1 } \right) - \arg \left( {z - z_2 } \right)$ That equation can be interpreted as follows: the line containing $z$ and $z_1$ leads the line containing $z$ and $z_2$ by $60^\circ$ . Graphically is like this:

Image

Applying simple geometry it can be found that: $z = - 1324 + 1729\sqrt 3 i$ The angle condition is satisfied: $\arg \left( {\frac{{z - z_1 }}{{z - z_2 }}} \right) = \arg \left( {\frac{{ - 1324 + 1729\sqrt 3 i - 692 - 3745\sqrt 3 i}}{{ - 1324 + 1729\sqrt 3 i - 692 - 1729\sqrt 3 i}}} \right) = \arg \left( {\frac{{ - 2016 - 2016\sqrt 3 i}}{{ - 2016}}} \right) = \arg \left( {1 + \sqrt 3 i} \right) = \frac{\pi }{3}$ However: $\left| {z - 1700 - 2737\sqrt 3 i} \right| = \left| { - 1324 + 1729\sqrt 3 i - 1700 - 2737\sqrt 3 i} \right| = \left| { - 3024 - 1008\sqrt 3 i} \right| = \sqrt {3024^2 + 3 \cdot 1008^2 } = 2016\sqrt 3 \ne 2016$ The only reason I could solve this problem was because I solved your inspiration problem and read the comments. You should check if that angle condition really defines a circle, because as you can see, the solution I found satisfies the condition but yields a different answer.

Daniel Turizo - 5 years, 7 months ago

Thanks I see that my solution is incomplete and I have missed out few cases. I am currently out of station , so I will try to complete it later. For the time being I have appropriately edited the question. I apologise for the inconvenience caused.

Nihar Mahajan - 5 years, 7 months ago

Nice way to get the answer to 2016. U can treat it as a coordinate geometry problem.

Aditya Kumar - 5 years, 7 months ago

Can you update the solution (or remove the last paragraph) so that I can start to review it?

Calvin Lin Staff - 5 years, 6 months ago

@Calvin Lin – Updated it.

Nihar Mahajan - 5 years, 6 months ago

@Nihar Mahajan

Your description also describes a circle, since no matter what the angle line $zz_{2}$ makes with the x-axis, $\angle z_{2}zz_{1}$ would always be 60 degrees. This means that the answer would have far more solutions than $2016\sqrt{3}$ and $2016$ . I remembered that when I solved the problem, I also got a circle with radius 2016 and thus directly imput my answer as 2016. Now, backtracking my solution, my circle also has center $-316, 2737\sqrt{3}$ , and this is the same as the circle that is described in your solution. this means the question has to be changed to finding the answer to $|z+316-2737\sqrt{3}i|$ for the answer to be $2016$ for all possible $z$

I'm still analysing Nihar's solution

UPDATE: The error in Nihar's solution is that the x-coordinate for $O$ should be $692-1008$ instead of $692+1008$

Julian Poon - 5 years, 7 months ago

See my solution, I hope to have explained everything.

Ajinkya Shivashankar - 4 years, 5 months ago

Ajinkya Shivashankar
Jan 3, 2017

Solution 1:- The given equation is a circle as the angle subtended by a chord in a circle is constant.(And half the angle subtended at the centre).

So we would like to calculate the radius of the given circle. And guess what?

... We are given 2 points which lie on the circle and its centre is also known (Centre is $-316+2737\sqrt{3}i$ ).

So the distance between 2 points in the complex plane is $\sqrt{(692+316)^2+3*(3745-2737)^2}=\sqrt{(1008)^2+3*(1008)^2}=2*1008=2016$

But what if we do not know the centre?

Solution 2:- Still we could find the radius by dropping a perpendicular from the centre onto the chord formed by the 2 points. We can easily calculate the distance between the 2 points and perpendicular from centre bisects the chord. So we have 1 side of the right angle triangle. All we need is 1 angle.

This can be found by using the fact that the angle subtended by the chord on the circle (which we know is $\frac{\pi}{3}}$ ) is half the angle subtended by the chord at the centre. And the perpendicular from centre bisects the angle as well. So the answer follows using $sin(\theta)$

But what is this?

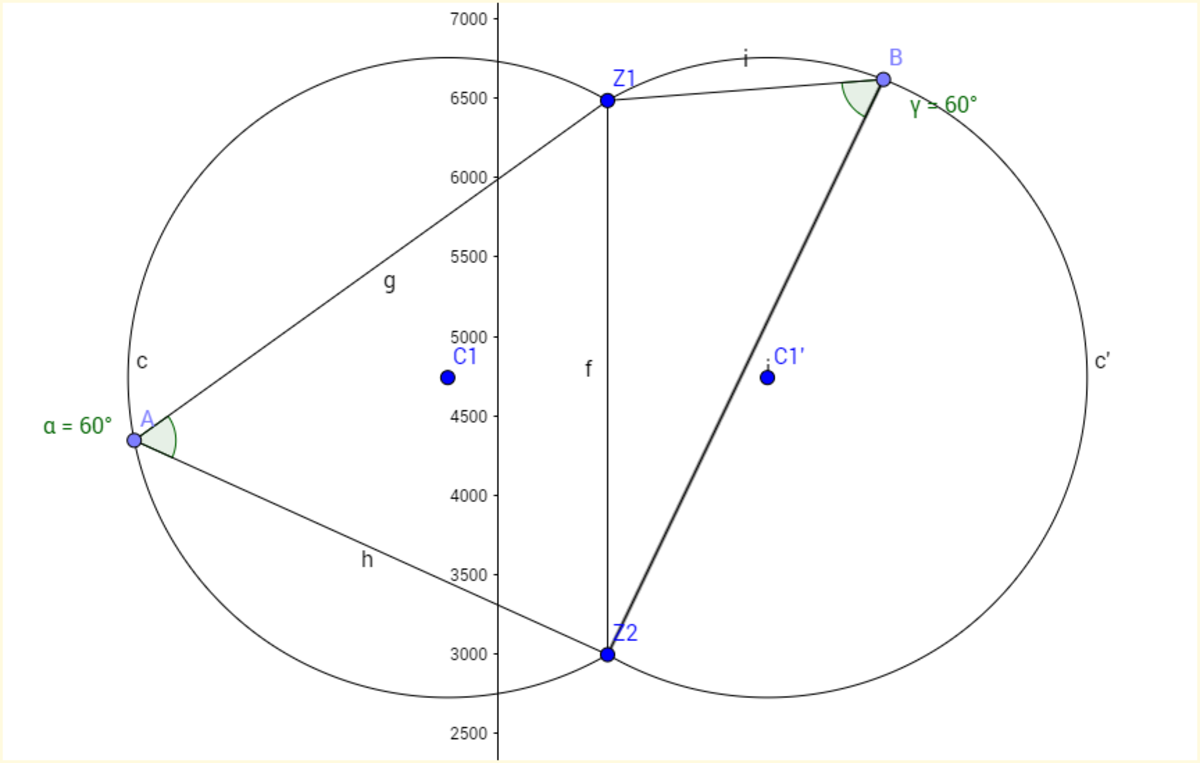
This is the actual graph you get when you solve the equations. However since the distance was asked only from C1 I have omitted this in the 1st diagram. Every point on both arcs satisfies the equation given above and so this might give extra answers.

Lu Chee Ket
Nov 11, 2015

First thing came to my mind was an equilateral triangle inside a circle; it follows that $z_1$ to $z$ and then to $z_2$ makes a $60^\circ$ always of other triangles on one side and $120^\circ$ on another side. (1700, 2737 $\sqrt3$ ) must be the center of the circle as path of z in order to get a constant modulus for a distance of z from it. The diagram shown here by Nihar Mahajan should take its mirror image because 1700 > 692. arg z is having same status as ln z for imaginary and real respectively in an index of e; division is just subtraction in the realm as angle formed from division of two complex numbers can just be considered separately for subtraction.

Therefore, just take | $z_1$ - 1700 - i 2737 $\sqrt3$ | or | $z_2$ - 1700 - i 2737 $\sqrt3$ | = 2016 for an answer.

Take simplest z of (3716 + i 2737 $\sqrt3$ ) to check, simply 692 + 3 $\times$ (1700 - 692) - 1700 = 2016.

1700 Followers problem!

This problem is original.

The answer is 2016.

3 solutions

Moderator note:

0 pending reports