Almost 60 followers problem
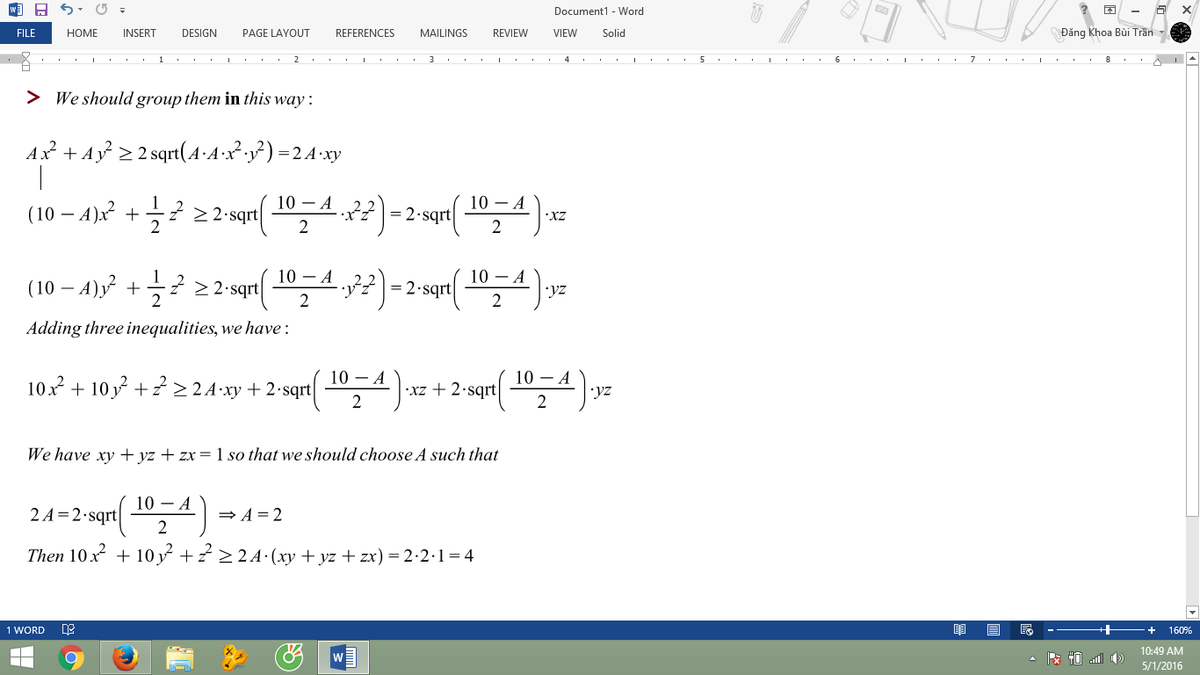
1 0 x 2 + 1 0 y 2 + z 2 Let x , y , z be positive real numbers that satisfy x y + y z + x z = 1 .
Find the minimum value of the expression above.
Give your answer to 2 decimal places
The answer is 4.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Nice solution from the Master again. Must really relearn eigenvalues. Upvote!
How did you group them so nicely in the first place? Some eigenvalues + kernel thing?
Log in to reply
Yes, exactly; you can read my thoughts now (a little scary...). I used eigenvectors to find that z = 4 x = 4 y ... then we know how to group them ;) Writing it up is much quicker if we just form squares.
Log in to reply
Be right back. Doing some fancy linear algebra.
Log in to reply
@Pi Han Goh – I'm doing some (not so fancy) house cleaning... I will not be online much today.
Log in to reply
@Otto Bretscher – Okay I got the eigenvalues for the quadratic form for (10x^2+10y^2 + z^2) to be 1, 10, 10. What's next?
@Otto Bretscher Can you explain the methos / give some reference please? Thank you!
AM-GM? I used Cauchy-schwarz TT.TT
( 1 2 + 1 2 + 2 2 ) ( ( 2 x ) 2 + ( 2 y ) 2 + z 2 ) ≥ ( 2 x + 2 y + 2 z ) 2
( 6 ) ( 4 x 2 + 4 y 2 + z 2 ) ≥ 4 ( x + y + z ) 2
4 x 2 + 4 y 2 + z 2 ≥ 3 2 ( x 2 + y 2 + z 2 + 2 ( x y + y z + x z ) )
4 x 2 + 4 y 2 + z 2 ≥ 3 2 ( x 2 + y 2 + z 2 + 2 ) (Since x y + y z + x z = 1 )
3 1 0 x 2 + 1 0 y 2 + z 2 ≥ 3 4 (Transposition)
1 0 x 2 + 1 0 y 2 + z 2 ≥ 4
great solution, an upvote for you my friend, but it supposed to be 1 2 + 1 2 + 2 2 on the LHS
Log in to reply
Whoah, sorry, didn't notice that... Thanks anyway :)
I first tried symmetry in x , y , and z , but it didn't work -- presumably because the two equations are not mutually symmetric in z (substituting just y = x gives the expression as 2 0 x 2 + z 2 and the equation as x 2 + 2 x z = 1 ). But if you want to go this way, you could take just the symmetry in x and y and proceed from there:
Solve the previous equation for z to get z = 2 x 1 − x 2 and z 2 = 4 x 2 1 − 2 x 2 + x 4 = 4 1 x − 2 − 2 1 + 4 1 x 2 .
Substitute into the expression to get 2 0 x 2 + 4 1 x − 2 − 2 1 + 4 1 x 2 = 4 1 x − 2 − 2 1 + 4 8 1 x 2 .
Now, by AM-GM, 4 1 x − 2 − 2 1 + 4 8 1 x 2 ≥ − 2 1 + 2 4 1 x − 2 ∗ 4 8 1 x 2 = − 2 1 + 2 ( 4 9 ) = 4 .
Equality occurs when 4 8 1 x 2 = 4 1 x − 2 , i.e. x 4 = 8 1 1 , i.e. x = 3 1 , y = 3 1 , z = 3 4 .
Let x = κ , y = κ , z = 1 0 κ .
The above ratio is taken so as to have symmetry to get minimum.
Thus κ = 1 / ( 1 + 2 1 0 ) .
Now putting in given expression min value is
≈ 4 . 0 9 5 .
No, it's exactly 4 ;)
Happy Victory Day, Comrade!
( 2 x − 2 y ) 2 + ( 4 y − z ) 2 + ( 4 x − z ) 2 = 2 0 x 2 + 2 0 y 2 + 2 z 2 − 8 x y − 8 y z − 8 x z ≥ 0 so that 1 0 x 2 + 1 0 y 2 + z 2 ≥ 4 x y + 4 y z + 4 x z = 4 . The minimum is 4 , attained when x = y = 3 1 and z = 3 4