Alternating Current Series #1
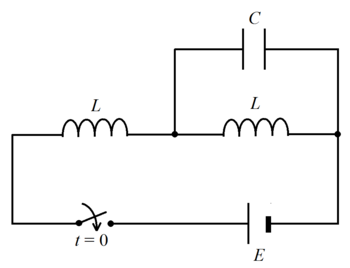
An ideal inductor of inductance L is connected in series with another inductor of inductance L parallel to an ideal capacitor of capacitance C , a battery of electromotive force E , and a switch. Before closing, the switch has been open for a long time and the capacitor is uncharged. The voltage on the capacitor at time t after the switch is closed is given by:
V = α E ( 1 − cos ( L C β t ) )
Find α + β .
The problem is taken from my Physics book.
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Steven Chase
Nice solution
Upvotes have been awarded
@Steven Chase
Right now I am staring at your anayltical solution.
Last night I was feeling very sleepy, therefore I didn't able to take a look.
I didn't understand the step below (Homogeneous equation. )
Log in to reply
Suppose you have a differential equation of the following form:
y ¨ = − ω 2 y + c
The first step is to solve the "homogeneous equation", which is the same equation without the constant.
y ¨ = − ω 2 y
Let the solution to that be y h . Then the full solution is y h + d , which accounts for there being a constant in the original differential equation.
Log in to reply
@Steven Chase
Yeah Thanks for explaining.
One more thing to want to ask.
How did you know that
\ddot{V_{c}(0) =\frac{E}{LC}
?
Can you explain it's physical significance?
Log in to reply
@Talulah Riley – That comes from:
E − 2 V C = L C V ¨ C V C ( 0 ) = 0
The first equation is derived in the body of the solution.
Log in to reply
@Steven Chase
–
@Steven Chase
ohkay
My new problem is up now
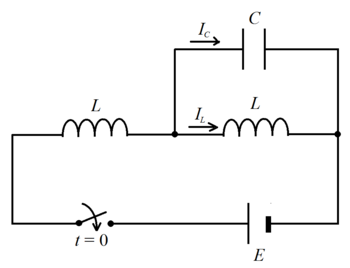
Let the currents through the inductor and the capacitor of the parallel circuit be I L and I C respectively. Then the voltage on the capacitor:
V ( t ) d t d V ( t ) ⟹ I C ( t ) = V ( 0 ) + ∫ 0 t C I C ( τ ) d τ = ∫ 0 t C I C ( τ ) d τ = C I C ( t ) = C d t d V ( t ) Since the capacitor is uncharged at t = 0 ⟹ V ( 0 ) = 0
Note that the voltage on the capacitor is the same as the voltage of the parallel inductor. Then V ( t ) = L d t d I L ( t ) . We also note that:
L d t d ( I L ( t ) + I C ( t ) ) + V ( t ) L d t d I L ( t ) + L C d t 2 d 2 V ( t ) + V ( t ) L C d t 2 d 2 V ( t ) + 2 V ( t ) = E = E = E Note that V ( t ) = L d t d I L ( t )
Solving the differential equation (see Note):
⟹ V ( t ) I C ( t ) I C ( 0 ) ⟹ V ( t ) V ( 0 ) ⟹ V ( t ) = c 1 sin ( C L 2 t ) + c 2 cos ( C L 2 t ) + 2 E = C d t d V ( t ) = L 2 C ( c 1 cos ( C L 2 t ) − sin ( C L 2 t ) ) = c 1 L 2 C = 0 = c 2 cos ( C L 2 t ) + 2 E = c 2 + 2 E = 0 = 2 E ( 1 − cos ( C L 2 t ) ) where c 1 and c 2 are constants. ⟹ c 1 = 0 ⟹ c 2 = − 2 E
Therefore α + β = 2 + 2 = 4 .
Note : Consider a differential equation d t 2 d 2 v ( t ) + p v ( t ) = q . Then the characteristic equation ( D 2 + q ) v = 0 , ⟹ D = ± i p and the general solution of the differential equation is:
v ( t ) d t d v ( t ) d t 2 d 2 v ( t ) ⟹ d t 2 d 2 v ( t ) + p v ( t ) − p v ( t ) + p c 3 + p v ( t ) ⟹ c 3 = p q = c 1 sin ( p t ) + c 2 cos ( p t ) + c 3 = p ( c 1 cos ( p t ) − c 2 sin ( p t ) ) = − p ( c 1 sin ( p t ) + c 2 cos ( p t ) ) = − p v ( t ) + p c 3 = q = q
Putting v ( t ) = V ( t ) , p = L C 2 , and q = L C E , then V ( t ) = c 1 sin ( L C 2 t ) + c 1 cos ( L C 2 t ) + 2 E .
@Chew-Seong Cheong Thank you so much for figure and solution.
@Chew-Seong Cheong
Can you please show me the steps for solving the above differential equations.
Thanks in advance.
Log in to reply
I have added a note to explain the solving the differential equation. Usually we need to memorize the general solution. Hope that it is useful.
Sorry, but I can't get the answer to Two Inductors . If you can give me. I will provide a solution and rewrite your problem with a figure. Thanks.
Log in to reply
@Chew-Seong Cheong
Thank you so much for adding the note.Answer of Two Inductor is 1.414.
Thanks in advance for posting the solution.
The system equations are:
E − V C = L I ˙ L 1 V C = L I ˙ L 2 I L 1 − I L 2 = C V ˙ C
Subtracting the second equation from the first:
E − 2 V C = L ( I ˙ L 1 − I ˙ L 2 ) = L C V ¨ C
Homogeneous equation:
− 2 V C = L C V ¨ C
This corresponds to simple harmonic motion with angular frequency ω = L C 2 . The general form is:
V C = A cos ( ω t ) + B sin ( ω t ) + D
Apply the following initial conditions to solve for ( A , B , D ) :
V C ( 0 ) = 0 V ˙ C ( 0 ) = 0 V ¨ C ( 0 ) = L C E
After solving for the constants, the final answer is:
V C = 2 E ( 1 − c o s ( ω t ) ) ω = L C 2
I have also included numerical simulation code: