Double Up, Altitudes!

Geometry Level 4

All the altitudes of a triangle is doubled. What is the ratio of the area of the new triangle to the area of the previous triangle?

2 2 2\sqrt2 None of these choices 4 2 4\sqrt2 4 2

View wiki
Emmanuel David by Emmanuel David , 32, Philippines

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

4 solutions

Harsh Khatri
Feb 5, 2016

In △ A B C \bigtriangleup ABC , let A D AD be the altitude from vertex A A to side B C BC .

A D = A B ⋅ cos ⁡ ( ∠ D A B ) = A C ⋅ cos ⁡ ( ∠ D A C ) \displaystyle AD = AB \cdot \cos (\angle DAB) = AC \cdot \cos (\angle DAC)

\text{ }

In the new triangle △ A ′ B ′ C ′ \bigtriangleup A'B'C' , let A ′ D ′ A'D' be the altitude from vertex A ′ A' to side B ′ C ′ B'C' .

\text{ }

A ′ D ′ = 2 × A D A'D' = 2 \times AD while ∠ D ′ A ′ B ′ = ∠ D A B \angle D'A'B' =\angle DAB and ∠ D ′ A ′ C ′ = ∠ D A C \angle D'A'C' = \angle DAC .

\text{ }

A ′ D ′ = A ′ B ′ ⋅ cos ⁡ ( ∠ D A B ) = A ′ C ′ ⋅ cos ⁡ ( ∠ D A C ) \displaystyle A'D' = A'B' \cdot \cos (\angle DAB) = A'C' \cdot \cos (\angle DAC)

\text{ }

⇒ 2 × ( A B ⋅ cos ⁡ ( ∠ D A B ) ) = A ′ B ′ ⋅ cos ⁡ ( ∠ D A B ) \displaystyle \Rightarrow 2 \times (AB\cdot \cos (\angle DAB) ) = A'B' \cdot \cos (\angle DAB)

\text{ }

⇒ 2 × ( A C ⋅ cos ⁡ ( ∠ D A C ) ) = A ′ C ′ ⋅ cos ⁡ ( ∠ D A C ) \displaystyle \Rightarrow 2 \times (AC\cdot \cos (\angle DAC) ) = A'C' \cdot \cos (\angle DAC)

\text{ }

⇒ A ′ B ′ = 2 × A B \displaystyle \Rightarrow A'B' = 2 \times AB

⇒ A ′ C ′ = 2 × A C \displaystyle \Rightarrow A'C' = 2 \times AC

\text{ }

Similarly, we can prove B ′ C ′ = 2 × B C B'C' = 2 \times BC .

A r e a ( △ A B C ) = A B ⋅ A C ⋅ sin ⁡ ( ∠ B A C ) 2 \displaystyle Area(\bigtriangleup ABC) = \frac{AB\cdot AC \cdot \sin (\angle BAC)} {2}

A r e a ( △ A ′ B ′ C ′ ) = A ′ B ′ ⋅ A ′ C ′ ⋅ sin ⁡ ( ∠ B ′ A ′ C ′ ) 2 \displaystyle Area(\bigtriangleup A'B'C') = \frac{A'B'\cdot A'C' \cdot \sin (\angle B'A'C')} {2}

\text{ }

A r e a ( △ A ′ B ′ C ′ ) A r e a ( △ A B C ) = A ′ B ′ ⋅ A ′ C ′ A B ⋅ A C \displaystyle \frac{Area(\bigtriangleup A'B'C')} {Area(\bigtriangleup ABC)} = \frac{A'B' \cdot A'C'} {AB \cdot AC}

\text{ }

⇒ A r e a ( △ A ′ B ′ C ′ ) A r e a ( △ A B C ) = 4 \displaystyle \Rightarrow \frac{Area(\bigtriangleup A'B'C')}{Area(\bigtriangleup ABC)} = \boxed{4}

4 Helpful 0 Interesting 0 Brilliant 0 Confused

There is an obscure formula on finding the area of a triangle given all the altitudes. That is A 1 = 1 ( 1 h a + 1 h b + 1 h c ) ( − 1 h a + 1 h b + 1 h c ) ( 1 h a − 1 h b + 1 h c ) ( 1 h a + 1 h b − 1 h c ) \displaystyle A_1 = \frac{1}{\sqrt{(\frac{1}{h_a} + \frac{1}{h_b} + \frac{1}{h_c})(-\frac{1}{h_a} + \frac{1}{h_b} + \frac{1}{h_c})(\frac{1}{h_a} - \frac{1}{h_b} + \frac{1}{h_c})(\frac{1}{h_a} + \frac{1}{h_b} - \frac{1}{h_c})}} where a , b \displaystyle a, b and c \displaystyle c are the sides and h a , h b \displaystyle h_a, h_b and h c \displaystyle h_c are their corresponding altitudes, respectively. Thus, when doubling the respective heights, we have A 2 = 1 ( 1 2 h a + 1 2 h b + 1 2 h c ) ( − 1 2 h a + 1 2 h b + 1 2 h c ) ( 1 2 h a − 1 2 h b + 1 2 h c ) ( 1 2 h a + 1 2 h b − 1 2 h c ) \displaystyle A_2 = \frac{1}{\sqrt{(\frac{1}{2h_a} + \frac{1}{2h_b} + \frac{1}{2h_c})(-\frac{1}{2h_a} + \frac{1}{2h_b} + \frac{1}{2h_c})(\frac{1}{2h_a} - \frac{1}{2h_b} + \frac{1}{2h_c})(\frac{1}{2h_a} + \frac{1}{2h_b} - \frac{1}{2h_c})}} ⟹ A 2 = 1 1 16 ( 1 h a + 1 h b + 1 h c ) ( − 1 h a + 1 h b + 1 h c ) ( 1 h a − 1 h b + 1 h c ) ( 1 h a + 1 h b − 1 h c ) \displaystyle \Longrightarrow A_2 = \frac{1}{\sqrt{\frac{1}{16}(\frac{1}{h_a} + \frac{1}{h_b} + \frac{1}{h_c})(-\frac{1}{h_a} + \frac{1}{h_b} + \frac{1}{h_c})(\frac{1}{h_a} - \frac{1}{h_b} + \frac{1}{h_c})(\frac{1}{h_a} + \frac{1}{h_b} - \frac{1}{h_c})}} ⟹ A 2 = 1 1 4 ( 1 h a + 1 h b + 1 h c ) ( − 1 h a + 1 h b + 1 h c ) ( 1 h a − 1 h b + 1 h c ) ( 1 h a + 1 h b − 1 h c ) \displaystyle \Longrightarrow A_2 = \frac{1}{\frac{1}{4}\sqrt{(\frac{1}{h_a} + \frac{1}{h_b} + \frac{1}{h_c})(-\frac{1}{h_a} + \frac{1}{h_b} + \frac{1}{h_c})(\frac{1}{h_a} - \frac{1}{h_b} + \frac{1}{h_c})(\frac{1}{h_a} + \frac{1}{h_b} - \frac{1}{h_c})}} ⟹ A 2 = 4 ( 1 h a + 1 h b + 1 h c ) ( − 1 h a + 1 h b + 1 h c ) ( 1 h a − 1 h b + 1 h c ) ( 1 h a + 1 h b − 1 h c ) \displaystyle \Longrightarrow A_2 = \frac{4}{\sqrt{(\frac{1}{h_a} + \frac{1}{h_b} + \frac{1}{h_c})(-\frac{1}{h_a} + \frac{1}{h_b} + \frac{1}{h_c})(\frac{1}{h_a} - \frac{1}{h_b} + \frac{1}{h_c})(\frac{1}{h_a} + \frac{1}{h_b} - \frac{1}{h_c})}} Obvioulsly, the new area is multiplied by 4 4 and thus, the desired ratio is 4 : 1 \displaystyle 4:1 or 4 \displaystyle 4 .

For more information on how to get that formula, click this .

Reineir Duran - 5 years, 4 months ago

Log in to reply

That's exactly how I formulated my problem. We have the same source also. Nice one

Emmanuel David - 5 years, 4 months ago

Can you please post it as another solution. Thanks :)

Emmanuel David - 5 years, 4 months ago

Log in to reply

Actually, seeing the problem, I did clicked for the solution immediately since I wanted to discover something new on the solution section . Posting the solution is now prohibited.

Reineir Duran - 5 years, 4 months ago

Log in to reply

@Reineir Duran – Ahhh okay :)

Emmanuel David - 5 years, 4 months ago

Cool, but is it a common knowledge that when you double the altitudes, the sides are also doubled?

Emmanuel David - 5 years, 4 months ago

Log in to reply

I think so. As we are doubling the altitude the triangle is dilated. The new triangle is similar to the original triangle. Also on the basis of similarity conditions Side ratio = altitude ratio. Thus side of the new triangle is double the side of original triangle.

ADARSH KRISHN - 5 years, 4 months ago

But with a little bit of logic, we can apply similarities on both of the triangles, the original and the new one. The altitudes are doubled up, that's why the area of the new triangle formed should be then multiplied by 4 4 .

Reineir Duran - 5 years, 4 months ago

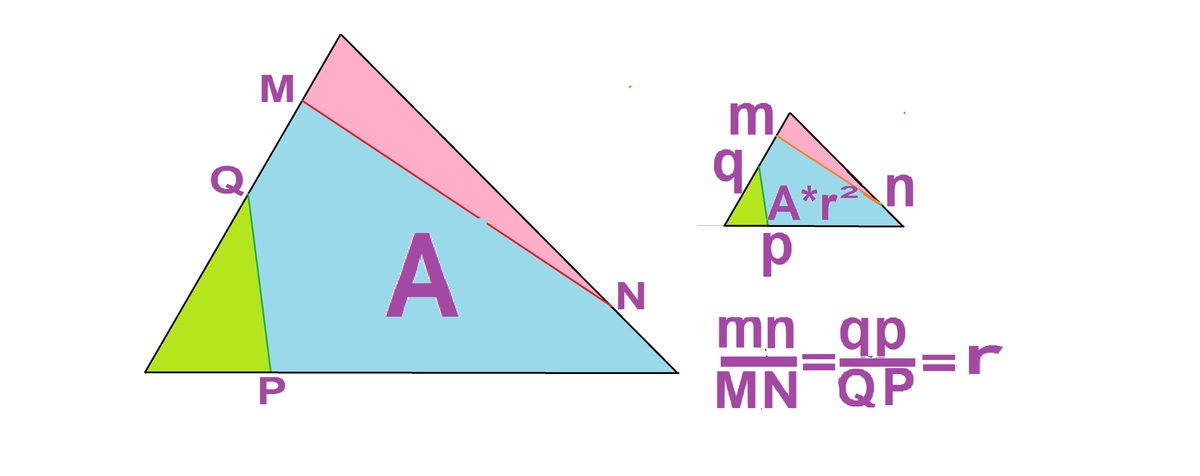
First, if all three altitudes are increased or decreased by a ratio R, the area is also changed by a ratio of R 2 R^2 . So in our case it is 4. And the triangles are similar. In fact, if there are two similar triangles, and on one, MN and PQ are segments, M on one side, N on another, P on the third side and Q on any of the remaining. mn and pq are similarly placed on the other triangle. The ratio R= M N m n = P Q p q , \dfrac{MN}{mn}=\dfrac{PQ}{pq}, then the ratio of their areas is R 2 R^2 .

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Andreas Wendler
Feb 9, 2016

Since validity is given for all triangles so simply choose a right-angle one. Because the sides beside the right angle representing two heights will double so in product the area will be the 4th.

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Pulkit Gupta
Feb 7, 2016

Lets go elementary.

Consider a right angled triangle with base of length x and height y. The area then is 1 2 x y \large \frac{1}{2}xy .

Now if we double up the base and height ( which are actually the altitudes of the right angled triangle) we obtain an area 4 times the previous.

Hence, the answer.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...