Find the Maximum Product!

This is a solution from first principles, that doesn't require the AM-GM theorem (although, this is a great AM-GM problem).

In summary: this algebra problem describes a geometric situation: "If a rectangular prism has a fixed total length of edges, what dimensions maximize the volume?" The solution is a cube, just like how, in two dimensions, if you have a fixed perimeter, the square is the most efficient way to entrap area.

This problem is awesome -- it lines up with our intuition that $a, b,$ and $c$ should be treated symmetrically. You can read on for a deeper dive into these details.

NOSTALGIA

Remember the lab that you did in elementary or middle school, making all of the rectangles that have unit-side-lengths and a fixed total perimeter and comparing the areas.

You find that the long thin rectangles are very inefficient of course and that the square is the most efficient. But why?

PROOF THAT SQUARES ARE THE BEST

Here's a solid explanation of why squares are the most efficient rectangles for containing area. Let $x$ and $y$ be the dimensions of the rectangle. By fixing the perimeter, say to $2C$ you're guaranteeing that the perimeter $= 2x+ 2y = 2C \rightarrow x+y=C$ . Therefore $y=C-x$ and so, substituting to find the area: $Area = xy = x(C-x) = -x^2 + Cx$ . This is a quadratic expression that looks something like this green curve (a frown):

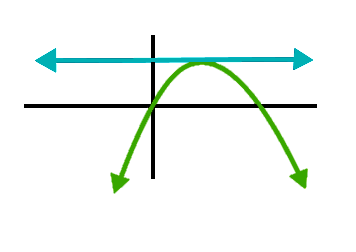
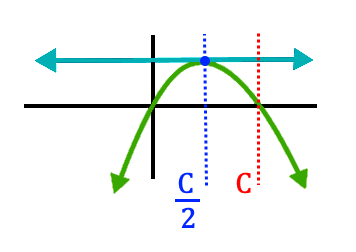
And therefore it has one maxima that is at the $x$ -value directly between the equation's two roots. Factoring $0=-x^2 + Cx = x (-x+C)$ , we get that the two roots are $x=0$ and $x=C$ . Therefore, the maxima occurs at $x=\frac{C}{2}$ , and that's our conclusion: to maximize $C=xy$ , choose $x=y=\frac{C}{2}$ .

PROOF THAT CUBES ARE THE BEST

But the given problem has 3 variables, not two, so we are not yet finished. And yet if you know and trust the fact now, that a square is the most efficient area-trapping rectangle given a fixed perimeter, then this problem is simply the 3-dimensional analog. If you believe this fact in 2D, 3D comes naturally.

Given that the total length of all edges of a rectangular prism added together ( $4l+4w+4h$ ) is fixed, what choice of $l, h, \text{and} w$ maximize the volume, $lhw$ of the rectangular prism.

Proving that a cube is most efficient is a simple matter if you trust that a square is most efficient in 2D. Just imagine that for some strange reason, a non-cubic rectangular prism holds more area than a cube. A non-cubic rectangular prism would have at least 4 non-square faces. Choose one of those faces, say, without loss of generality, that it's a $l \times w$ face. Then without changing $h$ , we can trade length between $l$ and $w$ until they are equal, strictly increasing the area of the $l \times w$ face, and therefore, since $h$ is fixed, the area of the rectangular prism. Therefore, there's no reason for any side of the most efficient volume-containing rectangular prism to be anything but a square. Therefore, the most efficient rectangular prism is a cube.

OUR SPECIFIC CASE

That's why, in this case, with $l + w + h$ fixed as 6, and therefore the sum total of edges $4l +4w + 4h = 4(l+h+w)$ fixed as 24, the way to maximize the volume, $lhw$ is to make $l=w=h=2$ . Therefore $lhw=8$ .

Given that,

$a + b + c = 6 \quad,\quad a + b + c = 3\times 2\quad,\quad \frac{a + b + c}{3} = 2$ By Applying the Arithmetic Mean Geometric Mean Inequality , we have $AM\ge GM$ , for maximum value of GM, AM = GM.

Therefore, $\frac{a + b + c}{3} = \sqrt [ 3 ]{ abc } \quad,\quad 2=\sqrt [ 3 ]{ abc }$ Hence, the maximum value is $\boxed {abc = 8}$ .

By AM-GM, $\frac{a+b+c}{3} \geq \sqrt[3]{abc}$

$a+b+c=6$ , so $\frac{a+b+c}{3}=2$

$2 \geq \sqrt[3]{abc}$

$8 \geq abc$

So our answer is $\fbox{8}$ .

Out of 10 possible sets of solutions, (1,14),(1,2,3),(1,3,2).......(4,1,1)

only (2,2,2) will give maximum product value=8

Given, a+b+c=6, there are 3 numbers. Also given that value is maximum, value of 1 number = $\frac{6}{3}$ = 2.

abc = 2x2x2 = 8

To product to be max the numbers must be equal Therefore given sum is a+b+c=6 a=b=c=2 Therefore abc=2 2 2=8

a x b x c = 8

To product to be max the numbers must be equal Therefore given sum is a+b+c=6 a=b=c=2 Therefore abc=222=8

I don't know if i'm missing somethng here but what about 3,3,0 that would give us 9 as the maximum, I still count zero as a positive number

For minimum... a=b=c

by symmetry, the product will be maximum when a = b = c . Thus, abc = 2 x 2 x 2 = 8

a+b+c= 6 6+2=8

$a + b + c = 6$

Based on AM $\ge$ GM

$\frac { a+b+c }{ 3 } \ge \sqrt [ 3 ]{ abc }$

$\frac { 6 }{ 3 } \ge \sqrt [ 3 ]{ abc }$

$2\ge \sqrt [ 3 ]{ abc }$

$8\ge abc$

So, the maximum value is $8$ .

Why can't a or b or c be 1? The maximum possible would be 9.