AMC problem
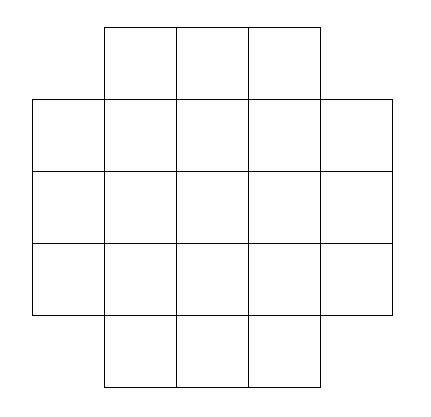
A square has side length 5. A 1 by 1 square is cut from each corner. What is the area of the largest possible inscribable square?
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Thanks. I'm not sure how to do a diagram. Could you explain?
Log in to reply
I added an image for you. Could you use it to improve your presentation?
Log in to reply
Sir, I have given wrong answer, so I can't really give a solution, please update this solution in his solution.
Now as
1
×
1
squares are cut off from each sides, obviously one big
3
×
3
can be formed. Now as this question asks for the largest possible area, we draw one triangle on each of its four sides as shown in the picture. The area of these
4
triangles would be
4
×
2
1
×
base
×
height
=
2
×
3
×
1
=
6
So, the total area is ( 3 × 3 ) + 6 = 1 5 c m
Log in to reply
@Ashish Menon – so simple and yet ... i hate these when it makes you feel like an incompetent person. grr ;)
@Ashish Menon – How do you get the base to be3
Yes, thank you. I'm a little rushed but I'll improve my explanation tomorrow. Could you explain how to add a picture in the future?
Log in to reply
@Sal Gard – When you publish / edit a problem or solution, you see a formatting toolbar. Click on the image picture (circled in red) and you will be asked to select a file to upload. We then do what is needed, to display a picture where your cursor is located. You can copy the markdown code and move it to another position if needed.
This solution is not clearly phrased enough for someone who doesn't know how to solve the problem to read it an understand it immediately. I advise you to add a diagram to make it clear what you are saying.
Plz explain, I really didnt understand.
A proof is missing to show that the 4 added triangles are rightangles!
Log in to reply
Why should they be right triangles?
Log in to reply
To form a square!
Log in to reply
@Andreas Wendler – Great observation
Log in to reply
@Ashish Menon – Impossible for you probably! If you were able to do you should be able to define were the tops of the added triangles are located. I don't think so ;-(( - but I can!!!
Hi Andreas, If you draw a circle (centered at the center of the inscribed circle) and passing through the 4 points of the inscribed square (of area 15), the opposite points of the inscribed square will generate a diameter of the circle. A triangle inscribed in a semicircle is a right triangle. That should take care of that part of the proof.
The distance of the vertex of the right angle triangle(violet) from one side is (3+√5)/2 and from other side is (3-√5)/2. This isn't the middle point of the side of a unit length square.
It doesn't need to be the middle point of a unit length square. In fact, the area is usually minimized and in this case doesn't even work.
Looking at the area of a three by three square, we get nine. To get the largest possible area, we add four triangle that would touch the sides. Each has area 3*1/2=1.5. Therefore total area is 9+6=15.