Ampere's Law Exercise (Part 3) - "A bit" less calculus
An infinitely long straight wire carries 1 unit of electric current. The wire is perpendicular to the x y plane, and passes through the point ( x , y ) = ( 2 1 , 0 ) . Consider an integration path consisting of a circle of radius 1 in the x y plane with its center at ( x , y ) = ( 0 , 0 ) . Define the following magnetic line integrals over the "left" ( x ≤ 0 ) and "right" ( x > 0 ) halves of the integration path:
Q L = ∫ x ≤ 0 B ⋅ d ℓ Q R = ∫ x > 0 B ⋅ d ℓ
In the above integrals, B is the vector magnetic flux density produced by the wire at a particular point. Determine the following ratio:
Q L + Q R Q R
Details and Assumptions:
1)
Magnetic permeability
μ
0
=
1
2)
You know ahead of time what the denominator of the ratio is
3)
Use the same circulation (clockwise or counter-clockwise) when evaluating both integrals
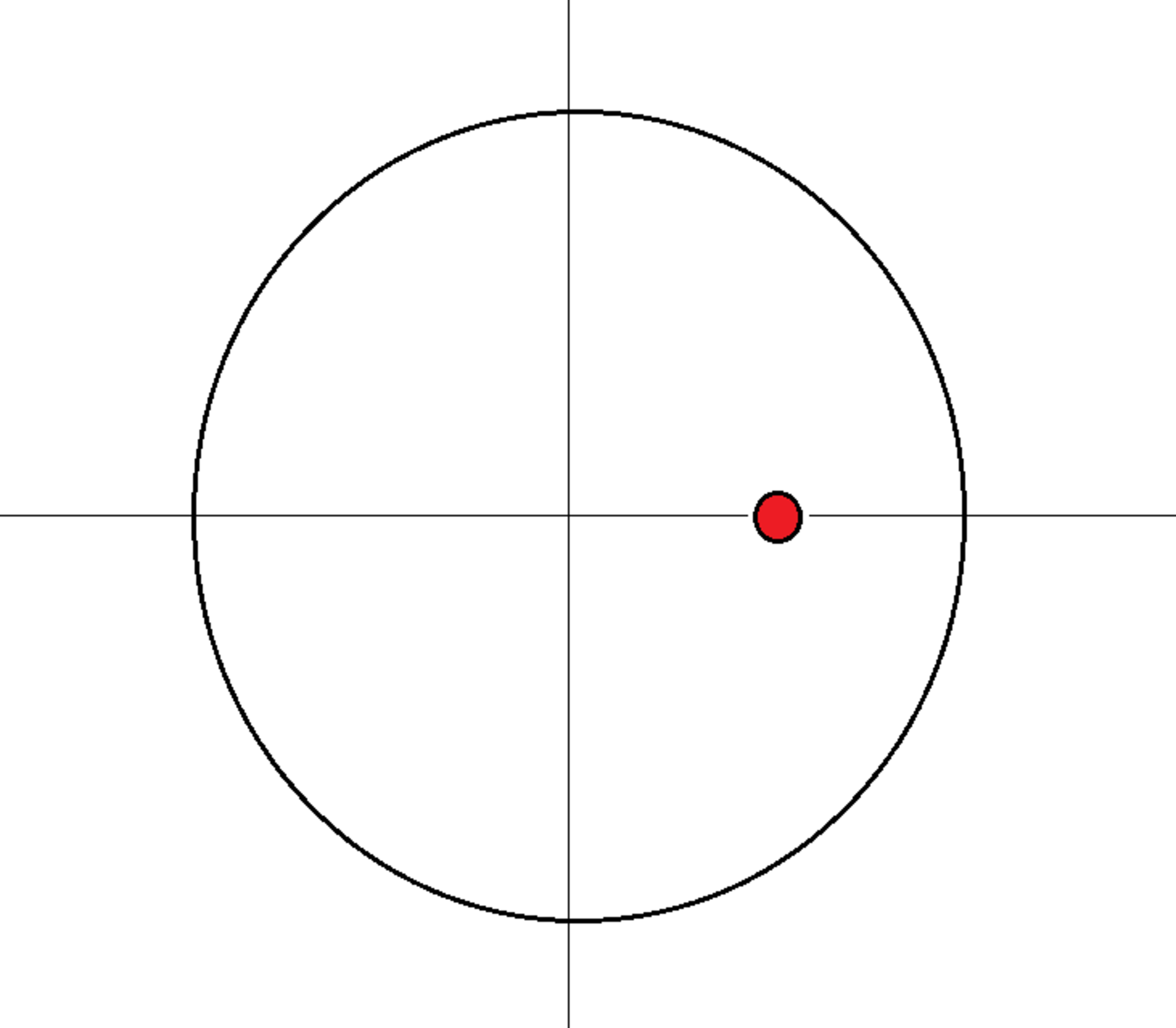
The answer is 0.6476.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
@Karan Chatrath Sir I have solution of this question and I have wrong answer but by different method. I am not able to understand why my answer is coming wrong.Should were I post my solution so that you can find mistake??? Please
Log in to reply
You can paste a snapshot of your work or type out your solution as a comment in this thread.
Log in to reply
@Karan Chatrath can you help me finding mistake in my method?? Please
Log in to reply
@A Former Brilliant Member – In your 4th snapshot, you copied the value of b from the previous snapshot incorrectly. I have not looked beyond this.
In snapshot 3 you get:
b = π ( 5 − 4 cos θ ) 1 − 2 cos θ
At the beginning of snapshot 4 you re-write b as:
b = π ( 5 − 4 cos θ ) 1 − 2 sin θ
Log in to reply
@Karan Chatrath – Oh Yeah that's the mistake.
Log in to reply
@A Former Brilliant Member – @Karan Chatrath After correction I got the correct answer. Thank you sir
Key steps of the problem are highlighted. Consider the position vector of a point P on the circular loop:
r p = cos θ i ^ + sin θ j ^ d r p = ( − sin θ i ^ + cos θ j ^ ) d θ
The position vector of the location of the wire in the X-Y plane (Named C ) is:
r p = 0 . 5 i ^
A vector joining point C and P and directed towards P is:
r = r p − r c
The magnetic field at point P due to the infinite wire is (assuming current flows into the plane of the paper):
B = 2 π ∣ r ∣ μ o I ( − k ^ × r ^ )
Having obtained B , the next step is to calculate the following dot product:
d Q = B ⋅ d r p
Finally, all expressions are substituted and the resulting expression is:
d Q = π μ o I ( 5 − 4 cos θ cos θ − 2 ) d θ
The working is left out in this solution. Finally,
Q R = π μ o I ∫ − π / 2 π / 2 ( 5 − 4 cos θ cos θ − 2 ) d θ
Q L + Q R = π μ o I ∫ 0 2 π ( 5 − 4 cos θ cos θ − 2 ) d θ = − μ o I
The second integral verifies Ampere's law. The closed-form expressions are evaluated (working left out) and the required ratio evaluates to:
Q R + Q L Q R = 4 π 4 arctan 3 + π ≈ 0 . 6 4 7 5 8 3 6