This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
but how u know that (x-13) is common
Log in to reply
13 is a factor of 2002. You have to find it out by try and error. I actually cheated. I plot the curve using a spreadsheet and found the root is 13.
Ok please find anathor method
how to simplify a 3rd degree polynomial into 3 first degree polynomials or 1 first degree and 1 second degree polynomial .. pls help me anyone
Log in to reply
We can use Rational Roots (or Zeros) text. Let f ( x ) = x 3 − x 2 − 2 x − 2 0 0 2 . We note that 2 0 0 2 = 2 × 7 × 1 1 × 1 3 . We test and see if x − 2 , x − 7 , x − 1 1 and x − 1 3 are factors of f ( x ) . In this case f ( 1 3 ) = 0 , therefore, x − 1 3 is a factor. The other factor is found by dividing f ( x ) by x − 1 3 . Please note that not all polynomials can be factorized.
Log in to reply
thnx... is there any general method to factorize 3rd degree polynomials?
Log in to reply
@Anand O R – No, other ways, usually you use Rational Roots Test. You may want to know about Cardano's cubic formula ( more... ).
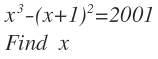
x 3 − ( x + 1 ) 2 = 2 0 0 1
⇒ x 3 − x 2 − 2 x − 2 0 0 2 = 0
( x − 1 3 ) ( x 2 + 1 2 x + 1 5 4 ) = 0
The only real root is x = 1 3 .