An Ancient Chinese Puzzle

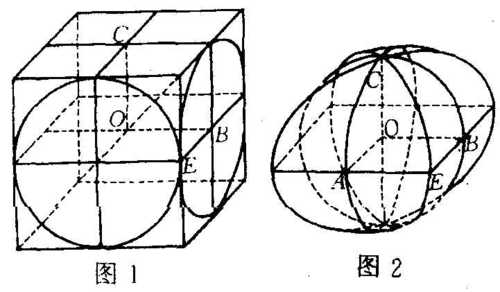There is a quick solution involving Cavalieri's Principle. In fact, the Chinese mathematician Liu Hui in the 3rd century showed this exact ratio by noting that each cross-section is a circle inscribed in a square! Hence the ratio of the bulk solid follows 4/pi.

I have used co-ordinate geometry to tackle this problem. I have assumed two cylinders with the equations ${ x }^{ 2 }+{ y }^{ 2 }\le { r }^{ 2 }\quad and\quad { y }^{ 2 }+{ z }^{ 2 }\le { r }^{ 2 }$ representing cylinders with axis along the $z$ -direction and $x$ -direction respectively. We have to find the volume of the resultant figure.

As we do in the case of sphere we assume it to be composed of infinite non circular disks of infintesimal thickness.

So at co-ordinate z we have a thin non-circular disk of thickness dz and the shape of the disk is as shown in the figure.

Image

$k=\sqrt { { r }^{ 2 }-{ z }^{ 2 } }$

$dV=area(shaded \quad region)dz$

$Area \quad shaded\quad region = 2area(sectorBOD)+4area(BEO)$

$=2\times OE\times OB+2{ r }^{ 2 }\cos ^{ -1 }{ \frac { BE }{ OB } }$

$dV=2(z\sqrt { { r }^{ 2 }-{ z }^{ 2 } } +{ r }^{ 2 }\cos ^{ -1 }{ \frac { z }{ r } } )dz$

$V=2(\int _{ 0 }^{ r }{ dV })=4(\int _{ 0 }^{ r }{ z\sqrt { { r }^{ 2 }-{ z }^{ 2 } } +{ r }^{ 2 }\cos ^{ -1 }{ \frac { z }{ r } } dz })$

Solving ${ V }_{ figure }=\frac { 16{ r }^{ 3 } }{ 3 }$

also ${ V }_{ sphere }=\frac { 4\pi { r }^{ 3 } }{ 3 }$ so our volumetric ratio is :

$\boxed {\frac { { V }_{ Figure } }{ { V }_{ Sphere } } =\frac { 4 }{ \pi } }$

I performed this problem as student in the tedious way but the straight forward method is the one mentioned above by Steven Zheng .

Indeed years later I found this problem on the front cover of Martin Gadner Book its title is " The Unexpected Hanging and Other Mathematical Diversions " I bought it and saw inside it was solved in the same fashion that the one by the Chinese mathematician.

using the prismoidal formula: V = L/6 * (A1 + 4Am + A2). Lenght will be twice the radius of the cylinder. A1 is the area at point C, Am is the area at horizontal plane O which the square of 2R. and A2 is the area at the bottom point. therefore, V = (2R/6) * [ 0 + 4(2R)^2 + 0 ] = 16/3 R^3. finding its ratio from the volume of a sphere which is 4/3 pi*R^3, will give the ratio 4/pi or 1.273