An Ancient Number System
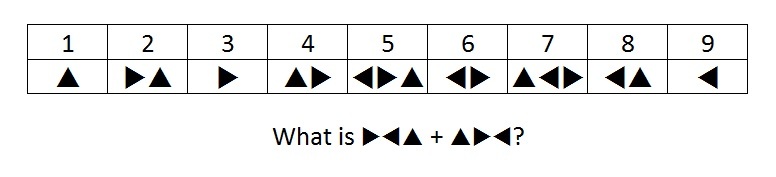
You have been asked to consult on a recently discovered ancient number system. So far, archaeologists have found examples of some symbols associated with expressing quantities. These symbols are ▲, ►, and ◄.
With that information, they have been able to link combinations of these symbols to certain quantities. Their results are in the table above.
Recently, they have found combinations of these symbols referencing two unknown quantities: ►◄▲ and ▲►◄.
What is the sum of the two unknown quantities above?
The answer is 24.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Number Base - Problem Solving
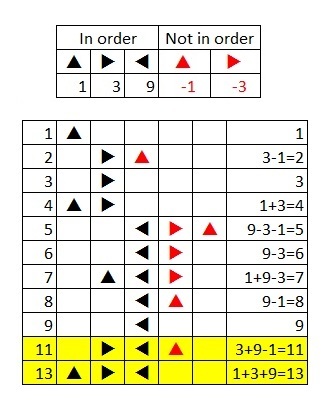
The symbols and ◄, ► and ◄ are valued at 1, 3 and 9, respectively. We should first notice that no symbols are ever *reused * in any of these combinations. This leads us to consider that this isn't just a case of simple base conversion.
However, perhaps these symbols are some combination of sums and differences. Since 2 = ►▲= 3 - 1 we can start by guessing that placing a symbol after another results in subtraction. 6 =◄► = 9 - 3 and 8 = ◄▲ = 9 - 1 help confirm that conjecture. As well, since 4 =▲►= 3 + 1 we can infer that placing a symbol before another results in addition.
More complicated combinations will require more complicated rules. For instance:
5 = ◄►▲ = 9 - 3 - 1 follows only the "subtraction after" rule (assuming 9 is the "start") ≠ 9 + 3 - 1 breaks both the "subtraction after" and "addition before" (assuming 3 is the "start") ≠ 9 - 3 + 1 not ≠ 9 + 3 + 1 breaks the "addition before" rule (assuming 1 is the "start")
7 = ▲◄► = 1 + 9 - 3 follows both the "subtraction after" and "addition before" (assuming 9 is the "start") ≠ 1 - 9 - 3 breaks the "subtraction after" rule (assuming 1 is the "start") ≠ 1 - 9 + 3 ≠ 1 + 9 + 3 breaks the "addition before" rule (assuming 3 is the "start")
In both cases, the largest quantity in the combinations (9 = ◄) determined the "starting point" of the operational precedence. Taking the same approach with our unknown sequences:
►◄▲ = 3 _ 9 _ 1 => by following both the "subtraction after" and "addition before" rules (assuming 9 is the "start") we get 3 + 9 - 1 = 11 and ▲►◄ = 1 _ 3 _ 9 => by following only the "addition before" rule (assuming 9 is the "start") we get 1 + 3 + 9 = 13
And so, the resulting sum is 11 + 13 = 24
This problem was inspired by the "Minimum Set of Weights Puzzle" . I envisioned a society that wrote numbers as they would appear as representations of a result of differential weights in a simple pan balance.
These rules also leads to some "degenerate" combinations such as: ►▲◄ = 3 _ 1 _ 9 = 3 - 1 + 9 (same as 11 = ►◄▲)
Interestingly, another degenerate combination is: ◄▲► = 9 _ 1 _ 3 = 9 - 1 + 3 also "yielding" 11.
I'd be keen to see if anyone is interested in helping work out some of these issues. As I mentioned, "more complicated combinations will require more complicated rules". For instance, using 27 = ▼, we can extend the table all the way to 40:
Some degenerate 4-term combinations include:
Finally, his system is also related to (but distinctly different from) "balanced ternary" notation.I only mention this because I'd like to call these "balance numbers", but don't want to confuse them with the concept above.