Current crossing the bridge
If I = 1 2 A , E = 5 V , R = 7 Ω in the circuit below, find the current I X in ampere flowing through the resistor in the middle. All the elements of the circuit are ideal.
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
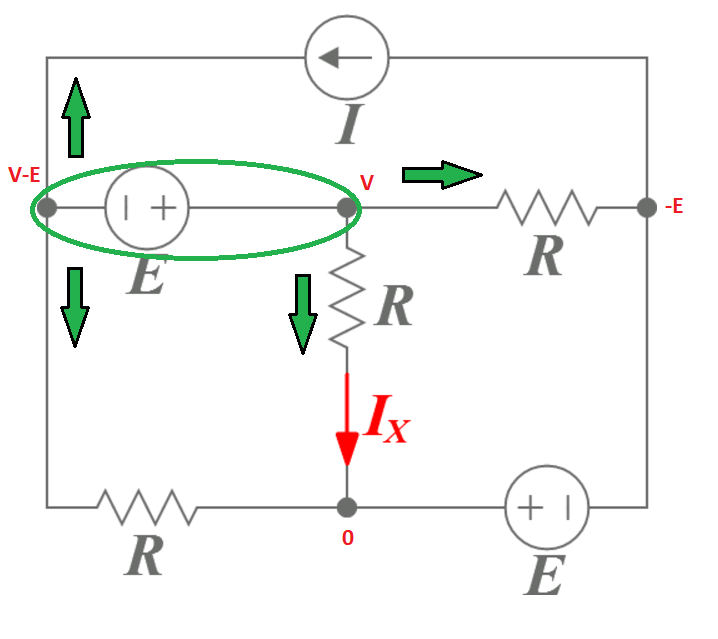
Step 1
- Create a "super node" as shown by the green ellipse. The sum of the currents out of this must be zero.
Step 2
- Symbolically label the node voltages as shown
Step 3
- Write an expression for the total current flowing out of the "super node"
R V − E − I + R V + R V + E = 0 V = 3 I R I X = R V = 3 R I R = 3 I = 4
Interestingly, we don't actually need the numerical value of E or R .
@Steven Chase Sir , isn't the situation like two variables and three equations? (Three loops - Kirchoff's rules and only two unknowns )
Log in to reply
IX is just a scaled version of what I call V, so I think there is effectively only one unknown. You can use whatever procedure you like, as long as you are consistent.
Log in to reply
The results that I am getting is inconsistent ...(Assuming the value of Ix to be 4
Loop law in the right bottom small loop - 2 8 − 7 i + 5 = 0 ⇒ i = 3 3 / 7 , loop law in the uppermost loop 5 − 7 i = 0 ⇒ i = 5 / 7
Please help me spot the error.
Log in to reply
@Ankit Kumar Jain – The current through the rightmost resistor is 33/7 (flowing to the right). The current through the middle resistor is 4 (flowing down). The current in any branch is a superposition of loop currents.
Log in to reply
@Steven Chase – Yes the current in the rightmost resistor comes out to be 33/7 when loop law is being applied in the rightmost loop but it gives a value of 5/7 when loop law is being applied in the topmost loop...
Log in to reply
@Ankit Kumar Jain – If we take for granted (based on previous analysis) that V = 28, we can then start with 12 amps flowing into the left node. Then we have 12 - 23/7 - 28/7 = 33/7
The problem can be solved very easily by using the method of superposition. The goal is to determine how each of the current or voltage sources affect the current we're looking for. It works this way:
There is one current source and two voltage sources, so we have three cases:
Given the above rules, we have that: I X = I X 1 + I X 2 + I X 3 Take a look at the first case. We can rearrange it this way: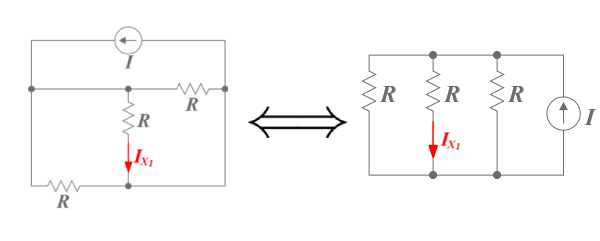 So, we have three identical resistors connected in parallel to the current source, which means that the current flowing from the source will be split into three equal parts. Thus:
I
X
1
=
3
I
So, we have three identical resistors connected in parallel to the current source, which means that the current flowing from the source will be split into three equal parts. Thus:
I
X
1
=
3
I
Now, take a look at the second and the third case. Notice that you get the third case if you rotate the second case by 180°. It means that second and third case yield currents of equal intensities that flow in opposite directions - so they cancel each other out: I X 2 = − I X 3
Having all this in mind, we finally have that : I X = I X 1 + I X 2 + I X 3 = I X 1 = 3 I = 4 A .