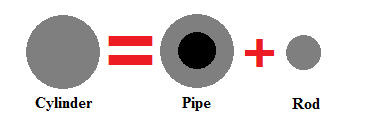
Cylinder $=$ pipe $+$ rod

Electricity and Magnetism Level 3

Consider an iron cylinder, which is divided to extract a rod and a pipe, whose resistances are equal.

Find $\dfrac{R_\text{cylinder}}{R_\text{rod}}$ .

Details and Assumptions :

$R_\text{cylinder}=$ Cylinder's radius.

$R_\text{rod}=$ Rod's radius.

The answer is 1.4142.

1 solution

Paola Ramírez
Feb 17, 2016

Its resistance are the same if its areas are iqual, so pipe's area $=$ rod's area.

Pipes's area is $(R^2_\text{cylinder}-R^2_\text{rod})\pi$

Rod's area is $(R^2_\text{rod})\pi$

$(R^2_\text{cylinder}-R^2_\text{rod})\pi=(R^2_\text{rod})\pi \Rightarrow R^2_\text{cylinder}=2r^2_\text{rod} \therefore \boxed{\frac{R_\text{cylinder}}{R_\text{rod}}=\sqrt{2}}$

One can also do this by equating volume of the rod and pipe.

Akshat Sharda - 5 years, 3 months ago

Though you got a correct answer by equating volume, but it's a wrong concept.

Akhil Bansal - 5 years, 3 months ago

Since R = $\frac{\rho L^2}{AL}$ , where AL is the volume of the resistor ; provided the length is constant for both ( which in this case is), Akshat's method is absolutely correct :-)

Pulkit Gupta - 5 years, 3 months ago

Then what is the right thing ?

Akshat Sharda - 5 years, 3 months ago

@Akshat Sharda – Resistance of both the wires is same.
$\large R = \dfrac{\rho l}{A}$ Resistivity and length of both of them are same. Hence, we'll compare their areas and not the volume.

Akhil Bansal - 5 years, 3 months ago

I think no concept of magnetism is used.(your problem's title)=

Akhil Bansal - 5 years, 3 months ago

Does we could use the area of the pipe to be perimeter of the cylinder multiplied by thickness

Vivek Singh - 2 months, 2 weeks ago

Cylinder = = = pipe + + + rod

The answer is 1.4142.

1 solution

0 pending reports

Cylinder $=$ pipe $+$ rod