An electricity and magnetism problem by Rishabh Deep Singh
Find the RMS value of to the truncated nearest integer.
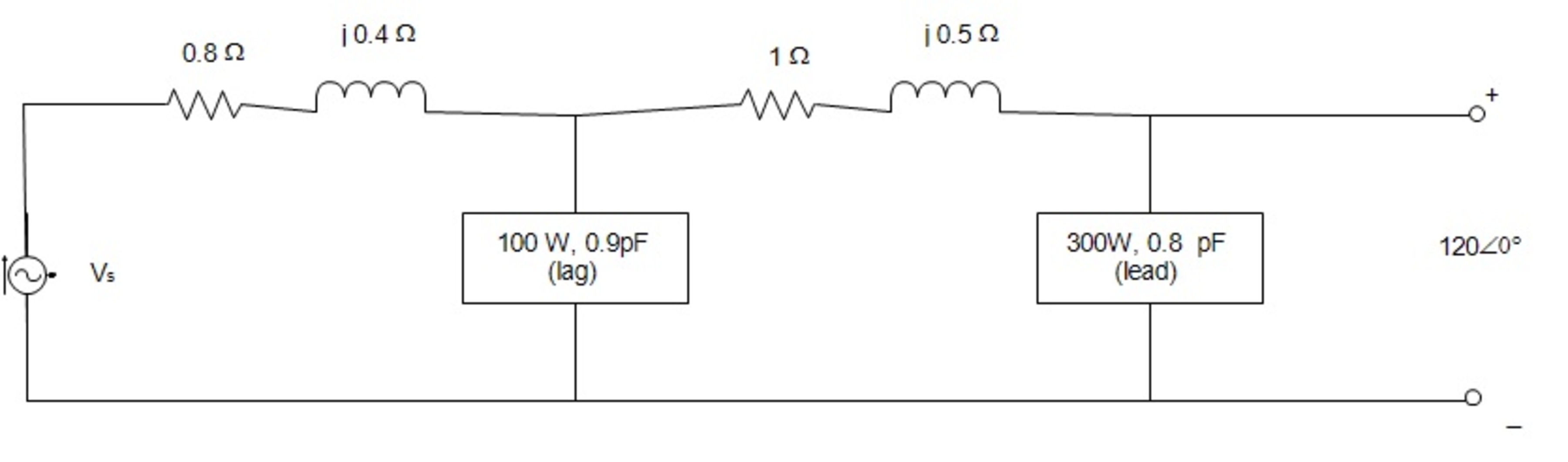
Clarification .
The answer is 123.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
This is a cool problem. It relies heavily on complex power analysis principles, the full scope of which is too large to cover here. The biggest things to consider are the following:
1) The complex power (active power (P) + j * reactive power (Q)) through a load, as a function of the voltage and current through it is:
S = P + j Q = V I ∗
Where I ∗ is the complex conjugate of I
2) A load with leading power factor (capacitive) behaves as a reactive power source, and thus it consumes negative reactive power.
3) A load with lagging power factor (inductive) behaves as a reactive power sink, and thus it consumes positive reactive power.
Here is a sketch of my solution (programmed in Mathcad). I think the problem should state more clearly that it is looking for the RMS magnitude of the source voltage, truncated to the nearest integer (which turns out to be 123). @Rishabh Deep Singh , can you make this more clear?