An equilateral triangle

The locus of points traced out by $C$ all lie on a circle that circumscribes an equilateral triangle with $AB$ as a base.

This is because, in a circle, inscribed angles that intercept the same arc (namely $AB$ ) are congruent (in this case all equal to $60^\circ$ ).

Since $C$ is chosen above the $x$ axis, the path traced out by all possible values of $C$ will include $\frac{2}{3}$ of that circumference (the part of the circle above the $x$ axis).

Since $AB = 1$ , the radius of the circumscribed circle will be

$R = \dfrac{AB}{\sqrt{3}} = \dfrac{1}{\sqrt{3}}$

So, the circumference of the circle will be given by:

$C = 2\pi R = \dfrac{2\pi}{\sqrt{3}}$

So, the portion that $C$ traces out will be:

Length $= \dfrac{2}{3}C = \dfrac{4\pi}{3\sqrt{3}} = \boxed{2.42}$ to two decimal places.

Now for the more challenging 3D version of this question... What is the area of the locus of points traced out by a vertex of a tetrahedron, where all three edges intersecting at that vertex lie on a unit circle? :0)

My initial approach was the same as Geoff's, using the fact that the inscribed angle's measure is half of the measure of the intercepted arc. (Generalization of Thales' Theorem.) Just for fun, here is an alternative solution using vectors.

---

$A$ , $B$ , $C$ lie on two different sides of an equilateral triangle iff the vectors $\vec{AC}$ and $\vec{BC}$ make a $60^\circ$ angle. That is, $\vec{AC}\cdot \vec {BC} = \cos 60^\circ| |\vec {AC}|\ |\vec{BC}|.$ Substitution $\vec A = (-\tfrac12,0),\ \vec B = (\tfrac12,0),\ \vec C = (x,y)$ this means x\cdot(x-1) + y\cdot y = \tfrac12\sqrt{x^2 + y^2}\sqrt{(x-1)^2+y^2} \\ x^2 + y^2 - x = \tfrac12\sqrt{(x^2 + y^2)(x^2 + y^2 - 2x + 1); we square, which creates additional solutions where the angle is $120^\circ$ . Complete the square on the RHS: $(x^2 + y^2 - x)^2 = \tfrac14\left[(x^2 + y^2 - x)^2 + y^2\right].$ Subtract RHS from LHS and multiply the entire equation by $4/3$ : $(x^2 + y^2 - x)^2 - \frac13 y^2 = 0; \\ (x^2 + y^2 - x)^2 - \left(\frac1{\sqrt 3} y \right)^2 = 0; \\ \left(x^2 + y^2 - x - \frac1{\sqrt 3} y\right) \left(x^2 + y^2 - x + \frac1{\sqrt 3} y\right) = 0.$ This gives two solutions, corresponding to points above and below the square: $x^2 + y^2 - x \pm \frac1{\sqrt 3} y = 0;$ complete the square: $\left(x - \frac12\right)^2 + \left(y \pm \frac 1{2\sqrt 3}\right)^2 = \left(\frac 1{\sqrt 3}\right)^2.$ These are the equations of two circles, each with radius $\tfrac 1{\sqrt 3}$ , and centered at $(\tfrac12, \mp \tfrac1{2\sqrt 3})$ .

The solution follows from here...

---

Clearly, the geometric consideration of angles and arcs is a lot faster here. However, the vector approach leads to a great exercise in manipulating quartic polynomials, and algebraic geometry in general. Cheers!

A reply to the the challenge extra about the area swept out by the apex of a tetrahedron. (Being done as solution so I can use Latex).

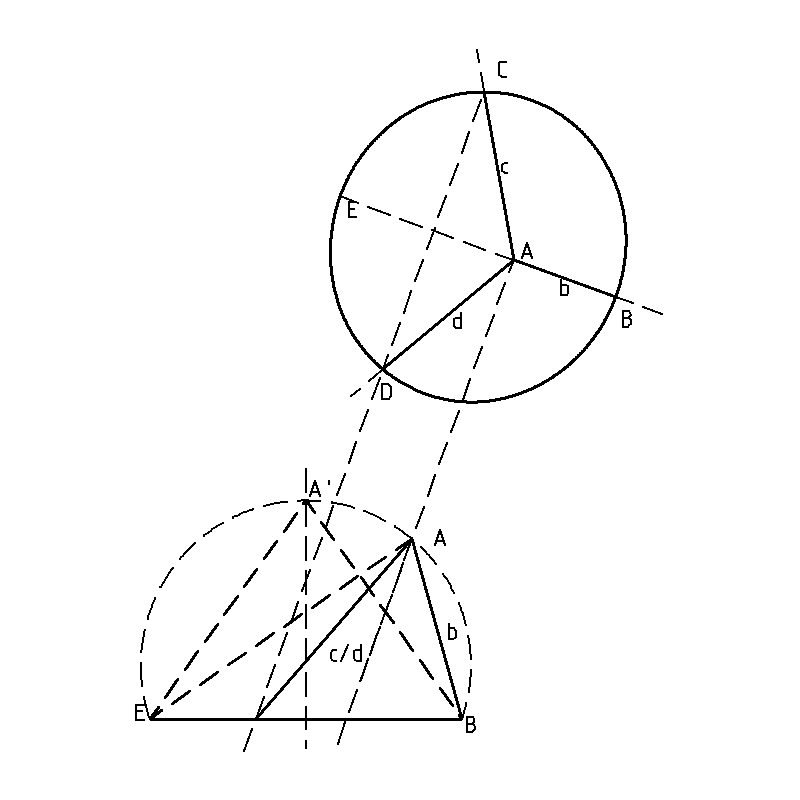
Essentially there are two parts to the answers firstly to show the 3D analogy to question is in fact a sphere and secondly the actual numbers.

Firstly the regular tetrahedron having apex A (in diagram) will have an angle of $arcsin({\frac{1}{\sqrt(3)}})$ about 35.3 degrees between the axis from its apex to the center of its base plane and any of the three edges (b,c or d). We could go through this but it is relatively straight forward 3D geometry. We will call this axis shown as A-A in diagram just "the axis" from now on.

The lower part of the diagram shows in elevation the tetrahedron in a general position. Whilst the upper part of the diagram shows the view looking down the axis towards the unit circle, which is shown as elliptical.

The first point is to note that the were you to spin the regular tetrahedron about the axis then any of the edges (b,c or d) will sweep out and generate the surface of of a right circular cone, its tip is shown in elevation as EAB. The edges will contact the unit circle at point B,C and D; at some point during the rotation one of the edges will be at point E. The ellipse containing points BCD &E is in fact the conic section, of the plane containing the unit circle, with the enclosing cone of the tetrahedron. During the rotation the Apex A will remain stationary. This means that point A is unique for any given axis direction. Thus the locus of A is the locus of the tip of a triangle EAB with constant $\angle{EAB} = 2 arcsin({\frac{1}{\sqrt(3)}})$ . The locus of such a triangle, in general, has been shown in the other solutions to be a circular arc. This is shown in the diagram as an arc containing EA'AB.

Without loss of generality the locus of A will be same arc no matter in which direction the axis is lying. Thus the loci of the Apex A is a partial sphere .

The second part is the numerical calculation: 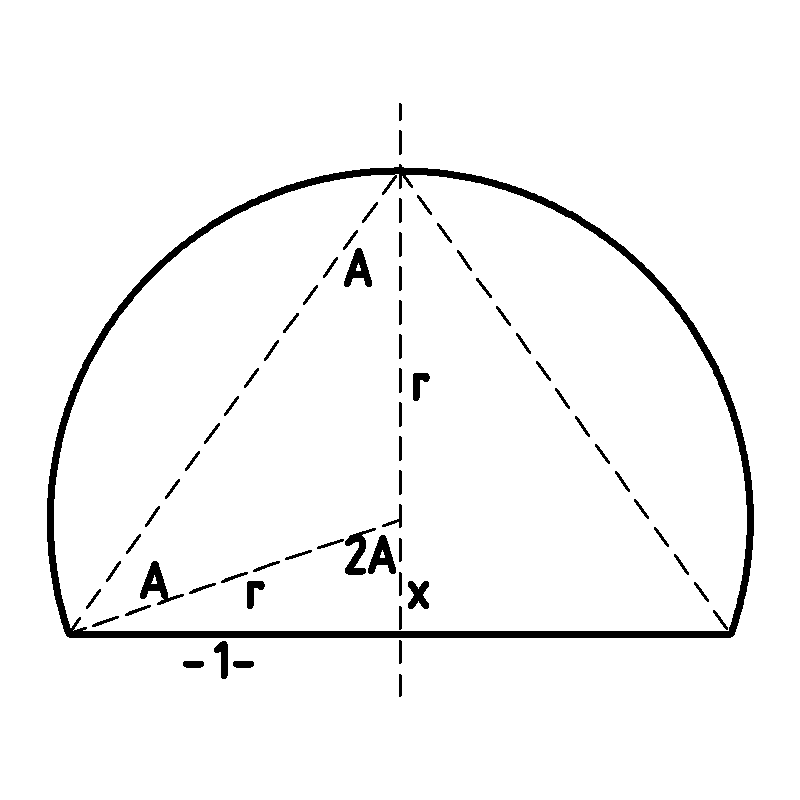Angle A is the semi angle of the enclosing cone namely $arcsin(\frac{1}{\sqrt 3})$

From the diagram using the double angle theorem and trig identities we have

$x = r cos(2A)$ = $r(1-2sin^2A)$ = $\frac {r}{3}$

Similarly r = $\frac{1}{cos(2A)}$ = $\frac{1}{2sin(A)cos(A)}$ = $\frac{1}{2} \cdot \frac {\sqrt3}{1} \cdot \frac{\sqrt3}{\sqrt2}$ = $\frac{3}{\sqrt8}$

The Area of a partial sphere is $2 \pi r (r+x)$ = $2 \pi \frac{3}{\sqrt8} \cdot \frac{4}{3} \cdot \frac {3}{\sqrt8}$ = $3\pi \approx$ 9.425

This is the result for the unit radius circle but the result for a unit diameter circle, more in keeping with the 2D question, will be $\frac{1}{4}$ of this $\approx$ 2.356 .

Let coordinates of point C be (x,y). If angle between the lines AC and BC is 60degrees then we can always complete an equilateral triangle. Slope of AC $=\frac{y}{x}$ Slope of BC $=\frac{y}{x-1}$

$\tan\frac{\pi}{3}=\frac {\frac{y}{x-1}-\frac{y}{x}}{1+(\frac{y}{x-1})(\frac{y}{x})}$ $\Rightarrow$ $(x-\frac{1}{2})^2+(y-\frac{1}{2\sqrt{3}})^2=\frac{1}{3}$ Thus,the locus of C turns out to be a circle for which minor arc AB subtends an angle of 120 degrees at the centre. But x,y are positive so we need the length of major arc AB,which is $\frac{1}{\sqrt{3}}.(4\pi)/3=2.418$